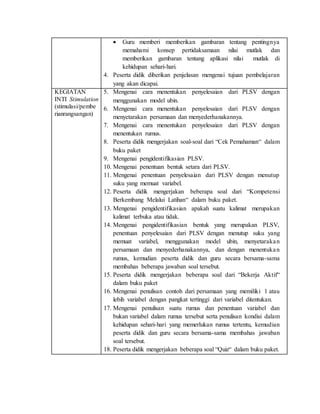
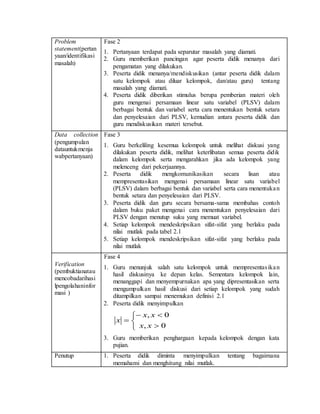
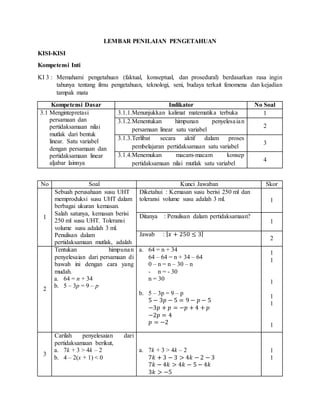
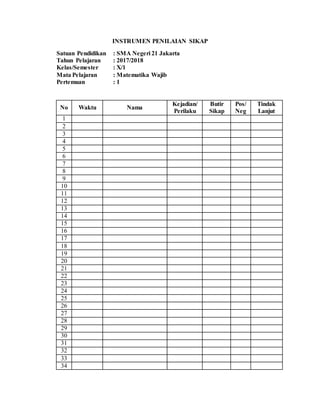
1. Rencana pelaksanaan pembelajaran (RPP) ini membahas pembelajaran materi persamaan dan pertidaksamaan nilai mutlak linear satu variabel untuk kelas X semester 1 di SMA Negeri 21 Jakarta. 2. Pembelajaran dilaksanakan selama 4 pertemuan dengan metode discovery learning dan diskusi kelompok serta pendekatan saintifik. 3. Tujuan pembelajaran adalah agar siswa dapat memahami konsep persamaan dan pertidaksamaan nilai mutlak satu variabel