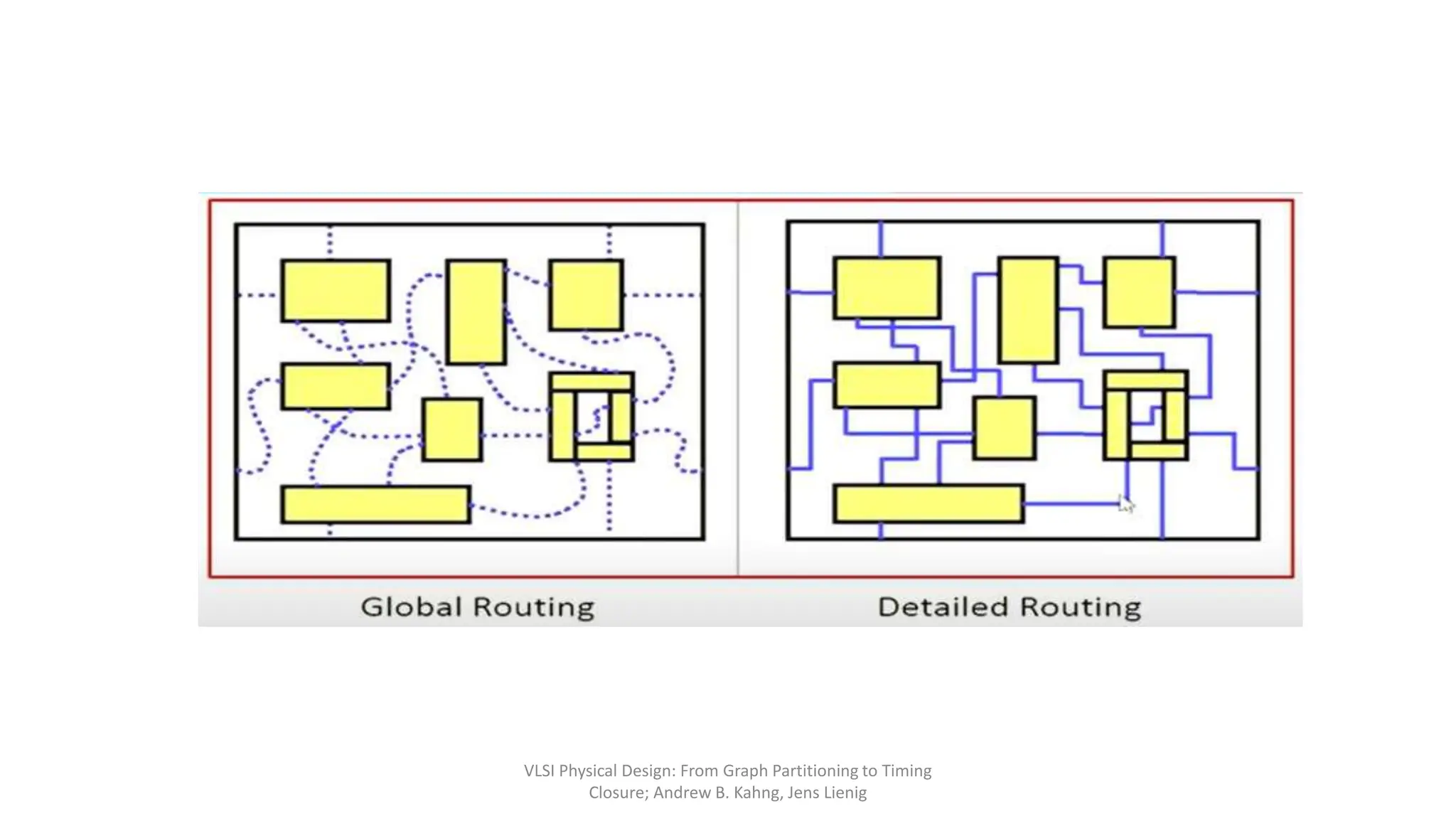
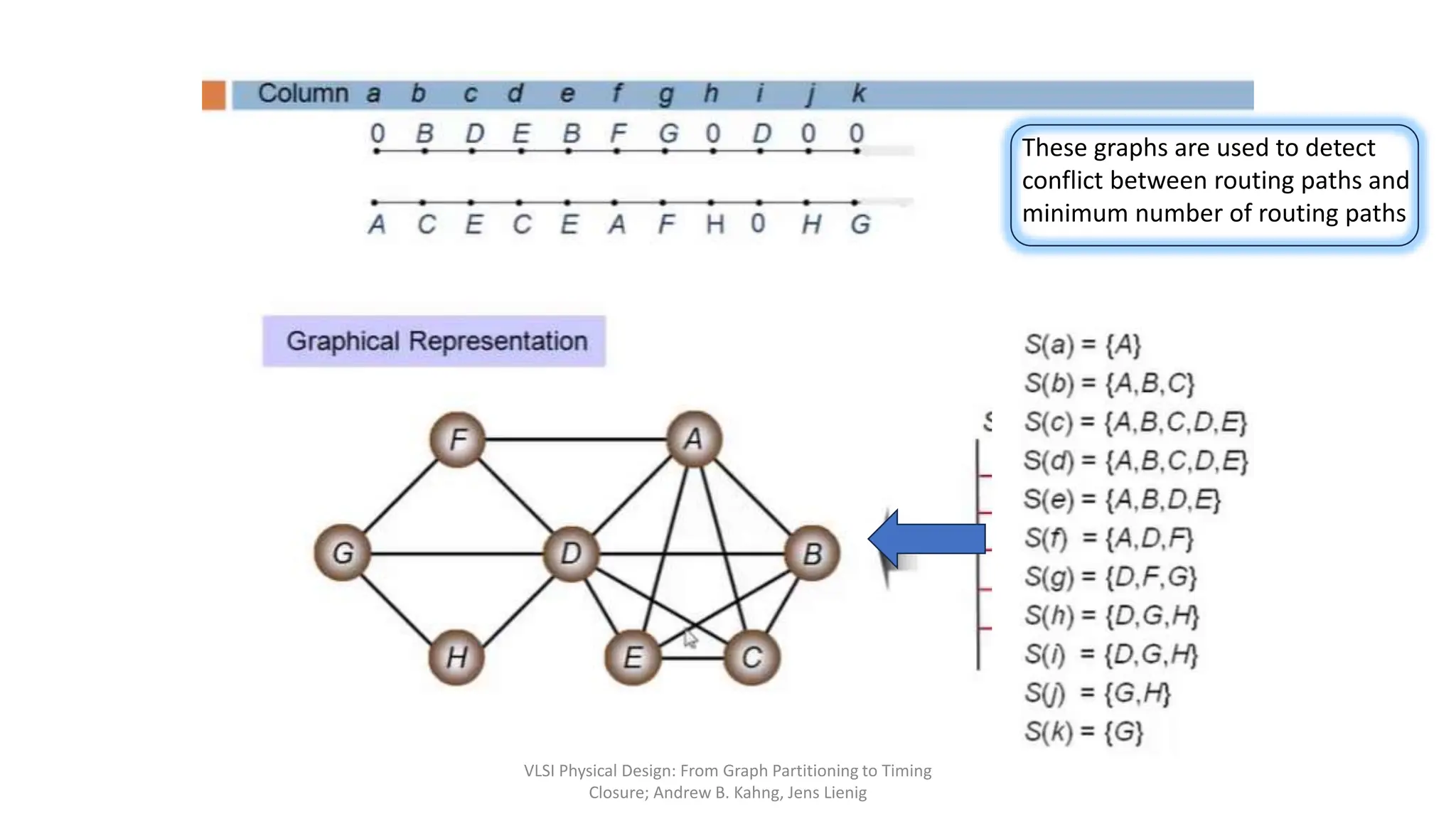
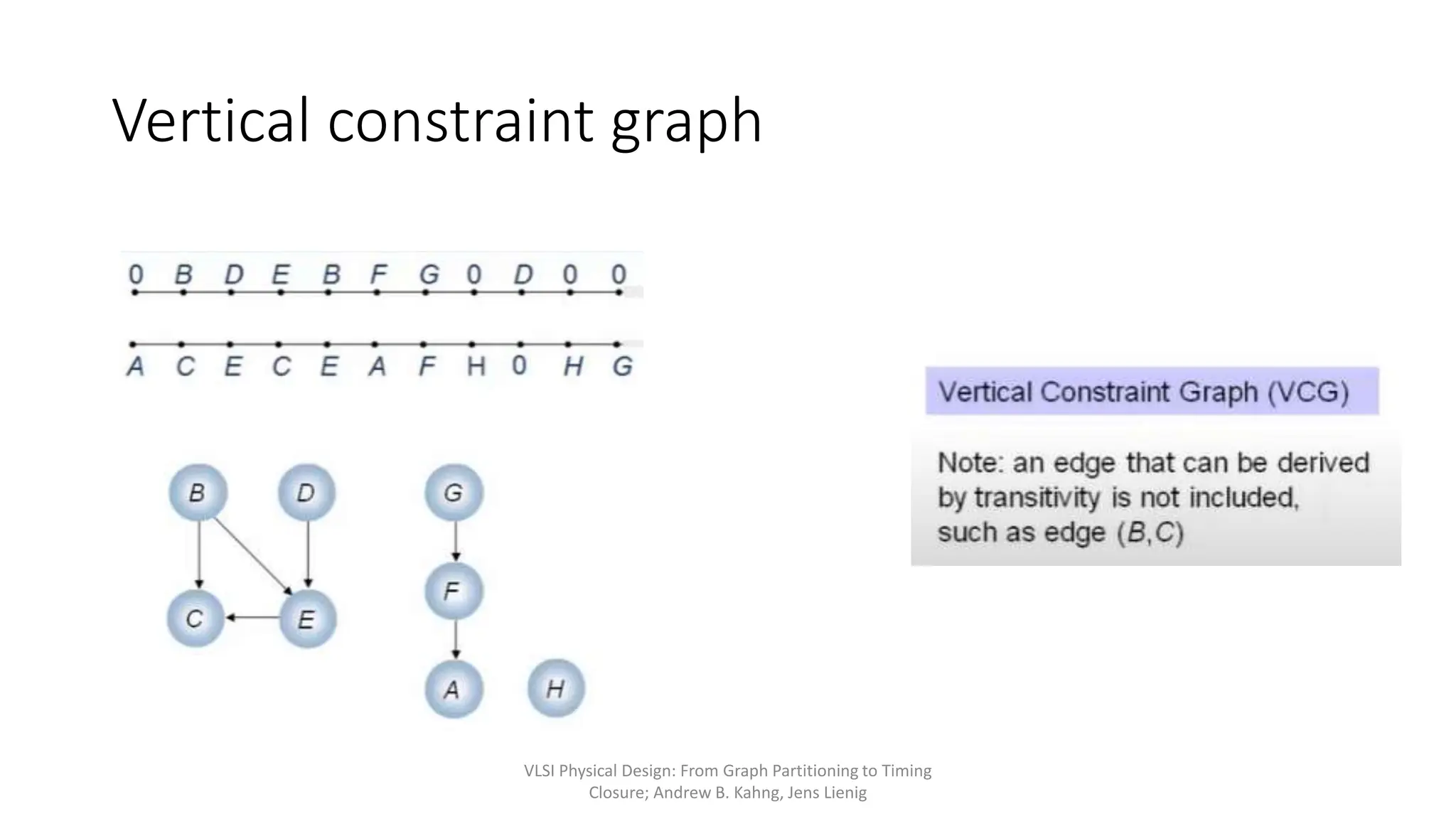
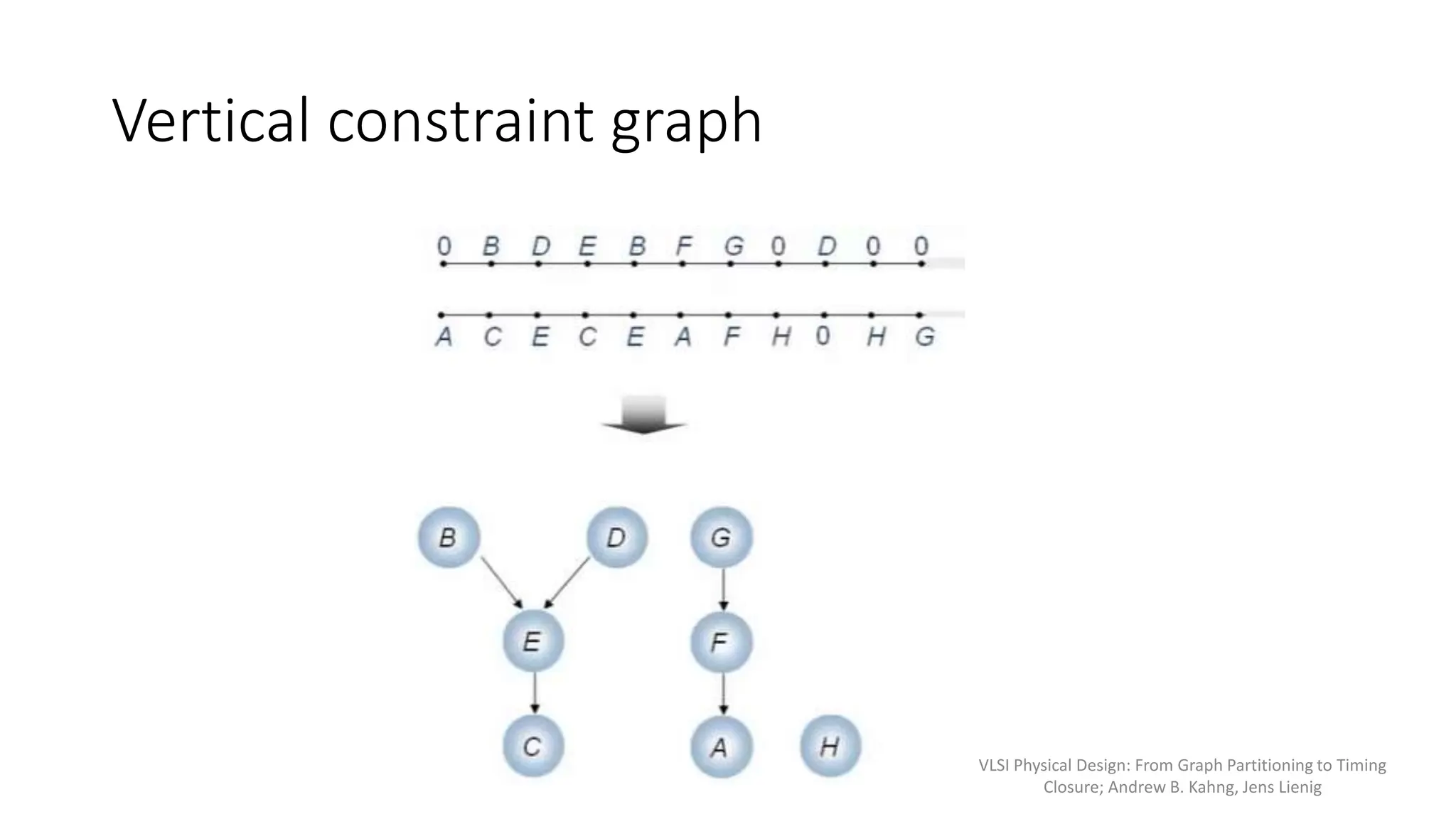
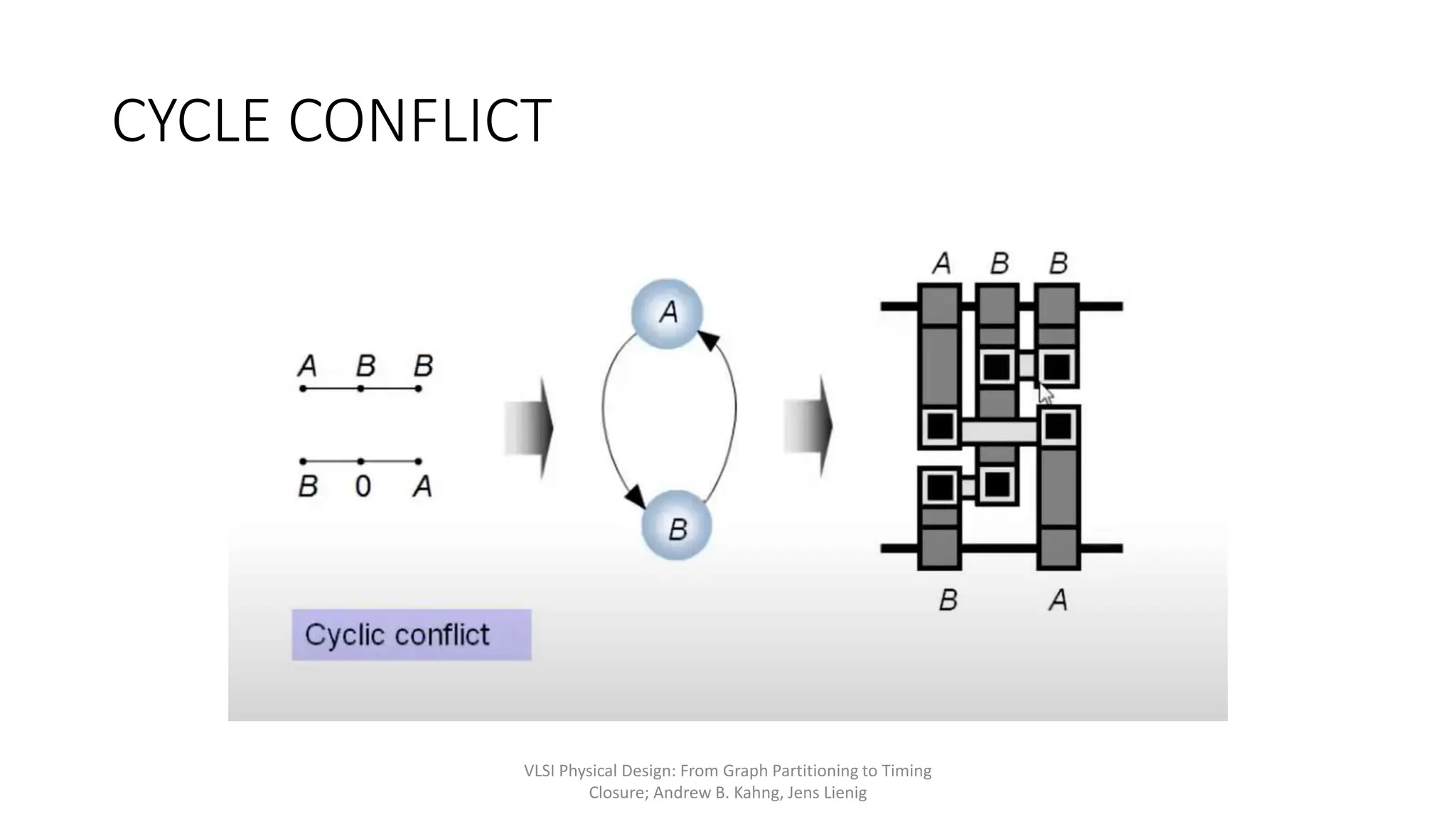
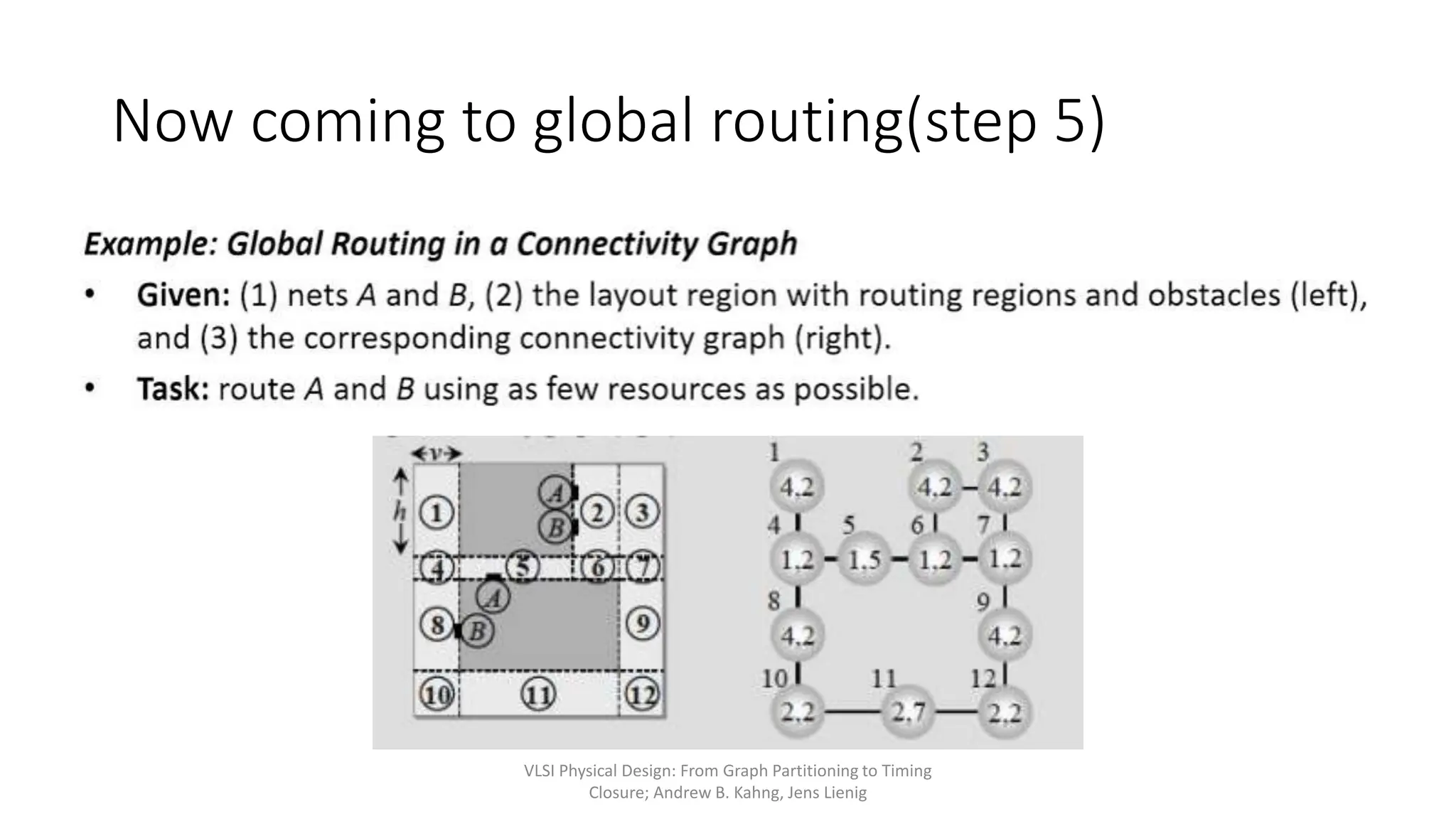
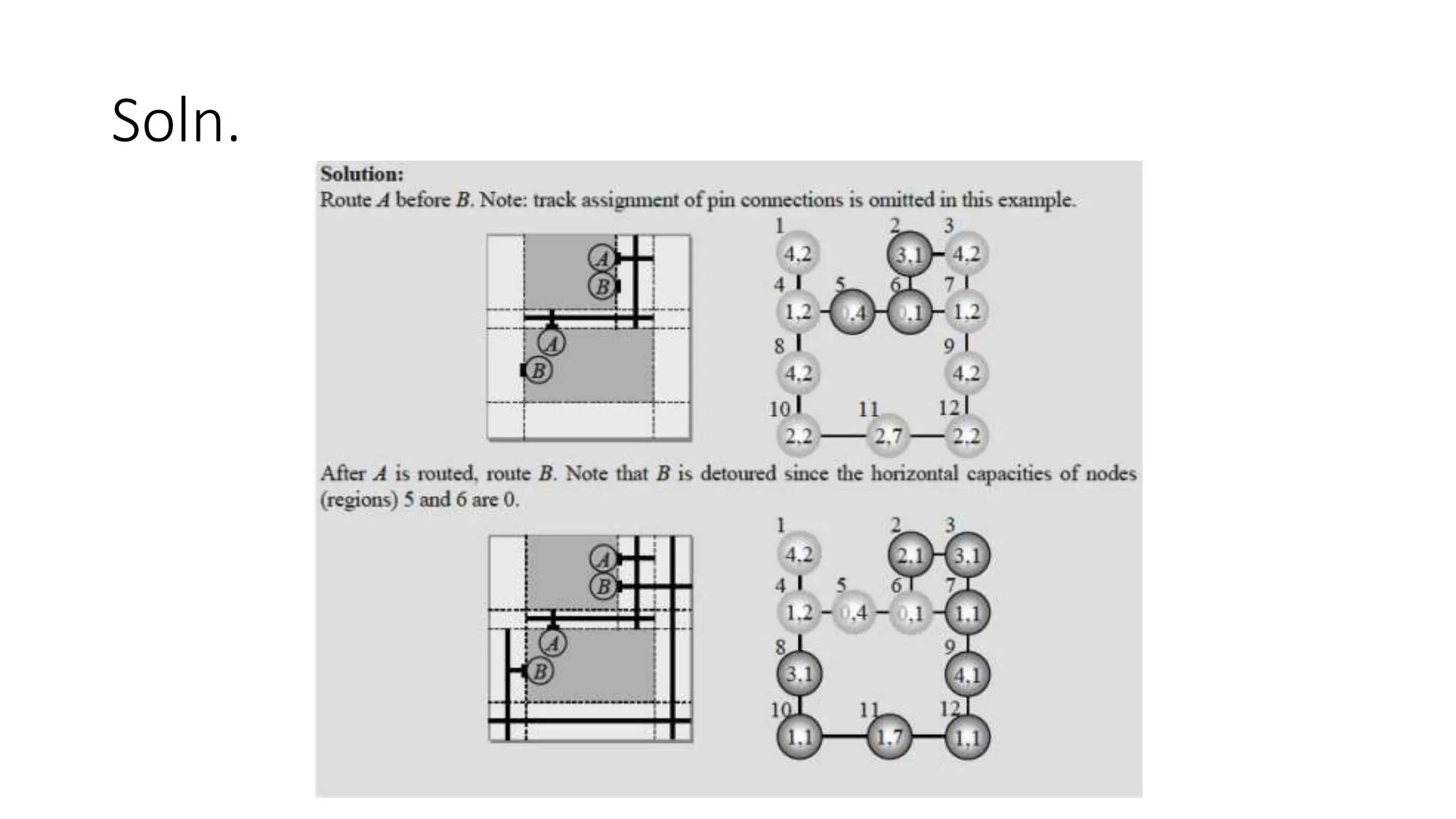
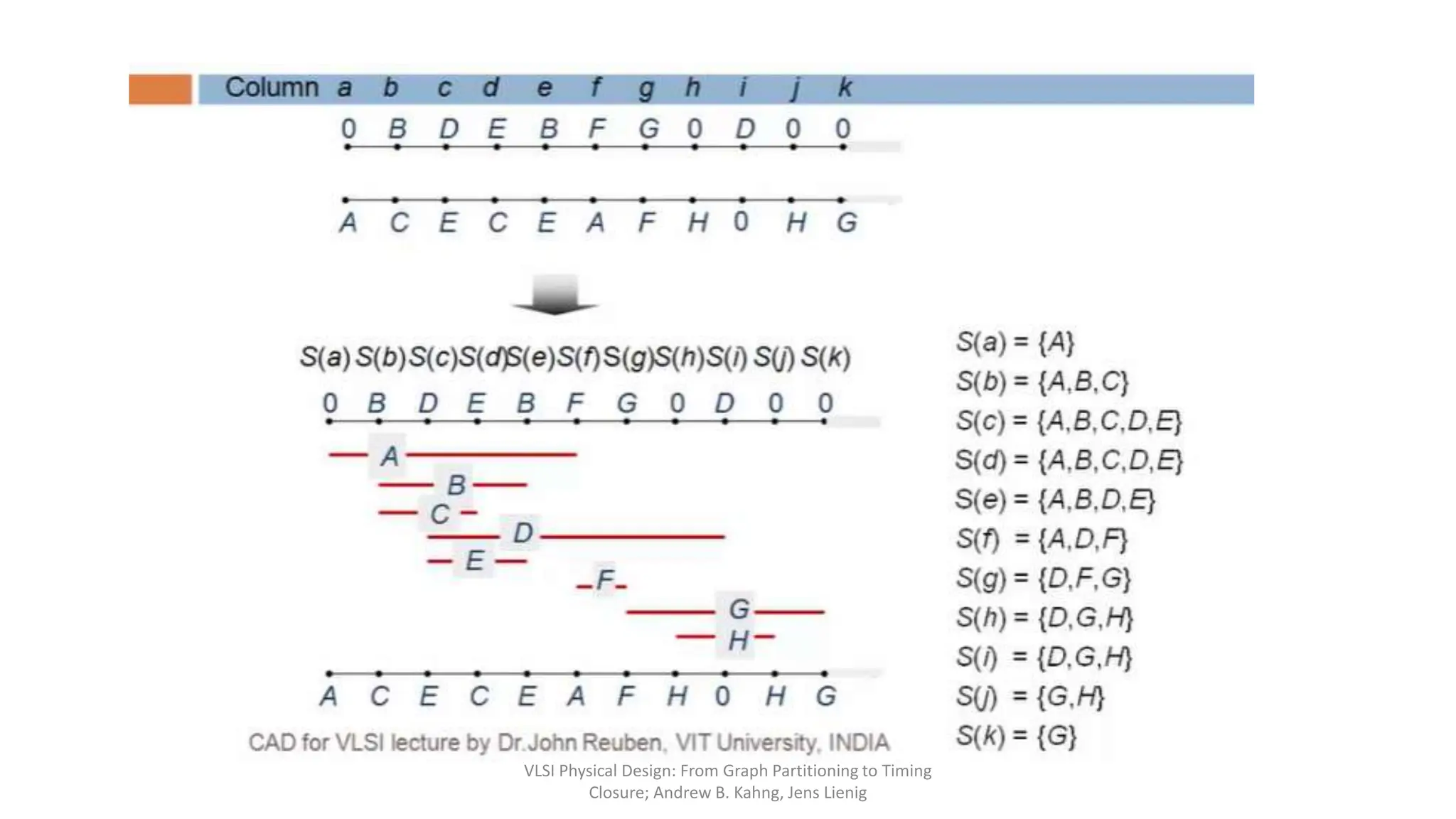
1) Global routing assigns nets to metal layers and routing cells in an approximate manner, while detailed routing decides the physical interconnections by allocating wires and vias. 2) Global routing seeks to determine if a placement is routable and finds a coarse routing for all nets within available regions. 3) Integer linear programming formulations model routing as a set of linear constraints and objectives and find optimal integer solutions for variable assignments.

1. Routing and Algorithms
By Prateek Tripathi
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

2. Basic Idea
• Global Routing: Global routes assign nets to particular metal
layers and global routing cells.in an approximate manner.
• Detailed Routing: For detailed routing, the router decides the
actual physical interconnections of nets by allocating wires on
each metal layer and vias for switching between metal layers.
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

3. VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

4. Some points to remember
• Vertical and horizontal tracks are laid out on different layers
• The junctions are connected by a “via”.
• There can be multiple layers of tracks depending upon the complexity
of the routing problem.
• As a conventional routing method we label the two or more pins with
the same name to specify the program that a connection is to be form
between them.
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

5. Optimization goal of Global Routing
• Seeks to determine whether a given placement is routable
• Seeks to determine a coarse routing for all nets within available
routing regions.
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

6. Grid Graph Model Illustration
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

7. Channel connectivity graph
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig
1. For horizontal channel, draw a line
parallel to x-axis along the block edges which
are parallel to x-axis, unless stopped by a
block.
2. For vertical channel, draw a line
parallel to y-axis along the block edges which
are parallel to y-axis., unless stopped by a
block.

8. Switch-box
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

9. Single net routing(rectilinear routing)
then the tree is a rectilinear minimum spanning
tree(RMST)
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

10. Further points
• The total edge length LRSMT of the RSMT is at least half the perimeter of the
minimum bounding box of the net:
LRSMT >= LMBB/2
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

11. VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

12. Hanan grid
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig
• For each points draw a lines perpendicular to y and x axis which passes through
the points
• Mark all the intersections of those lines as Hannan points

13. A sequential steiner tree heuristic
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig
T: Tree

16. VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

17. Steps to global routing in connectivity graph
• 1. Define the routing regions
• 2. Define the connectivity graph
• 3. Determine the net order(can be prioritised based on no. of pins, criticality, size of bounding box)
• 4. Assigning tracks for all pin connections(for each pin a horizontal and a vertical track are
reserved)
• 5. Global routing of all nets
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

19. Step 1
Step 2

20. Illustration of assigning capacities to the nodes
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

22. Final graph for previous slide
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

23. Now coming to global routing(step 5)
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

24. Soln.

25. Try yourself

26. Routing by Integer Linear Programming
• A linear program of a set of constraints and an optional objective
function.
• Objective function is maximised or minimised
• Constraints and objective must be linear.
• Constraints form a system of linear equation and inequalities
• An ILP is a linear program where every variable assume integer value.
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

27. Routing by Integer Linear Programming
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

28. VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

29. Horizontal Constraint Graph
Draw all the horizontal
Connections, each on a
Single line

30. VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

31. These graphs are used to detect
conflict between routing paths and
minimum number of routing paths
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

32. Vertical constraint graph
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

33. Vertical constraint graph
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

34. Vertical constraint graph
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

35. CYCLE CONFLICT
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

36. Left edge algorithm
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

37. Left edge algorithm
Soln.
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

38. Soln continued
From horizontal constraint graph we figured
out that we need at least 5 tracks
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

39. Final soln.
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

40. Dogleg algorithm
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

41. Dogleg Algorithm
• After splitting of the net, it follows the left edge algorithm
Example: Solve the given
figure with dogleg algorithm
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

42. Solution
VLSI Physical Design: From Graph Partitioning to Timing
Closure; Andrew B. Kahng, Jens Lienig

43. END