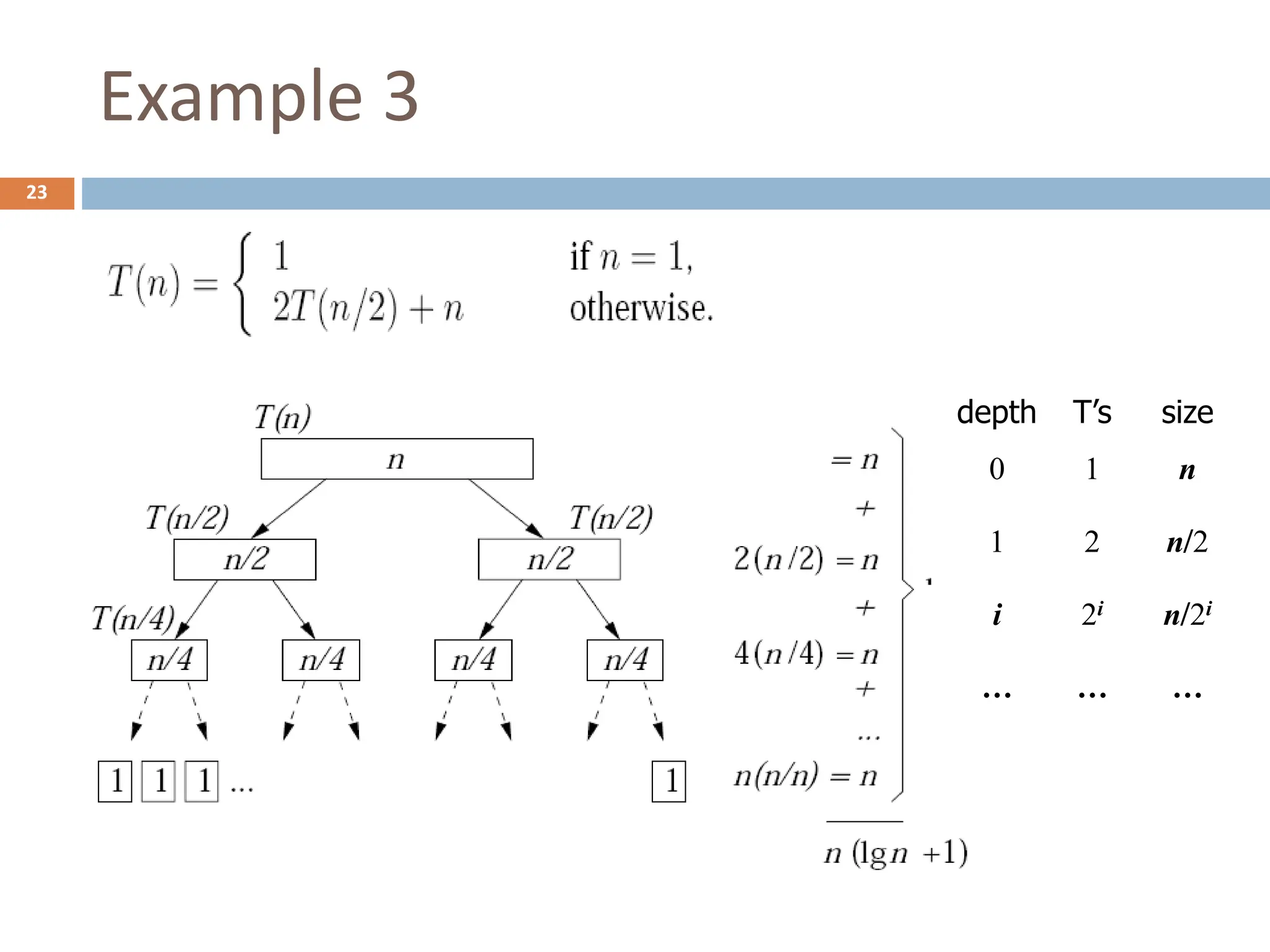
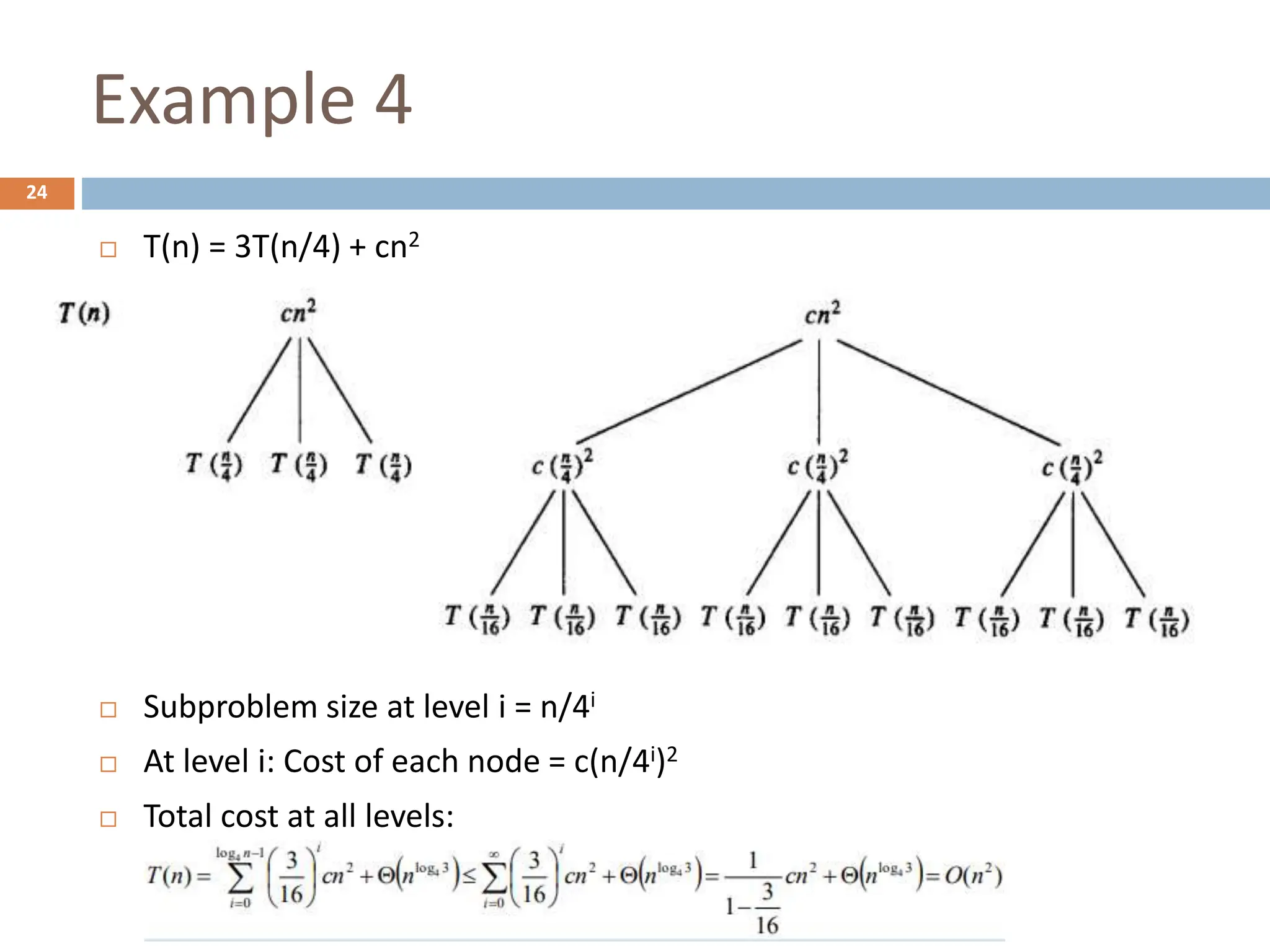
The document discusses recursion, which is a method for solving problems by breaking them down into smaller subproblems. It provides examples of recursive algorithms like summing a list of numbers, calculating factorials, and the Fibonacci sequence. It also covers recursive algorithm components like the base case and recursive call. Methods for analyzing recursive algorithms' running times are presented, including iteration, recursion trees, and the master theorem.

1. RECURSION

2. What is Recursion?
2
 Too big problems are too difficult to solve.
 Such problems can be broken down into sub-
problems and find a way to solve these sub-
problems.
 Results of these sub-problems are then combined
together to find the final solution.
 Recursion means "defining a problem in terms of
itself". It is the process of defining a problem in
terms of (a simpler version of) itself.

3. Parts of a Recursive Algorithm
3
 All recursive algorithms must have the following:
1) Base Case -when to stop- (is the solution to the
"simplest" possible problem).
2) Work toward Base Case (is where we make the
problem simpler).
3) Recursive Call (is where we use the same algorithm to
solve a simpler version of the problem).

4. Examples
4
 Summing a list of numbers:
 Factorial:
 Fibonacci:
sumList 𝐴, 𝑛 =
0 𝑖𝑓 𝑛 = 0
𝐴 𝑛 − 1 + sumList 𝐴, 𝑛 − 1 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
𝐹𝑎𝑐𝑡 𝑛 =
1 𝑖𝑓 𝑛 ≤ 1
𝑛. 𝐹𝑎𝑐𝑡 𝑛 − 1 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
fib 𝑛 =
1 𝑖𝑓 𝑙𝑜𝑐 < 2
𝑓𝑖𝑏 𝑛 − 1 + 𝑓𝑖𝑏 𝑛 − 2 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒

5. Cont.
5  Summing a list of numbers:
 Factorial:
 Fibonacci:
int sumA(A, n){
if(n == 0)
return 0;
else
return A[n-1] + SumA(A,n-1);}
int factorial(int n) {
if( n <= 1 )
return 1;
else
return n * factorial ( n – 1 );}
int Fibonacci (int n){
if(n < 2)
return 1;
else
return fibonacci(n - 1) + fibonacci(n - 2);}

6. Binary search Algorithm
 Binary search: for an ordered array A, finds if x is in the array A[lo…hi]
Alg.:BINARY-SEARCH (A, lo, hi, x)
if (lo > hi)
return FALSE
mid  (lo+hi)/2
if x = A[mid]
return TRUE
if ( x < A[mid] )
BINARY-SEARCH (A, lo, mid-1, x)
if ( x > A[mid] )
BINARY-SEARCH (A, mid+1, hi, x)
12
11
10
9
7
5
3
2
1 2 3 4 5 6 7 8
mid
lo hi
T(n) = c + T(n/2)

7. Example
 A[8] = {1, 2, 3, 4, 5, 7, 9, 11}
 lo = 1 hi = 8 x = 7
7
mid = 4, lo = 5, hi = 8
mid = 6, A[mid] = x Found!
11
9
7
5
4
3
2
1
11
9
7
5
4
3
2
1
1 2 3 4 5 6 7 8

8. Example
8
• lo = 1 hi = 8 x = 6
mid = 4, lo = 5, hi = 8
mid = 6, A[6] = 7, lo = 5, hi = 5
11
9
7
5
4
3
2
1
11
9
7
5
4
3
2
1
1 2 3 4 5 6 7 8
11
9
7
5
4
3
2
1 mid = 5, A[5] = 5, lo = 6, hi = 5
NOT FOUND!

9. Recurrences and Running Time
9
 What is the actual running time of the algorithm?
 Need to solve the recurrence
 Find an explicit formula of the expression (the
generic term of the sequence)

10. Advantages and Disadvantages of Recursion
10
 Recursive solutions are much easier to conceive of
and code than their iterative counterparts.
 However, Every problem is not solvable using this
approach !!!
 What kinds of problems are solved with recursion?
 Generally, problems which are defined in terms of
themselves are usually good candidates for
recursive techniques.

11. Efficiency of Recursion
11
 Recursive method often slower than iterative; why?
 Overhead for loop repetition smaller than overhead for
call and return
 If easier to develop algorithm using recursion
 Then code it as a recursive method.
 Software engineering benefit probably outweighs ...
 Reduction in efficiency

12. Example Recurrences
12
 T(n) = T(n-1) + n Θ(n2)
 Recursive algorithm that loops through the input to eliminate one item
 T(n) = T(n/2) + c Θ(logn)
 Recursive algorithm that halves the input in one step
 T(n) = T(n/2) + n Θ(n)
 Recursive algorithm that halves the input but must examine every item
in the input
 T(n) = 2T(n/2) + 1 Θ(n)
 Recursive algorithm that splits the input into 2 halves and does a
constant amount of other work

13. Methods for solving recurrences
13
1. Iteration method: In the iterative substitution, or
“plug-and-chug” technique, we iteratively apply the
recurrence equation to itself and see if we can find
a pattern.
2. Recursion tree method: The recursion-tree method
converts the recurrence into a tree whose nodes
represent the costs incurred at various levels of the
recursion. We use techniques for bounding
summations to solve the recurrence.

14. Methods for solving recurrences
14
3. Master method: The Master method is a general method
for solving (getting a closed form solution to) recurrence
relations that arise frequently in divide and conquer
algorithms.

15. 1. The Iteration Method
15
Example: Give the complexity for T(n) = c + T(n/2)
T(n) = c + T(n/2)
= c + c + T(n/4)
= c + c + c + T(n/8)
= 3c + T(n/23)
….
= k.c + T(n/2k)
= k.c + T(n/n)
= clogn + T(1)
= Θ(logn)
-We know that T(1) = 1 the base case.
-In particular we want T(1) to appear on the
right hand side of the equation.
-This means we want:
n/2k = 1 => n = 2k => log n = k

16. Iteration Method – Example
16
Example: T(n) = n + 2T(n/2)
T(n) = n + 2T(n/2)
= n + 2(n/2 + 2T(n/4))
= n + n + 4T(n/4)
= n + n + 4(n/4 + 2T(n/8))
= n + n + n + 8T(n/8)
= 3n + 23T(n/23)
….
= kn + 2k T(n/2k)
= kn + n T(n/n)
= nlogn + nT(1) = Θ(nlogn)
-We know that T(1) = 1 the base case.
-In particular we want T(1) to appear on the
right hand side of the equation.
-This means we want:
n/2k = 1 => n = 2k => log n = k

17. Iteration Method – Example
17
Example: T(n) = n + T(n-1)
T(n) = n + T(n-1)
= n + (n-1) + T(n-2)
= n + (n-1) + (n-2) + T(n-3)
= n + (n-1) + (n-2) + … + 2 + T(1)
= n(n+1)/2 - 1 + T(1)
= Θ(n2)







n
k
n
k
1
...
2
1 n(n+1)/2

18. Iteration Method – Example
18
T(n) = n + 2T(n/2)
= n + 2(n/2 + 2T(n/4))
= n + n + 4T(n/4)
= n + n + 4(n/4 + 2T(n/8))
= n + n + n + 8T(n/8) Note n/8 = n/23
….
= kn + 2kT(n/2k)
= kn + 2kT(1)
= nlogn + nT(1)
= Θ(nlogn)
Example: T(n/2) = n/2 + 2T(n/4)
-We know that T(1) = 1 the base case.
-In particular we want T(1) to appear on the
right hand side of the equation.
-This means we want:
n/2k = 1 => n = 2k => log n = k

19. 2. The Recursion Tree
19
 Convert the recurrence into a tree:
 Each node represents the cost incurred at that level of recursion
 Sum up the costs of all levels
 For instance, consider the recurrence
T(n) = 2T(n/2) + n2

20. The Recursion Tree Cont.
20
 In this case, it is straightforward to sum across each row of
the tree to obtain the total work done at a given level:
 This is a geometric series, thus in the limit the sum is O(n2).
 The amount of work at each level is decreasing so quickly
that the total is only a constant factor more than the root.
n2
½ n2
¼ n2
1/8 n2
…

21. Cont.
 Subproblem size at level i is: n/2i
 Subproblem size hits 1 when 1 = n/2i  i = lg n
 Cost of the problem at level i = n2/2i,
 No. of nodes at level i = 2i
 Total cost:
 T(n) = O(n2)
21
2
2
0
2
1
lg
0
2
lg
1
lg
0
2
2
)
(
2
1
1
1
)
(
2
1
2
1
)
1
(
2
2
)
( n
n
O
n
n
O
n
n
n
W
n
n
W
i
i
n
i
i
n
n
i
i





















 









22. Example 2
22
 Solve T(n) = T(n/4) + T(n/2)+ n2

23. Example 3
23
depth T’s size
0 1 n
1 2 n/2
i 2i n/2i
… … …

24. Example 4
24
 T(n) = 3T(n/4) + cn2
 Subproblem size at level i = n/4i
 At level i: Cost of each node = c(n/4i)2
 Total cost at all levels:

25. 3. Master Theorem
25
 The Master Theorem applies to recurrences of the
following form:
𝑇 𝑛 = 𝑎𝑇
𝑛
𝑏
+ 𝑓 𝑛 𝑤ℎ𝑒𝑟𝑒 𝑎 ≥ 1 𝑎𝑛𝑑 𝑏 ≥ 2
 n is the size of the problem.
 a is the number of subproblems in the recursion.
 n/b is the size of each subproblem. (Here it is assumed that
all subproblems are essentially the same size.)
 f (n) is the cost of the work done outside the recursive calls,
which includes the cost of dividing and merging. (i.e., the
non-recursive time f(n) = Θ(nd))

26. Theorem
26

27. Example1
27
𝑎 < 𝑏𝑑

28. Example
28
𝑎 = 𝑏𝑑

29. Example
29

30. Master Theorem
30