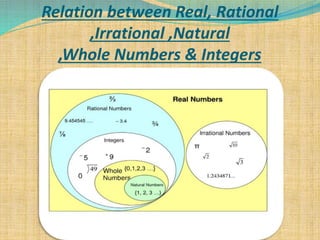
1. The document defines and provides examples of different types of numbers: natural numbers, whole numbers, integers, rational numbers, irrational numbers, and real numbers. 2. Key definitions include natural numbers being positive whole numbers starting at 1, whole numbers including zero, integers including positive and negative numbers on the number line, rational numbers being fractions, and irrational numbers being non-terminating and non-repeating numbers. 3. The document also presents the Fundamental Theorem of Arithmetic and Euclid's Division Lemma, with the former stating every composite number can be uniquely expressed as a product of prime numbers and the latter relating integers a and b using the division algorithm.

1. CH = 1

2. Natural Numbers
The positive counting numbers starting from 1 not
including zero are called Natural Numbers
These are denoted by ‘N’ Letter
21 22 23 24 ………. All are
Natural Numbers

3. Whole Numbers
All the natural numbers including zero [0] are called
Whole Numbers
These are denoted by letter ‘W’
10 11 12 ……
All are
Whole Numbers

4. Integers
All positive & negative numbers which can be
represented on number line are called Integers
We can say that integers are set of natural numbers &
their opposites & zero
These are denoted by letter ‘Z’
{…,-3, -2, -1, 0, 1, 2, 3,…}

6. Rational Numbers
q
p
The numbers which can be written in the form
where p & q are integers ; q ≠ 0
are called Rational numbers
They can be expressed as Terminating &
Non - Terminating Repeating Numbers
Examples -> 1. 56345467.39472348793
2. 90347809732.453653643
3. 3247034729387403847923748039247982374923
4. 6666.66 5. 0.00000000000003
6. 200 7. 19.1 ETC.
______________
___

7. Irrational Numbers
The Non Terminating & Non Repeating Numbers are
called Irrational Numbers
These Numbers cannot be expressed in the form
q
p
Examples ->
1. π 2. 1.01001001000……….
3. 5454.112123123412345……..
4. 74354354534.313323333343353363………
ETC.

8. Real Numbers
The sum of all Rational & Irrational numbers
is called Real Numbers
It is denoted by letter ‘R’

9. Relation between Real, Rational
,Irrational ,Natural
,Whole Numbers & Integers

11. Fundamental Theorem Of
Arithmetic (FTA)
This States That ->
‘ Every Composite No. can be expressed as product of its
prime numbers and this expression is unique , apart
from the order in which prime factors occur ’

13. Euclid’s Division Lemma
It states that ->
‘ For any 2 positive integers a & b there exists 2 unique
integers q & r which satisfies that ->
a = b*q + r , 0 < r < b & b < a ’__

15. Prepared By ->
BHAVYAM ARORA
Class = Tenth ‘A’
Roll No. = 37