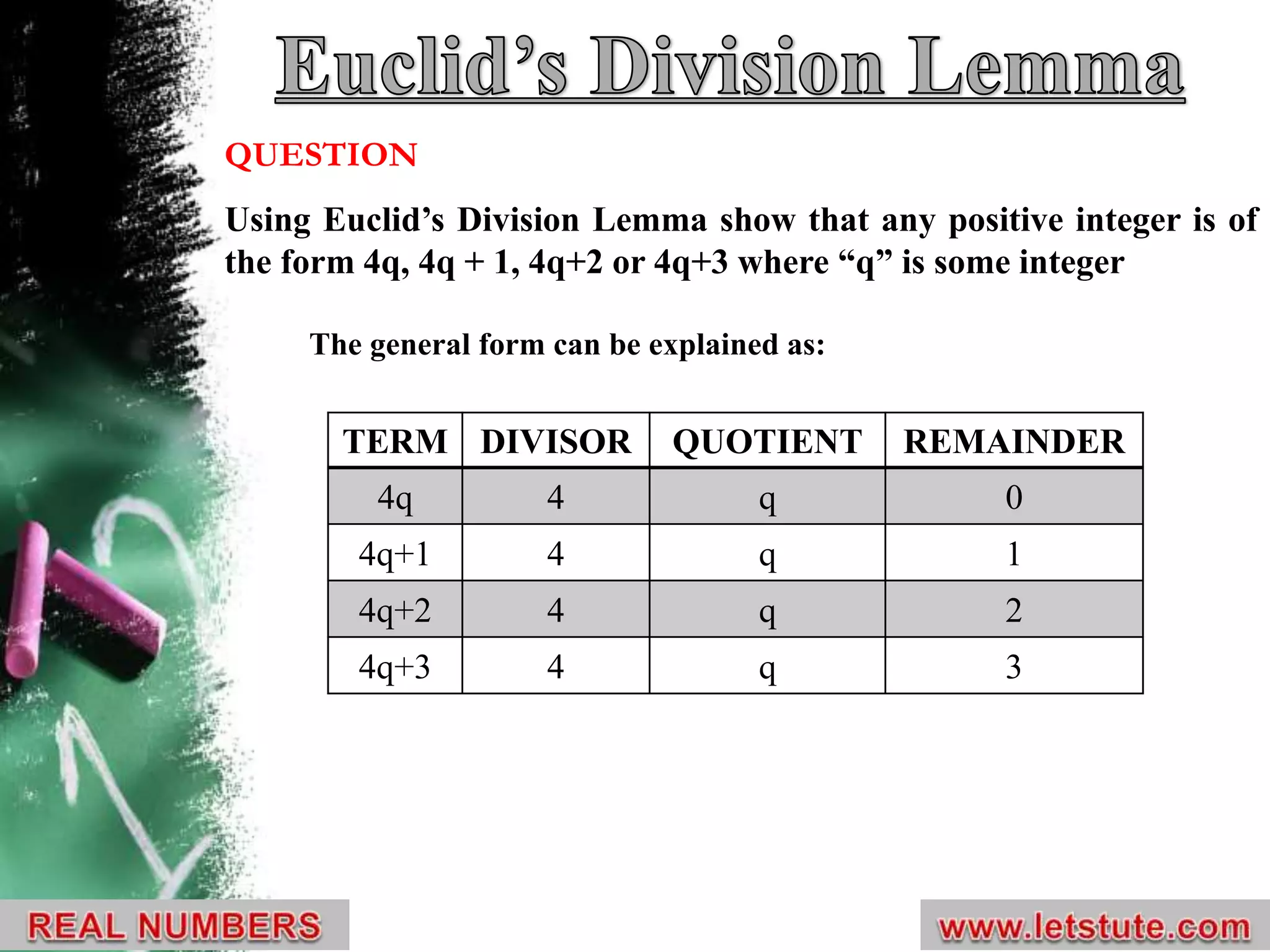
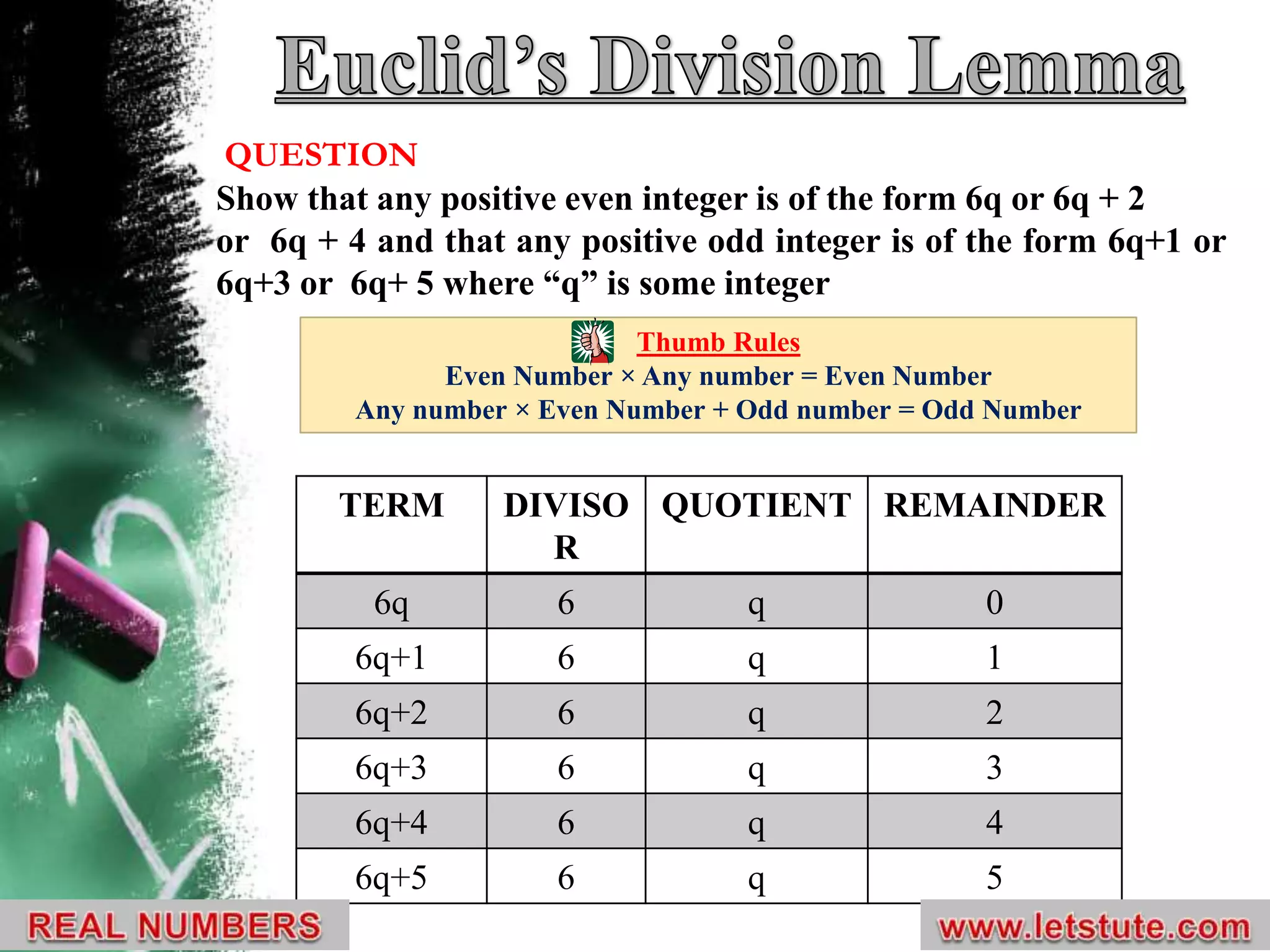
The document explains Euclid's division lemma and demonstrates how any positive integer can be expressed in specific forms based on its division by 4 and 6. It further shows that positive even integers can be expressed as 6q, 6q + 2, or 6q + 4, while positive odd integers can be expressed as 6q + 1, 6q + 3, or 6q + 5. Additionally, it establishes that the square of any positive integer is represented as 4p or 4p + 1, and specifically for odd integers, the form is 8m + 1.

2. a = b × q + r
0 ≤ r < b
The general equation can be represented as:
Where:
a = Dividend, b= Divisor, q = Quotient, r = Remainder

3. Using Euclid’s Division Lemma show that any positive integer is of
the form 4q, 4q + 1, 4q+2 or 4q+3 where “q” is some integer
The general form can be explained as:
TERM DIVISOR QUOTIENT REMAINDER
4q 4 q 0
4q+1 4 q 1
4q+2 4 q 2
4q+3 4 q 3
QUESTION

4. SOLUTION
Let ‘a’ be any positive integer
On dividing “a” by 4 , let “q” be the quotient and “r” be the remainder
Then, by Euclid’s Division Lemma, we have:
(a = b × q + r)
a = 4q + r , where 0 ≤ r < 4
 a = 4 q + r , where r = 0, 1, 2 or 3
 a = 4q ( when r = 0)
 a = 4q + 1 ( when r = 1)
 a = 4q + 2 ( when r = 2)
 a = 4q + 3 ( when r = 3)
 Any positive integer is of the form 4q, 4q + 1, 4q+2 or 4q+3

5. Show that any positive even integer is of the form 6q or 6q + 2
or 6q + 4 and that any positive odd integer is of the form 6q+1 or
6q+3 or 6q+ 5 where “q” is some integer
Thumb Rules
Even Number × Any number = Even Number
Any number × Even Number + Odd number = Odd Number
TERM DIVISO
R
QUOTIENT REMAINDER
6q 6 q 0
6q+1 6 q 1
6q+2 6 q 2
6q+3 6 q 3
6q+4 6 q 4
6q+5 6 q 5
QUESTION

6. Let “a” be any positive integer
On dividing “a” by 6 , let “q” be the quotient and “r” be the remainder.
Then , by Euclid’s Division Lemma, we have
a = 6q + r , where 0 ≤ r < 6
a = 6q + r , where “r” = 0, 1, 2 , 3 , 4, or 5
Positive even integers Positive odd integers
a = 6q (where r = 0) a = 6q + 1 ( where r = 1)
a = 6q + 2 ( where r = 2) a = 6q + 3 ( where r = 3)
a = 6q + 4 ( where r = 4) a = 6q + 5 ( where r = 5)
SOLUTION
 Any positive even integer is of the form 6q or 6q + 2 or 6q + 4 and that
any positive odd integer is of the form 6q+1 or 6q+3 or 6q+ 5 where “q”
is some integer

7. Case 1 Case 2
If “m” is Even If “m” is Odd
when m = 2q when m= 2q + 1
m2 = (2q)2 m2 = (2q + 1) 2
m2 = 4q2 m2= 4q2 + 4q + 1
m2 = 4q(q+0) m2 = 4q(q+1) + 1
m2 = 4p {p= q(q+0) } m2 = 4p +1 {p= q(q+1 )}
QUESTION
Show that the square of any positive integer is of the form 4p or
4p+1 for some integer “p”
SOLUTION
Let ‘ m’ be the positive integer
The square of any positive integer is of the form 4p or 4p + 1 for
some integer “p”

8. On dividing a by 8 , let “q” be the quotient and “r” be the
remainder
Then , by Euclid’s Division Lemma, we have
a = 8q + r , where 0 ≤ r < 8 (r = 0,1,2,3,4,5,6 or 7)
 We want only positive odd integers, we will consider only the odd
values of ‘r’ which are
a= 8q +1,
a= 8q+3,
a= 8q + 5 or
a= 8q + 7
QUESTION
Show that the square of any positive odd integer is of the form
8m + 1 for some integer “m”
SOLUTION
Let ‘a’ be any positive odd integer

9. Case 1
when a = 8q + 1
a2 = (8q + 1)2
a2 = 64 q2 +16 q + 1
a2 = 8q(8q+2) + 1
a2 = 8m + 1 {m= q(8q+2)}
Case 2
when a = 8q + 3
a2 = (8q + 3)2
a2 = 64 q2 +48 q + 9
a2 = 64 q2 +48 q + 8 + 1
a2 = 8(8q2 +6q + 1 ) + 1
a2 = 8m + 1 {m = (8q2 +6+1)}
Case 3
when a = 8q + 5
a2 = (8q + 5)2
a2 = 64 q2 +80 q + 25
a2 = 64 q2 +80 q + 24 + 1
a2 = 8(8 q2 +10 q + 3) + 1
a2 = 8m + 1
{m= (8q2 +10q+1)}
Case 4
when a = 8q + 7
a2 = (8q + 7)2
a2 = 64 q2 +112 q + 49
a2 = 64 q2 +112 q + 48 + 1
a2 = 8(8 q2 +14 q + 6) + 1
a2 = 8m + 1{m= (8q2 + 14q+6)}
The square of any positive odd integer is of the form 8m + 1 for
some integer “m”

10. 1. Arranging the terms in the given question as per the Euclid’s
Division Lemma
2. Identification of the Dividend, Divisor, Quotient and Remainder .
3. Any positive integer can be represented as ‘2q’ or ‘2q+1’.
4. Even number × Any Number = Even number .
5. Even number × Any Number + Odd number = Odd number .
a = b × q + r
REVISION
General equation