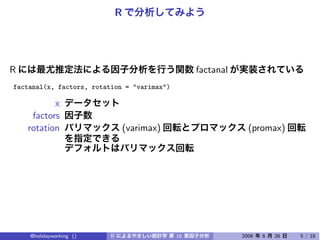
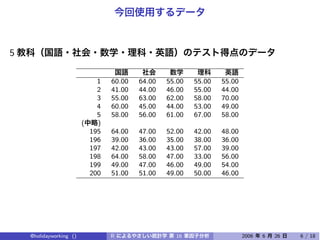
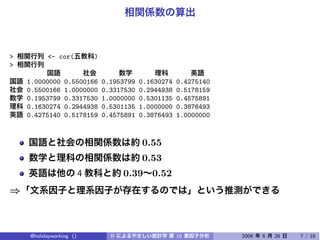
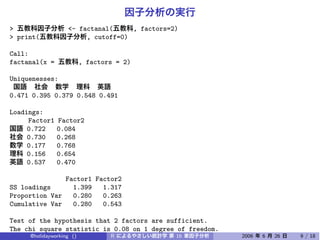
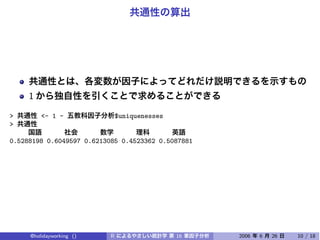
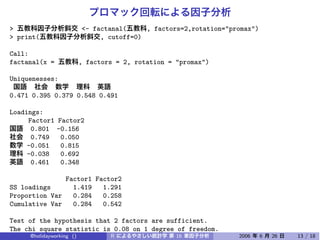
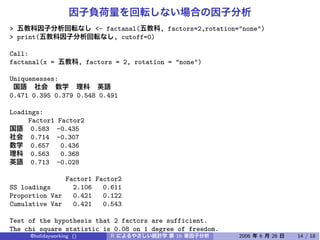
The document discusses using factor analysis to analyze a dataset with 5 variables and 200 observations. It performs factor analysis with 2 factors using varimax rotation and promax rotation. It also examines the unrotated factor solution. The analysis finds that 2 factors explain 54.3% of the total variance in the variables.

1. R 16
@holidayworking
2006 6 26
@holidayworking () R 16 2006 6 26 1 / 18

2. 1
2
3 R
@holidayworking () R 16 2006 6 26 2 / 18

3. )
Twitter: @holidayworking
:
:
: T-SQUARE F1
:
Java, PL/SQL:
Python, Ruby:
@holidayworking () R 16 2006 6 26 3 / 18

4. i i i i
:
5
@holidayworking () R 16 2006 6 26 4 / 18

5. R
R factanal
factanal(x, factors, rotation = "varimax")
x
factors
rotation (varimax) (promax)
@holidayworking () R 16 2006 6 26 5 / 18

6. 5
1 60.00 64.00 55.00 55.00 55.00
2 41.00 44.00 46.00 55.00 44.00
3 55.00 63.00 62.00 58.00 70.00
4 60.00 45.00 44.00 53.00 49.00
5 58.00 56.00 61.00 67.00 58.00
( )
195 64.00 47.00 52.00 42.00 48.00
196 39.00 36.00 35.00 38.00 36.00
197 42.00 43.00 43.00 57.00 39.00
198 64.00 58.00 47.00 33.00 56.00
199 49.00 47.00 46.00 49.00 54.00
200 51.00 51.00 49.00 50.00 46.00
@holidayworking () R 16 2006 6 26 6 / 18

7. > <- cor( )
>
1.0000000 0.5500166 0.1953799 0.1630274 0.4275140
0.5500166 1.0000000 0.3317530 0.2944938 0.5178159
0.1953799 0.3317530 1.0000000 0.5301135 0.4575891
0.1630274 0.2944938 0.5301135 1.0000000 0.3876493
0.4275140 0.5178159 0.4575891 0.3876493 1.0000000
0.55
0.53
4 0.39 0.52
⇒
@holidayworking () R 16 2006 6 26 7 / 18

8. 1
> eigen( )
$values
[1] 2.5573782 1.0656034 0.5058941 0.4461472 0.4249772
$vectors
[,1] [,2] [,3] [,4] [,5]
[1,] -0.4040025 0.57915506 -0.3526733 -0.30988872 0.53004894
[2,] -0.4791362 0.36314955 -0.1046695 0.07323541 -0.78881668
[3,] -0.4380493 -0.48395278 0.2494573 -0.71311577 -0.05603054
[4,] -0.4064807 -0.54402387 -0.6062633 0.39786745 0.11383232
[5,] -0.5000967 0.05029462 0.6594556 0.48142803 0.28411115
@holidayworking () R 16 2006 6 26 8 / 18

9. > <- factanal( , factors=2)
> print( , cutoff=0)
Call:
factanal(x = , factors = 2)
Uniquenesses
Loadings
Uniquenesses:
SS loadings
0.471 0.395 0.379 0.548 0.491 Proportion Var
Loadings: Cumulative Var
Factor1 Factor2
0.722 0.084
0.730 0.268
0.177 0.768
0.156 0.654
0.537 0.470
Factor1 Factor2
SS loadings 1.399 1.317
Proportion Var 0.280 0.263
Cumulative Var 0.280 0.543
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.08 on 1 degree of freedom.
@holidayworking ()
The p-value is 0.782 R 16 2006 6 26 9 / 18

10. 1
> <- 1 - $uniquenesses
>
0.5288198 0.6049597 0.6213085 0.4523362 0.5087881
@holidayworking () R 16 2006 6 26 10 / 18

11. 1 2
0.722 0.084 0.529
0.730 0.268 0.605
0.537 0.470 0.509
0.177 0.768 0.621
0.156 0.654 0.452
0.722 1.317
1
⇒
2
⇒
@holidayworking () R 16 2006 6 26 11 / 18

12. @holidayworking () R 16 2006 6 26 12 / 18

13. > <- factanal( , factors=2,rotation="promax")
> print( , cutoff=0)
Call:
factanal(x = , factors = 2, rotation = "promax")
Uniquenesses:
0.471 0.395 0.379 0.548 0.491
Loadings:
Factor1 Factor2
0.801 -0.156
0.749 0.050
-0.051 0.815
-0.038 0.692
0.461 0.348
Factor1 Factor2
SS loadings 1.419 1.291
Proportion Var 0.284 0.258
Cumulative Var 0.284 0.542
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.08 on 1 degree of freedom.
@holidayworking ()
The p-value is 0.782 R 16 2006 6 26 13 / 18

14. > <- factanal( , factors=2,rotation="none")
> print( , cutoff=0)
Call:
factanal(x = , factors = 2, rotation = "none")
Uniquenesses:
0.471 0.395 0.379 0.548 0.491
Loadings:
Factor1 Factor2
0.583 -0.435
0.714 -0.307
0.657 0.436
0.563 0.368
0.713 -0.028
Factor1 Factor2
SS loadings 2.106 0.611
Proportion Var 0.421 0.122
Cumulative Var 0.421 0.543
Test of the hypothesis that 2 factors are sufficient.
The chi square statistic is 0.08 on 1 degree of freedom.
@holidayworking ()
The p-value is 0.782 R 16 2006 6 26 14 / 18

15. > <- promax(loadings( ), m=4)
> print( )
$loadings
Loadings:
Factor1 Factor2
0.801 -0.156
0.749
0.815
0.692
0.461 0.348
Factor1 Factor2
SS loadings 1.419 1.291
Proportion Var 0.284 0.258
Cumulative Var 0.284 0.542
$rotmat
[,1] [,2]
[1,] 0.6062459 0.5303245
[2,] -1.0284319 1.0695617
@holidayworking () R 16 2006 6 26 15 / 18

16. rotmat
> <- solve(t( $rotmat)%*%
$rotmat)
>
[,1] [,2]
[1,] 1.0000000 0.5462117
[2,] 0.5462117 1.0000000
1 2 0.5462117
@holidayworking () R 16 2006 6 26 16 / 18

17. R factanal
@holidayworking () R 16 2006 6 26 17 / 18

18. @holidayworking () R 16 2006 6 26 18 / 18