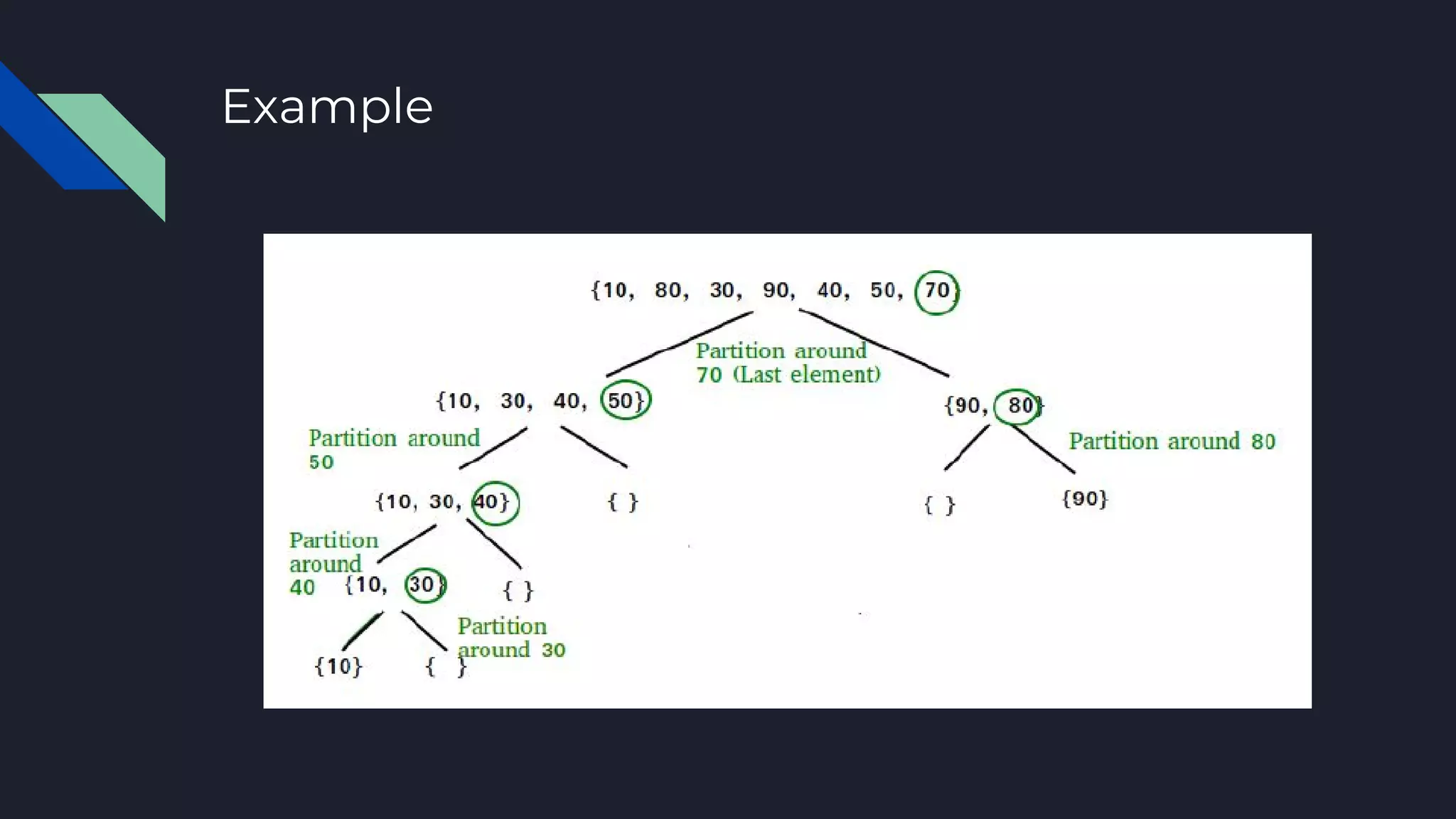
Quicksort is a divide and conquer algorithm that works by picking an element as a pivot and partitioning the array around it. It recursively sorts elements before and after the pivot. The average runtime is O(n log n) but it can be O(n^2) in the worst case if the pivot selection is poor. The algorithm involves picking a pivot element, partitioning the array around it, and then recursively sorting the subarrays.

1. Algorithms
Quick Sort
Abdelrahman M. Saleh

2. List of contents
● Introduction
● Example w/ illustrating figures
● Algorithm
● implementation (Java, C++, Python)
● Performance Runtime
○ Best, Average and worst cases.
● Execution
● Other Notes

3. Introduction
● Like Merge sort it’s Divide and Conquer algorithm => picks an element as pivot and
partitions the given array around it
● There are many different versions of quickSort that pick pivot in different ways
○ Always pick first element as pivot.
○ Always pick last element as pivot (implemented below)
○ Pick a random element as pivot.
○ Pick median as pivot.

4. Example

5. Algorithm .
➔ Array name “arr” , starting index “low”, ending index “high”
● If low is smaller than high
○ pivot is partitioning index, arr[p] is now at right place :
■ pivot = partition(arr, low, high)
○ Recursively sort elements Aefore pivot :
■ Call quickSort(arr, low, pivot - 1)
○ Recursively sort elements After pivot :
■ Call quickSort(arr, pivot + 1, high)

6. Implementation .

7. C++
void quickSort(int arr[], int low, int high)
{
if (low < high)
{
int pivot = partition(arr, low, high);
quickSort(arr, low, pivot - 1);
quickSort(arr, pivot + 1, high);
}
}

8. C++
Continue ...
int partition (int arr[], int low, int high)
{
int pivot = arr[high], i = (low - 1);
for (int j = low; j <= high- 1; j++)
{
if (arr[j] <= pivot)
{
I++; swap(&arr[i], &arr[j]);
}
}
swap(&arr[i + 1], &arr[high]);
return (i + 1);
}
// partition the array around the pivot

9. JAVA
void sort(int arr[], int low, int high)
{
if (low < high)
{
int pi = partition(arr, low, high);
sort(arr, low, pi-1);
sort(arr, pi+1, high);
}
}

10. JAVA
Continue ...
int partition(int arr[], int low, int high) {
int pivot = arr[high], i = (low-1);
for (int j=low; j<high; j++)
{
if (arr[j] <= pivot)
{
i++;
int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; //swap of [i] & [j]
}
}
int temp = arr[i+1]; arr[i+1] = arr[high]; arr[high] = temp; //swap of [i+1] & [high]
return i+1;
}
// partition the array around the pivot

11. Python .
def quickSort(arr,low,high):
if low < high:
pi = partition(arr,low,high)
quickSort(arr, low, pi-1)
quickSort(arr, pi+1, high)

12. Python
Continue ...
def partition(arr,low,high):
i = ( low-1 )
pivot = arr[high]
for j in range(low , high):
if arr[j] <= pivot:
i = i+1
arr[i],arr[j] = arr[j],arr[i]
arr[i+1],arr[high] = arr[high],arr[i+1]
return ( i+1 )
// partition the array around the pivot

13. Performance Runtime
● Time complexity F(n) = F(k) + F(n-k-1) +Θ(n) .
● Best case : always picks the middle element as pivot :
○ F(n) = 2F(n/2) + Θ(n) => Θ(nlogn) .
● Worst case : always picks greatest or smallest element as pivot :
○ F(n) = F(0) + F(n-1) +Θ(n) => Θ(n2
) .
● Average case : could be considered when partition puts O(n/9) elements in one set and
O(9n/10) elements in other set :
○ F(n) = F(n/9) + F(9n/10) + Θ(n) .

14. Execution .
Input array : [4, 6, 3, 2, 1, 9, 7]
Swap Pivot “7” with “9”
=> left part [4, 6, 3, 2, 1] right part[9]
Swap Pivot “1”, 4
Swap 6, 2
=> left part [3, 2] right [4, 6]
Swap Pivot “2”, 3
=> left part [3] right [4, 6]
Output Array: [1, 2, 3, 4, 6, 7, 9]

15. Other Notes .
● Algorithmic Paradigm: Divide Approach
● Sorting In Place: Yes
● Stable: Yes
● Online: Yes