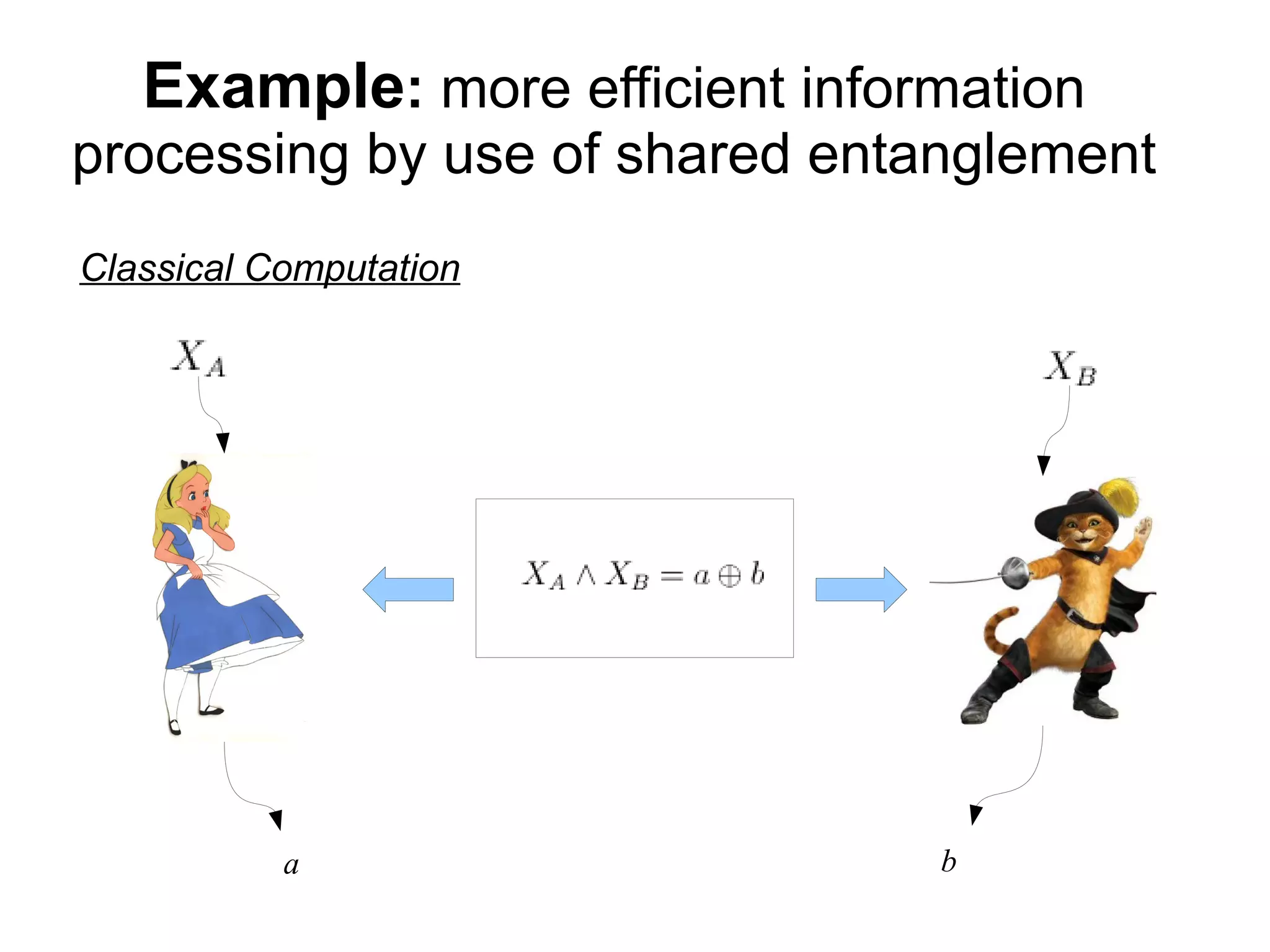
1) The document discusses quantum computation, including basic concepts like qubits, superposition, entanglement, and EPR paradox. 2) It explains that quantum computers can perform operations on data using quantum phenomena like superposition and entanglement. This allows for computations that classical computers cannot perform under the Church-Turing thesis. 3) Examples are given showing how a quantum protocol using an entangled EPR pair can solve a certain information processing task more efficiently than a classical protocol.

1. Teachers
Bruno Benedetti
Lorenzo Orecchia
Student
Stefano FrancoBari, 26/07/2013

2. “God does not throw dice”
(Einstein, 4 December 1926)

3. Summary
● Introduction
● Basic Quantum Mechanics
● Qubit
● EPR Paradox
● Bell's inequality
● Example
● References
● Conclusions

4. Introduction
A quantum computer is a computation device that makes direct use
of quantum-mechanical phenomena, such as superposition and
entanglement, to perform operations on data.
Why Quantum Computation?
● No limitations on computation imposed by the extended Church-
Tuing thesis
● Random number
● No cloning
● Quantum teleportation
● Non-locality (entanglement)
● Cryptography
What is Quantum Computation?

5. Basic Quantum Mechanics
(postulates)
1. Superposition Principle
2. Measurement Principle
3. Unitary evolution

6. Qubits (or quantum bit)
The basic entity of quantum information (analogue of the bit for
classical computation)
Sfera di Bloch
Curiosity: how many information can be
stored by a qubit?
Exactly 2, like a classical bit
(Holevo, 1973)

7. Two Qubits
0 0
1 1
Can we say what the state of each of
the individual qubits is? NO: entanglement!
Bell's states (or EPR pairs)
maximally entangled states of two
qubits

8. EPR Paradox (1935)
Can quantum mechanics
be complete?
Einstein Podolsky Rosen
Assumption
1. Physics reality
2. Locality
3. Completeness
Bell's state
There exist local hidden variables!

9. Bell's Inequality (1964)
(experimentally Aspect and co-workers, 1981)
“There does not exist any local
hidden variable theory consistent
with outcomes of quantum physics”
Consequences
● Entanglement is not paradossal
● Quantum correlations in an EPR pair are
“stronger” than classical correlations

10. Example: more efficient information
processing by use of shared entanglement
Classical Computation
a b

11. YOU WIN 75% OF THE TIMES

12. Quantum Computation
Protocol:
EPR pair
CLAIM:

13. Recall (superpositional principle and rotation matrix)
In general, rotation of a state
by an angle in the two-dimensional state space gives the rotaded state
where
Hence the probability of measuring a 0 for the rotated state is given by

14. By calculating:
Let's start:

15. Conclusion:
With Quantum Computer you can win more often!
YOU WIN 85% OF THE TIMES

16. References
● Wikipedia
- Paradosso EPR
- Teoria delle variabili nascoste
- Teorema di Bell
- Qubit
- Entanglement quantistico
- Notazione bra-ket
- Informatica quantistica
- Ampiezza di probabilità
● Introduction, Axioms, Bell Inequalities (Lecture 1, Spring 2007,
CS 294-2)
● Qubit gates and EPR (Lecture 5, Fall 2007, C/CS/Phys C191)
● Entanglement can facilitate information processing (Lecture 5,
Fall 2005, C/CS/Phys C191)

17. Conclusions
About the course
Very interesting course, in many respects. These
activities improve people and institutions. I hope it will
be the first of many others.
About Quantum Computation
I think that the current paradoxes about quantum
mechanics are comparable to Zenone's paradoxes.
One day, perhaps, all things will be clearer.

18. “God does not throw dice”
But we really love doing it!

19. – The end –