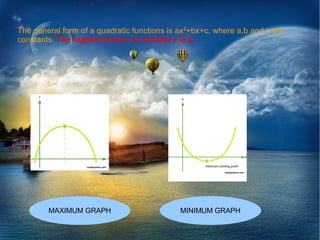
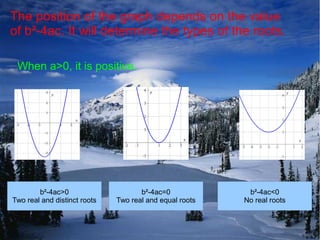
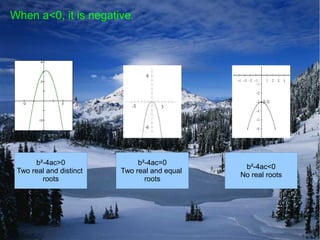
1. The quadratic function f(x) = ax^2 + bx + c has a maximum value if a < 0 and a minimum value if a > 0. 2. The maximum and minimum values can be determined by completing the square, writing the function as a(x + p)^2 + q. 3. Quadratic inequalities can be solved by graphing, with the negative region shaded if the inequality sign is < 0. Factorization using a calculator can also solve inequalities.

2. The general form of a quadratic functions is ax²+bx+c, where a,b and c are
constants. The highest power of variable x is 2.
MAXIMUM GRAPH MINIMUM GRAPH

3. The position of the graph depends on the value
of b²-4ac. It will determine the types of the roots.
When a>0, it is positive.
b²-4ac>0 b²-4ac=0 b²-4ac<0
Two real and distinct roots Two real and equal roots No real roots

4. When a<0, it is negative.
b²-4ac>0 b²-4ac=0
b²-4ac<0
Two real and distinct Two real and equal
No real roots
roots roots

5. EXAMPLE:
Find the values of p if the graph of quadratic function
f(x)= (2-3p)x² + (4-p)x+2 touches the x axis at only one point.
So, a=2-3p
First you should divide the values of
b= 4-p
a, b and c from this equation
c=2
Since it touches at only one point, so
b²-4ac=0 will be applied.
(4-p)²-4(2-3p)(2)=0
p²-8p+16-16+24p=0
p²+16p=0
p(p+16)=0
p=0 or p= -16

6. Example:
Find the range of values of m if the graph of quadratic functions
h(x)= x² – 2(4m+1)x + 16m²-3 cuts the x axis at two distinct
points.
So, a= 1
First you should divide the values of
b= -2(4m+1)
a, b and c from this equation
c= 16m²-3
Since, it cuts the x axis at two distinct points,
so b²-4ac >0 will be applied.
[-2(4m+1)]²-4(1)(16m²-3) > 0
4(16m²+8m+1) – 64m²+12 > 0
64m² + 32m + 4- 64m²+12 > 0
32m + 16 > 0
32m > -16
m > -16
32
m > -1
2

7. 1. The quadratic function f(x) = ax² + bx + c
has a maximum value if the coefficient of
x² is negative ( a<0) and a minimum value
if the coefficient of x² is positive ( a>0)
2. The maximum and minimum value of a
quadratic function f(x) = ax² + bx + c can
be determined by completing the square
by expressing ax² + bx + c in the form of
a(x+p)²+q.

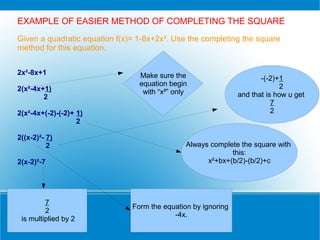
8. Example:
Express the following quadratic equation in the form of a(x+p)² + q. State the
maximum / minimum value of the the function and corresponding value of x.
f(x)= 2x² + 7x + 10
2x² + 7x + 10
2(x² + 7x + 10)
2( x² + 7 x + 5)
Normal completing
2
square method
2[x² + 7/2 x + (7/4)²- (7/4)² + 5]
2(x + 7/4)² + 31/16
2(x+7/4)² + 31/8

9. EXAMPLE OF EASIER METHOD OF COMPLETING THE SQUARE
Given a quadratic equation f(x)= 1-8x+2x². Use the completing the square
method for this equation.
2x²-8x+1 Make sure the -(-2)+1
equation begin 2
2(x²-4x+1) with “x²” only
2 and that is how u get
7
2(x²-4x+(-2)-(-2)+ 1) 2
2
2((x-2)²- 7)
2 Always complete the square with
this:
2(x-2)²-7 x²+bx+(b/2)-(b/2)+c
7
Form the equation by ignoring
2
-4x.
is multiplied by 2

10. Quadratic inequalities can be solved by graph sketching method.
Example:
x² – 11x + 24 < 0 Since the “ x² ” is in positive, it
will be minimum graph Positive
Since “<0” it is negative
Factorisation method should
be used. It can be used using
calculator.
Press “MODE” (3 times),
Press “1” for “EQN”,
Negative should Press the arrow button for
be shaded right (degree) and press “2”
So, a= 1
b= -11
c= 24
Negative You will get values of x as 8
and 3.