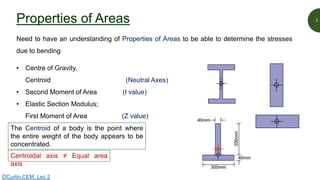
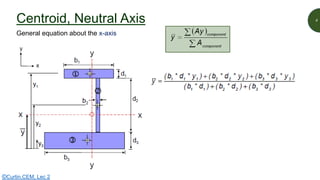
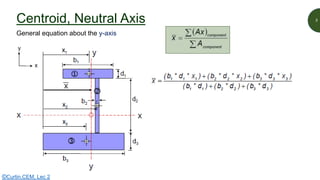
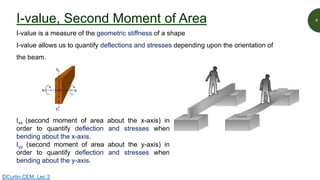
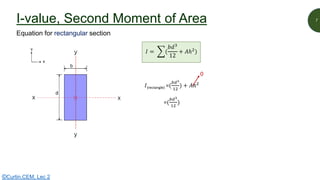
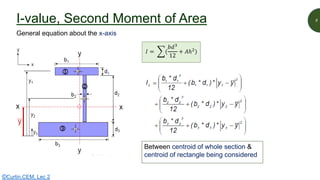
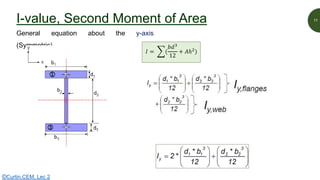
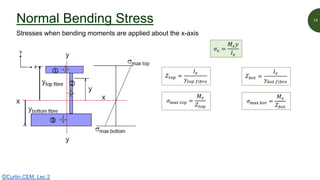
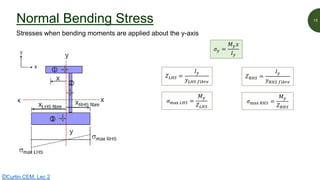
This document discusses key properties of areas that are important for determining stresses in structural elements. It defines centroid (also called neutral axis) as the point where the entire weight of a body appears concentrated. The second moment of area (I-value) is introduced as a measure of geometric stiffness that allows quantification of deflections and stresses depending on beam orientation. Elastic section modulus (Z-value) is equal to the second moment of area divided by the distance to the extreme fiber, and is used together with the bending moment to determine maximum normal stresses in a beam. Formulas are provided for calculating these properties for basic shapes like rectangles.

1. KSI ENGINEERING
PROPERTIES
OF AREAS
Toe Myint Naing
Curtin Malaysia
Intern

2. 2Normal Stress Distribution
• When external axial loads are applied,
they are resisted by internal normal
stresses acting over the cross sectional
area of the section.
• When external bending moments are
applied, they need to be resisted by an
internal resisting couple. It therefore
follows that we need a first moment of area
to help determine the stresses in a beam
subjected to a moment.
(lbf/𝑖𝑛2)
(lbf/𝑖𝑛2)
©Curtin,CEM, Lec 2

3. 3Properties of Areas
Need to have an understanding of Properties of Areas to be able to determine the stresses
due to bending
• Centre of Gravity,
Centroid (Neutral Axes)
• Second Moment of Area (I value)
• Elastic Section Modulus;
First Moment of Area (Z value)
The Centroid of a body is the point where
the entire weight of the body appears to be
concentrated.
Centroidal axis ≠ Equal area
axis
©Curtin,CEM, Lec 2

4. Centroid, Neutral Axis
General equation about the x-axis
4
©Curtin,CEM, Lec 2

5. Centroid, Neutral Axis
General equation about the y-axis
5
©Curtin,CEM, Lec 2

6. I-value, Second Moment of Area
I-value is a measure of the geometric stiffness of a shape
I-value allows us to quantify deflections and stresses depending upon the orientation of
the beam.
6
©Curtin,CEM, Lec 2
Ixx (second moment of area about the x-axis) in
order to quantify deflection and stresses when
bending about the x-axis.
Iyy (second moment of area about the y-axis) in
order to quantify deflection and stresses when
bending about the y-axis.

7. I-value, Second Moment of Area 7
©Curtin,CEM, Lec 2
𝐼(rectangle) =(
𝑏𝑑3
12
) + 𝐴ℎ2
=(
𝑏𝑑3
12
)
0
Equation for rectangular section
𝐼 = (
𝑏𝑑3
12
+ 𝐴ℎ2
)

8. I-value, Second Moment of Area 8
©Curtin,CEM, Lec 2
𝐼 = (
𝑏𝑑3
12
+ 𝐴ℎ2
)
General equation about the x-axis
Between centroid of whole section &
centroid of rectangle being considered

9. I-value, Second Moment of Area 9
©Curtin,CEM, Lec 2
General equation about the y-axis
Between centroid of whole section &
centroid of rectangle being considered
𝐼 = (
𝑏𝑑3
12
+ 𝐴ℎ2
)

10. I-value, Second Moment of Area 10
©Curtin,CEM, Lec 2
General equation about the x-axis
(Symmetric)
𝐼 = (
𝑏𝑑3
12
+ 𝐴ℎ2
)

11. I-value, Second Moment of Area 11
©Curtin,CEM, Lec 2
General equation about the y-axis
(Symmetric)
𝐼 = (
𝑏𝑑3
12
+ 𝐴ℎ2
)

12. First Moment of Area, Elastic Section Modulus (Z) 12
©Curtin,CEM, Lec 2
Equation for rectangular section
𝑍 𝑥 =
𝐼 𝑥
𝑦 𝑚𝑎𝑥

13. Normal Bending Stress 13
©Curtin,CEM, Lec 2
𝜎 𝑚𝑎𝑥 =
𝑀𝑦 𝑚𝑎𝑥
𝐼
𝑍 =
𝐼
𝑦 𝑚𝑎𝑥
∴ 𝜎 𝑚𝑎𝑥 =
𝑀
𝑍
∴ Stresses are related to the Z value
1
𝑅
=
𝑀
𝐸𝐼
∴ ∆=
𝑀
𝐸𝐼
(constant)
∴ Deflections are related to the I value
(and E)

14. Normal Bending Stress
Stresses when bending moments are applied about the x-axis
𝜎 𝑥 =
𝑀 𝑥 𝑦
𝐼 𝑥
𝑍𝑡𝑜𝑝 =
𝐼 𝑥
𝑦𝑡𝑜𝑝 𝑓𝑖𝑏𝑟𝑒
𝜎max 𝑡𝑜𝑝 =
𝑀 𝑥
𝑍𝑡𝑜𝑝
𝑍 𝑏𝑜𝑡 =
𝐼 𝑥
𝑦 𝑏𝑜𝑡 𝑓𝑖𝑏𝑟𝑒
𝜎max 𝑏𝑜𝑡 =
𝑀 𝑥
𝑍 𝑏𝑜𝑡
©Curtin,CEM, Lec 2
14

15. Normal Bending Stress
Stresses when bending moments are applied about the y-axis
𝜎 𝑦 =
𝑀 𝑦 𝑥
𝐼 𝑦
𝑍 𝐿𝐻𝑆 =
𝐼 𝑦
𝑦 𝐿𝐻𝑆 𝑓𝑖𝑏𝑟𝑒
𝜎max 𝐿𝐻𝑆 =
𝑀 𝑦
𝑍 𝐿𝐻𝑆
𝑍 𝑅𝐻𝑆 =
𝐼 𝑦
𝑦 𝑅𝐻𝑆 𝑓𝑖𝑏𝑟𝑒
𝜎max 𝑅𝐻𝑆 =
𝑀 𝑦
𝑍 𝑅𝐻𝑆
©Curtin,CEM, Lec 2
15

16. Thank
sFor your attention

17. Any
Question?