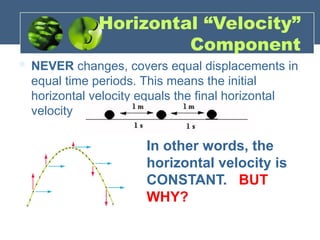
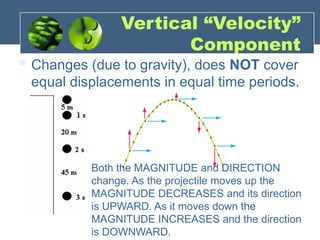
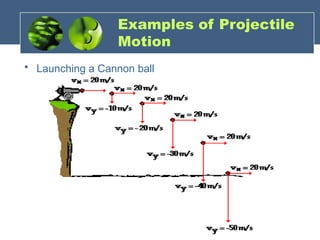
Projectile motion refers to the trajectory of an object influenced only by gravity, characterized by horizontal and vertical components. It can exhibit various types such as horizontal, vertical, and parabolic motion, with key features like constant horizontal velocity and changing vertical velocity due to gravity. The document also explains concepts such as impulse and momentum, providing equations and sample problems for better understanding.

1. What is Projectile
Motion?

2. Projectile
• A projectile is an object upon
which the only force acting is
gravity.
• Any object that is given an initial
velocity and then follows a path
determined entirely by
gravitational acceleration.

3. Projectile Motion
• Projectile is a combination of
uniform horizontal motion and free
fall motion.
• Trajectory- curved path of a
projectile
• Range (R)- horizontal
displacement, dependent on the
angle of projection

4. Projectile Motion
• Projectile motion is a predictable path
traveled by an object that is influenced only
by the initial launch speed, launch angle,
and the acceleration due to gravity.
• Two-dimensional motion of an object
– Vertical
– Horizontal

5. Projectile Motion
• Italian Scientist Galileo Galilei first
describe projectile motion as having
two components: horizontal and
vertical.

6. Types of Projectile
Motion
• Horizontal
– Motion of a ball rolling freely
along a level surface
– Horizontal velocity is ALWAYS
constant
• Vertical
– Motion of a freely falling object
– Force due to gravity
– Vertical component of velocity
changes with time
• Parabolic
– Path traced by an object
accelerating only in the vertical
direction while moving at
constant horizontal velocity

7. Types of Projectile
Motion
• If air resistance is neglected, a projectile
moves horizontally at a constant speed
and simultaneously travels vertically with
an acceleration equal to g, which is 9.8
m/s²
• Note: the motion of freely falling
body is a special case of projectile
motion where the horizontal velocity
is 0.

8. Horizontal “Velocity”
Component
 NEVER changes, covers equal displacements in
equal time periods. This means the initial
horizontal velocity equals the final horizontal
velocity
In other words, the
horizontal velocity is
CONSTANT. BUT
WHY?

9. Vertical “Velocity”
Component
 Changes (due to gravity), does NOT cover
equal displacements in equal time periods.
Both the MAGNITUDE and DIRECTION
change. As the projectile moves up the
MAGNITUDE DECREASES and its direction
is UPWARD. As it moves down the
MAGNITUDE INCREASES and the direction
is DOWNWARD.

10. Projectile Launched
at an Angle
 If a projectile is launched at an angle either
below or above the horizontal, you need to
resolve the initial velocity into its horizontal
and vertical components.
 Range- launching point which measured on
the assumption that the projectile returns to
the same level from which it is fired.
 Time symmetry- the for the projectile to
reach the maximum height equals the time
for it to land

11. Projectile Launched
at an Angle
 Speed Symmetry- shows that the speed of
the projectile at any height above the
starting point on its way up is equal to its
speed at the same height on the way down.
 Absolute values o the angles that these
speeds make with the horizontal are also
are also equal.
 The velocities are not equal because they
point in opposite directions.

12. Examples of Projectile
Motion
• Launching a Cannon ball

14. Kinematics of
Projectile Motion
1. VO – initial velocity
2. Vox and Voy- initial horizontal and initial
vertical velocities.
3. Vx and Vy- instantaneous horizontal
and instantaneous vertical velocities
4. Ѳ – is the angle of projection.

15. X-COMPONENT Y-COMPONENT
VECTORS
X-DIRECTION Y-DIRECTION
V
dy= Voyt+ gt
gd

16. Impulse and Momentum
Impulse produced by a force
changes momentum.
Linear momentum or momentum
is the product of the mass of the
object and its velocity. P is a symbol
for momentum.

17. Impulse and Momentum
It is a vector quantity and an SI
unit of kg•m/s.
p=mv
Every moving object has
momentum, which may be large
or small depending on the
object’s mass and velocity.

18. Sample Problem
Which has a greater
momentum: a cheetah with a mass
of about 74kg and a running speed
of up to 31m/s, or an elephant with
a mass of 7000kg running at
18km/hr?

19. Sample Problem
A delivery truck carrying 75 cavans of rice is
traveling at 10.0 m/s. The mass of the truck and
one cavan of rice are 3000kg and 50kg,
respectively. The driver of the truck has a mass of
85kg.
(a) What is the momentum of the truck with the
driver and the cavans of rice?
(b) At a certain grocery, the driver unloaded 8
cavans. What is the new momentum of the
truck with the driver and the cavans of rice if
the driver maintains the same speed?

20. Impulse-Momentum
Theorem
Impulse- the product of force and
the time it acts on an object.
Impulse is represented by a capital
letter I.
I = Ft
Note: Newton’s Law of Acceleration

21. Impulse-Momentum
Theorem
 Impulse produced by a force changes
momentum. It is a vector quantity and SI
unit is N*s.
 A force acting on an object for a time
interval ∆t changes the momentum of the
object.
 Change in momentum of a system is equal
to the impulse of the force it experience.
Note: Newton’s Law of Acceleration

22. Impulse-Momentum
Theorem
F∆t= mv-mv0
Note that ∆t= t-t0 Setting t0 = 0, you
have
Ft=mv-mv0

23. Sample Problem
1. A force of 56.0 N acts on 25.0 kg for
12.0 s. Find the (a) impulse produced
by the force (b) resulting change in
momentum of the body, and (c)
speed of the body at the end of 12.0
s. Assume that the body starts from
rest.

24. Sample Problem
Given:
m = 25kg F = 56N
t = 12s v0= 0

25. Solution:
(a)I = Ft = (56N)(12s) =672N.s
(b)The impulse produced by the force is
equal to the change in momentum of the
body. Therefore, the change in
momentum is 672 kg-m/s.
(c) Using the impulse-momentum theorem,
you can get
(d)Ft = mv – mv0
672Ns = (25kg) * v + 0
v = 26.9m / s