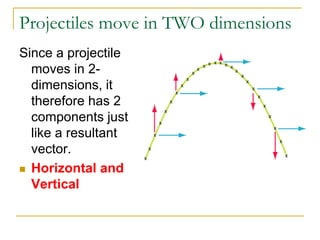
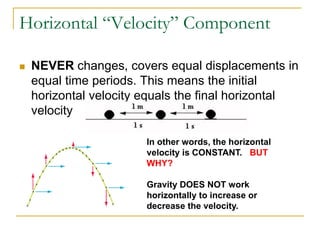
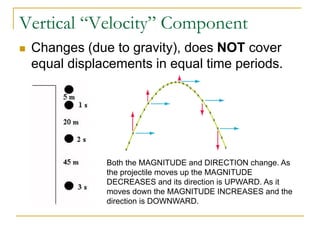
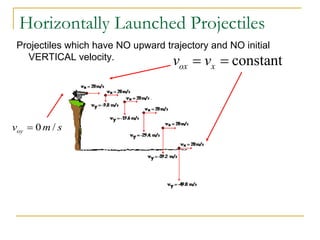
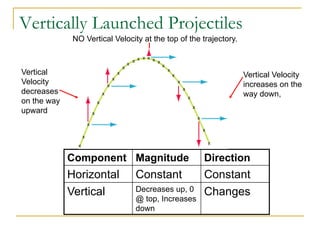
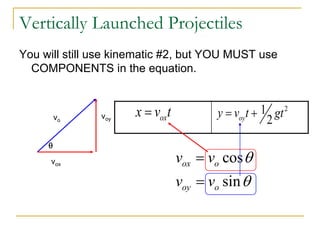
Projectile motion refers to the movement of an object in the x-y plane, influenced primarily by gravity, resulting in a parabolic trajectory. Key components of projectile motion include constant horizontal velocity and changing vertical velocity due to gravitational acceleration. Examples of projectiles include baseballs, bullets, and the space shuttle post-engine cut-off, and calculations are often performed using kinematic equations for both horizontal and vertical motions.

1. Projectile Motion

2. What is projectile?
◼ Projectile is any object which projected by some means
and continues to move due to its own inertia (mass).
◼ The path of a projectile is called its trajectory.
◼ The force of primary importance acting on a projectile is
gravity
◼ A projectile is any object with an initial non-zero.
Horizontal velocity whose acceleration is due to gravity
alone
◼ The kinematic equations for a simple projectile are those
of an object traveling at constant horizontal velocity and
constant vertical acceleration.
◼ The trajectory of a simple projectile is a parabola

3. What is projectile?
◼ Projectile motion can be
described as the motion of an
object (called the projectile) that is
moving in the x-y plane. This just
means that the motion of the
projectile is the vector sum of its
horizontal and vertical motion.

4. Examples of projectile?
◼ A baseball that has been pitched, batted, or thrown
◼ A bullet the instant in exits the barrel of a gun or rifle
◼ A bus drove off an uncompleted bridge
◼ A moving airplane in the air with its engines and
wings disabled
◼ A runner in mid-stride (since they momentarily lose
contact with the ground)
◼ The space shuttle or any other spacecraft after the
main engine cut-ff

5. Projectiles move in TWO dimensions
Since a projectile
moves in 2-
dimensions, it
therefore has 2
components just
like a resultant
vector.
◼ Horizontal and
Vertical

6. Horizontal “Velocity” Component
◼ NEVER changes, covers equal displacements in
equal time periods. This means the initial
horizontal velocity equals the final horizontal
velocity
In other words, the horizontal
velocity is CONSTANT. BUT
WHY?
Gravity DOES NOT work
horizontally to increase or
decrease the velocity.

7. Vertical “Velocity” Component
◼ Changes (due to gravity), does NOT cover
equal displacements in equal time periods.
Both the MAGNITUDE and DIRECTION change. As
the projectile moves up the MAGNITUDE
DECREASES and its direction is UPWARD. As it
moves down the MAGNITUDE INCREASES and the
direction is DOWNWARD.

8. Combining the Components
Together, these
components produce
what is called a
trajectory or path. This
path is parabolic in
nature.
Component Magnitude Direction
Horizontal Constant Constant
Vertical Changes Changes

9. Combining the Components
◼ Along the horizontal, the velocity is
constant and free from acceleration (a =
0). The acceleration is only present in the
vertical. The kinematic equations still apply
in projectile motion. A point to consider in
projectile motion is that at its maximum
height, the vertical component of the
velocity becomes zero.

10. Kinematic Equation for Projectile Motion
Horizontal Motion Vertical Motion
ax = 0 vx – constant ay = -ag = constant
vfx = vix vfy = viy - agt
xf = xi + vixt yf = yi + viyt – ½ ag
vfy
2 = viy
2 – 2ag (yf – yi)

11. Horizontally Launched Projectiles
Projectiles which have NO upward trajectory and NO initial
VERTICAL velocity.
0 /
oy
v m s
=
constant
ox x
v v
= =

12. Horizontally Launched Projectiles
To analyze a projectile in 2 dimensions we need 2
equations. One for the “x” direction and one for
the “y” direction. And for this we use kinematic #2.
2
1
2
ox
x v t at
= +
ox
x v t
=
Remember, the velocity is
CONSTANT horizontally, so
that means the acceleration
is ZERO!
2
1
2
y gt
=
Remember that since the
projectile is launched
horizontally, the INITIAL
VERTICAL VELOCITY is
equal to ZERO.

13. Horizontally Launched Projectiles
Example: A plane traveling with
a horizontal velocity of 100
m/s is 500 m above the
ground. At some point the
pilot drops a bomb on a
target below. (a) How long is
the bomb in the air? (b) How
far away from point above
where it was dropped will it
land?
What do I
know?
What I want to
know?
vox=100 m/s t = ?
y = 500 m x = ?
voy= 0 m/s
g = 9.8 m/s/s

14. Horizontally Launched Projectiles
2 2
2
1 1
500 ( 9.8)
2 2
102.04
y gt t
t t
= → − = −
= → = 10.1 seconds
(100)(10.1)
ox
x v t
= = = 1010 m

15. Seatwork
◼ A cannon ball is fired with a horizontal
velocity of 300 m/s from the top of a cliff 60 m
high. How far from the base of cliff will it hit
the ground?

16. Example 1
◼ A baseball is thrown upward with a speed of 20 m/s
at an angle of 40o from the horizontal. Determine
the horizontal and vertical components of its
velocity.
Solution:
◼ From our review of trigonometry and vector
resolution, we know that the horizontal component
of the vector is given by the cosine function and the
vertical component by the sine function. Hence,
vx =vcosθ
vy =vsinθ

17. Example 1
◼ From the problem, the following data were
gleaned:
v=20ms θ = 40°
◼ Therefore, the horizontal and vertical
components of the baseball’s velocity are
vx =vcosθ =(20m/s)cos(40°)
vx =15.321m/s
vy =vsinθ =(20ms)sin(40°)
vy =12.856m/s

18. Vertically Launched Projectiles
Horizontal Velocity
is constant
Vertical
Velocity
decreases
on the way
upward
Vertical Velocity
increases on the
way down,
NO Vertical Velocity at the top of the trajectory.
Component Magnitude Direction
Horizontal Constant Constant
Vertical Decreases up, 0
@ top, Increases
down
Changes

19. Vertically Launched Projectiles
Since the projectile was launched at an angle, the
velocity MUST be broken into components!!!
vo
vox
voy
q
cos
sin
ox o
oy o
v v
v v
q
q
=
=

20. Vertically Launched Projectiles
There are several
things you must
consider when doing
these types of
projectiles besides
using components. If
it begins and ends at
ground level, the “y”
displacement is
ZERO: y = 0

21. Vertically Launched Projectiles
You will still use kinematic #2, but YOU MUST use
COMPONENTS in the equation.
vo
vox
voy
q
ox
x v t
= 2
1
2
oy
y v t gt
= +
cos
sin
ox o
oy o
v v
v v
q
q
=
=

22. Example
A place kicker kicks a football with a velocity of 20.0 m/s
and at an angle of 53 degrees.
(a) How long is the ball in the air?
(b) How far away does it land?
(c) How high does it travel?
q = 53
cos
20cos53 12.04 /
sin
20sin53 15.97 /
ox o
ox
oy o
oy
v v
v m s
v v
v m s
q
q
=
= =
=
= =

23. Example
A place kicker kicks a
football with a
velocity of 20.0 m/s
and at an angle of 53
degrees.
(a) How long is the ball
in the air?
What I know What I want
to know
vox=12.04 m/s t = ?
voy=15.97 m/s x = ?
y = 0 ymax=?
g = - 9.8
m/s/s
2 2
2
1 0 (15.97) 4.9
2
15.97 4.9 15.97 4.9
oy
y v t gt t t
t t t
t
= + → = −
− = − → =
= 3.26 s

24. Example
A place kicker kicks a
football with a
velocity of 20.0 m/s
and at an angle of 53
degrees.
(b) How far away does it
land?
What I know What I want
to know
vox=12.04 m/s t = 3.26 s
voy=15.97 m/s x = ?
y = 0 ymax=?
g = - 9.8
m/s/s
(12.04)(3.26)
ox
x v t
= → = 39.24 m

25. Example
A place kicker kicks a
football with a velocity
of 20.0 m/s and at an
angle of 53 degrees.
(c) How high does it
travel?
CUT YOUR TIME IN HALF!
What I know What I want
to know
vox=12.04 m/s t = 3.26 s
voy=15.97 m/s x = 39.24 m
y = 0 ymax=?
g = - 9.8
m/s/s
2
2
1
2
(15.97)(1.63) 4.9(1.63)
oy
y v t gt
y
y
= +
= −
= 13.01 m