Lec5_Product & Quotient Rule.ppt

The Product and Quotient RULES

The Product and
Quotient Rules
DIFFERENTIATION RULES
In this section, we will learn about:
Formulas that enable us to differentiate new functions
formed from old functions by multiplication or division.

By analogy with the Sum and Difference
Rules, one might be tempted to guess—as
Leibniz did three centuries ago—that the
derivative of a product is the product of the
derivatives.
 However, we can see that this guess is wrong
by looking at a particular example.
THE PRODUCT RULE

Let f(x) = x and g(x) = x2.
 Then, the Power Rule gives f’(x) = 1 and g’(x) = 2x.
 However, (fg)(x) = x3.
 So, (fg)’(x) =3 x2.
 Thus, (fg)’ ≠ f’ g’.
THE PRODUCT RULE

The correct formula was discovered by
Leibniz (soon after his false start) and is
called the Product Rule.
THE PRODUCT RULE

Before stating the Product Rule, let’s see
how we might discover it.
We start by assuming that u = f(x) and
v = g(x) are both positive differentiable
functions.
THE PRODUCT RULE

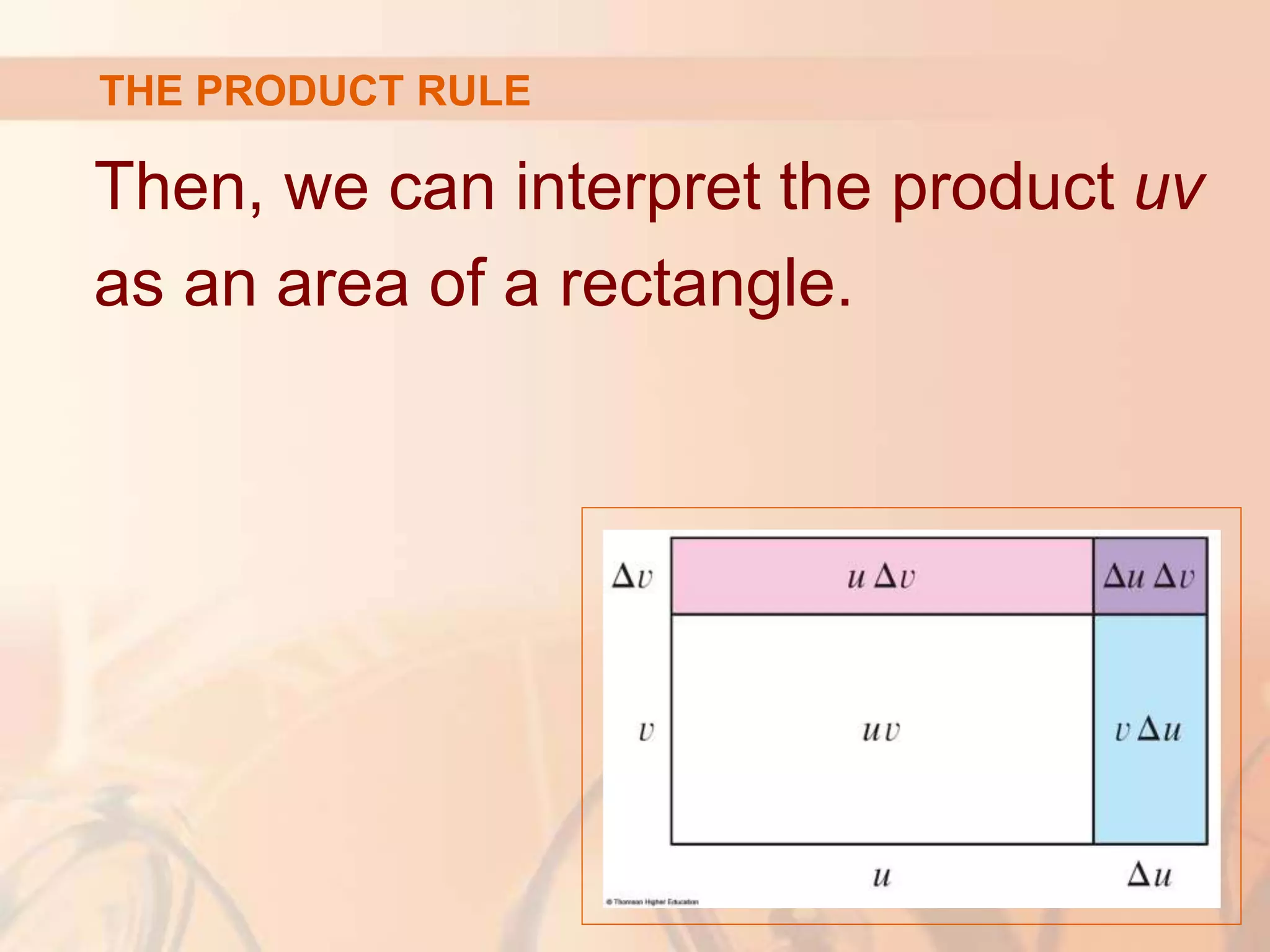
Then, we can interpret the product uv
as an area of a rectangle.
THE PRODUCT RULE

If x changes by an amount Δx, then
the corresponding changes in u and v
are:
 Δu = f(x + Δx) - f(x)
 Δv = g(x + Δx) - g(x)
THE PRODUCT RULE

The new value of the product, (u + Δu)
(v + Δv), can be interpreted as the area of
the large rectangle in the figure—provided
that Δu and Δv happen to be positive.
THE PRODUCT RULE

The change in the area of the rectangle
is:
( ) ( )( )
the sum of the three shaded areas
uv u u v v uv
u v v u u v
      
      

THE PRODUCT RULE Equation 1

If we divide by ∆x, we get:
( )
uv v u v
u v u
x x x x
   
   
   
THE PRODUCT RULE

If we let ∆x → 0, we get the derivative of uv:
 
0
0
0 0 0 0
( )
( ) lim
lim
lim lim lim lim
0.
x
x
x x x x
d uv
uv
dx x
v u v
u v u
x x x
v u v
u v u
x x x
dv du dv
u v
dx dx dx
 
 
       



  
 
   
 
  
 
  
 
     
  
 
  
THE PRODUCT RULE

 Notice that ∆u → 0 as ∆x → 0 since f
is differentiable and therefore continuous.
( )
d dv du
uv u v
dx dx dx
 
THE PRODUCT RULE Equation 2

Though we began by assuming (for the
geometric interpretation) that all quantities are
positive, we see Equation 1 is always true.
 The algebra is valid whether u, v, ∆u, and ∆v
are positive or negative.
 So, we have proved Equation 2—known as
the Product Rule—for all differentiable functions
u and v.
THE PRODUCT RULE

If f and g are both differentiable, then:
In words, the Product Rule says:
 The derivative of a product of two functions is
the first function times the derivative of the second
function plus the second function times the derivative
of the first function.
     
( ) ( ) ( ) ( ) ( ) ( )
d d d
f x g x f x g x g x f x
dx dx dx
 
THE PRODUCT RULE

a. If f(x) = xex, find f ’(x).
b. Find the nth derivative, f (n)(x)
THE PRODUCT RULE Example 1

By the Product Rule, we have:
THE PRODUCT RULE Example 1 a
'( ) ( )
( ) ( )
1
( 1)
x
x x
x x
x
d
f x xe
dx
d d
x e e x
dx dx
xe e
x e

 
  
 

Using the Product Rule again, we get:
''( ) ( 1)
( 1) ( ) ( 1)
( 1) 1
( 2)
x
x x
x x
x
d
f x x e
dx
d d
x e e x
dx dx
x e e
x e
 
 
 
   
   
 
THE PRODUCT RULE Example 1 b

Further applications of the Product Rule
give:
4
'''( ) ( 3)
( ) ( 4)
x
x
f x x e
f x x e
 
 

In fact, each successive differentiation
adds another term ex.
So:
( ) ( )
n x
f x x n e
 

Differentiate the function
( ) ( )
f t t a bt
 

Using the Product Rule, we have:
THE PRODUCT RULE E. g. 2—Solution 1
 
1 2
1
2
'( ) ( ) ( )
( )
( ) ( 3 )
2 2
d d
f t t a bt a bt t
dt dt
t b a bt t
a bt a bt
b t
t t

   
    
 
  

If we first use the laws of exponents to
rewrite f(t), then we can proceed directly
without using the Product Rule.
 This is equivalent to the answer in Solution 1.
1 2 3 2
1 2 1 2
3
1
2 2
( )
'( )
f t a t bt t at bt
f t at bt

   
 
THE PRODUCT RULE E. g. 2—Solution 2

Example 2 shows that it is sometimes easier
to simplify a product of functions than to use
the Product Rule.
In Example 1, however, the Product Rule is
the only possible method.
THE PRODUCT RULE

If , where
g(4) = 2 and g’(4) = 3, find f’(4).
( ) ( )
f x xg x


Applying the Product Rule, we get:
So,
 
1 2
1
2
'( ) ( ) ( ) ( )
( )
'( ) ( ) '( )
2
d d d
f x xg x x g x g x x
dx dx dx
g x
xg x g x x xg x
x

   
  
   
    
(4) 2
'(4) 4 '(4) 2 3 6.5
2 2
2 4
g
f g
     


We find a rule for differentiating the quotient
of two differentiable functions u = f(x) and
v = g(x) in much the same way that we found
the Product Rule.
THE QUOTIENT RULE

If x, u, and v change by amounts Δx, Δu,
and Δv, then the corresponding change
in the quotient u / v is:
   
   
u u u u
v v v v
u u v u v v v u u v
v v v v v v
 
 
  
 
 
 
       
 
   
THE QUOTIENT RULE

So,
 
 
0
0
lim
lim
x
x
u v
d u
dx v x
u v
v u
x x
v v v
 
 

 

 

 
 

 

 
THE QUOTIENT RULE

As ∆x → 0, ∆v → 0 also—because v = g(x)
is differentiable and therefore continuous.
Thus, using the Limit Laws, we get:
 
0 0
2
0
lim lim
lim
x x
x
u v du dv
v u v u
d u x x dx dx
dx v v v v v
   
 
 
 
   
 
 
 
 
THE QUOTIENT RULE

If f and g are differentiable, then:
In words, the Quotient Rule says:
 The derivative of a quotient is the denominator times
the derivative of the numerator minus the numerator
times the derivative of the denominator, all divided by
the square of the denominator.
   
2
( ) ( ) ( ) ( )
( )
( ) ( )
d d
g x f x f x g x
d f x dx dx
dx g x g x

 

   
   
THE QUOTIENT RULE

The Quotient Rule and the other
differentiation formulas enable us to
compute the derivative of any rational
function—as the next example illustrates.
THE QUOTIENT RULE

Let
2
3
2
6
x x
y
x
 


THE QUOTIENT RULE Example 4

Then,
       
 
     
 
   
 
 
3 2 2 3
2
3
3 2 2
2
3
4 3 4 3 2
2
3
4 3 2
2
3
6 2 2 6
'
6
6 2 1 2 3
6
2 12 6 3 3 6
6
2 6 12 6
6
d d
x x x x x x
dx dx
y
x
x x x x x
x
x x x x x x
x
x x x x
x
      


    


     


    



Find an equation of the tangent
line to the curve y = ex / (1 + x2)
at the point (1, ½e).

According to the Quotient Rule,
we have:
     
 
   
 
 
 
2 2
2
2
2
2
2 2
2 2
1 1
1
1 2 1
1 1
x x
x x x
d d
x e e x
dy dx dx
dx x
x e e x e x
x x
  


  
 
 

So, the slope of the tangent line at
(1, ½e) is:
 This means that the tangent line at (1, ½e)
is horizontal and its equation is y = ½e.
1
0
x
dy
dx 


In the figure, notice that the function
is increasing and crosses its tangent line
at (1, ½e).

Don’t use the Quotient Rule every
time you see a quotient.
 Sometimes, it’s easier to rewrite a quotient first
to put it in a form that is simpler for the purpose
of differentiation.
NOTE

For instance, though it is possible to
differentiate the function
using the Quotient Rule, it is much easier
to perform the division first and write
the function as
before differentiating.
2
3 2
( )
x x
F x
x


1 2
( ) 3 2
F x x x
 
NOTE

Here’s a summary of the differentiation
formulas we have learned so far.
     
     
 
1
'
2
0
' ' ' ' ' ' ' '
' '
' ' '
n n x x
d d d
c x nx e e
dx dx dx
cf cf f g f g f g f g
f gf fg
fg fg gf
g g

  
      
  
  
 
 
DIFFERENTIATION FORMULAS

Lec5_Product & Quotient Rule.ppt

More Related Content

What's hot

Similar to Lec5_Product & Quotient Rule.ppt

Recently uploaded

Lec5_Product & Quotient Rule.ppt