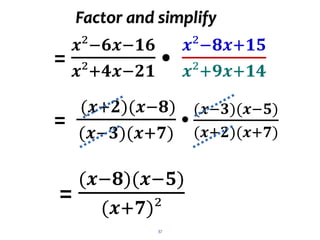This document provides instruction on operations of functions, including addition, subtraction, multiplication, and division. It begins by explaining how to add and subtract functions by applying the functions to the variable x. For addition, (f+g)(x) is defined as f(x) + g(x), and for subtraction, (f-g)(x) is defined as f(x) - g(x). It then covers multiplying functions by defining the product (f⋅g)(x) as f(x)⋅g(x) and dividing functions by defining the quotient (f/g)(x) as f(x)/g(x) where g(x) cannot be zero. Examples

1. 1

2. Lesson 3a: Operations on Functions
[Addition and Subtraction]
F I R S T Q U A R T E R
Chapter 1: Functions
perform addition and subtraction of
functions
solve problems involving addition
and subtraction of functions
At the end of this lesson, learner should be able to:
Objective

3. 3
Before we proceed with
this lesson, you should be able to recall
addition and subtraction of like and
unlike terms.
In adding and subtracting like
terms, or subtract the
numerical coefficients of the given
terms following the rules on
adding and subtracting integers,
then copy the literal coefficient.

4. 4
 To add 5x and 8x:
5x + 8x = (5+8)x = 13x
Note: You cannot add or subtract unlike terms.
Example: 5x + 5x² and 3x² − 5x
To subtract 5x and 8x:
5x − 8x = (5−8)x = −3x

5. 5
1. Addition: Rule A. To add numbers with
the same sign, add their absolute values or
magnitudes and affix the common sign.
1] 12 + 22 = 34
2] -12 + (-22) = -34
3] -25.3 + (4.9) = -20.4

6. 6
Example 3. Find the sum of
𝟏
𝟑
+
𝟐
𝟓
Solution. The LCD of the two
fractions is 15.
𝟏
𝟑
+
𝟐
𝟓
=
=
𝟓+𝟔
𝟏𝟓
𝟓
𝟏𝟓
+
𝟔
𝟏𝟓
=
𝟏𝟏
𝟏𝟓

7. 7
Rule B. To add numbers with unlike signs,
get the difference of their absolute values
or magnitudes and affix the sign of the
number having the greater absolute values.
Example 4. 85+ (-32) = 53
Example 5. -25.3 + (4.9) = -20.4

8. 235
– 112
8
2. Subtraction: Rule. To subtract one signed
number from another signed number, just
change the sign of the subtrahend then
proceed to algebraic addition.
Example 1. Find the difference of
123

9. 9
Example 2. Find the difference of
3.59
– - 8.53
12.12

10. 10
Example 3. 23x
- -25x
the of the subtrahend shall be changed, then
proceed to algebraic addition.
48x
23x
+25x

11. 11
Addition and Subtractions of Fractions:
(a) Find the least common denominator
(LCD) of both fractions.
(b) Rewrite the fractions as equivalent
fractions with the same LCD.
(c) The LCD is the denominator of the
resulting fraction.
(d) The sum or difference of the
numerators is the numerator of the
resulting fraction.

12. 12
𝟏
𝒙−𝟑
+
𝟐
𝒙−𝟓
Example. Find the sum of
𝟏
𝒙−𝟑
and
𝟐
𝒙−𝟓
Solution. The LCD of the two rational
expressions is (x-3)(x-5) or (x²-8x+15).
=
𝒙−𝟓 +𝟐𝒙−𝟔
𝐱²−𝟖𝐱+𝟏𝟓
=
𝟑𝒙−𝟏𝟏
𝐱²−𝟖𝐱+𝟏𝟓
=
𝟏 𝒙−𝟓 + 𝟐(𝒙−𝟑)
(x−3)(x−5)

13. 13
The important concept that need to
understand in this lesson is that
adding and subtracting two or more
functions together will result in
another function. Dividing two
functions together will also result
in another function if the
denominator or divisor is not the
zero function.

14. 14
(b) Their difference, denoted by f - g, is
the function defined by:
Definition. Let f and g be functions.
(a) Their sum, denoted by f + g, is the
function defined by:
(f + g)(x) = f(x) + g(x)
(f - g)(x) = f(x) - g(x)

15. 15
 Addition of Functions
Given two functions f(x) and
g(x), their sum, denoted by
(f+g)(x), is the function defined
by
(f+g)(x)=f(x)+g(x)

16. 16
 Subtraction of Functions
Given two functions f(x) and
g(x), their difference, denoted
by (f-g)(x), is the function
defined by
(f-g)(x)=f(x)-g(x)
Note: We enclose f+g and f−g with ( ) to show
that they both work on x.

17. 17
Given the functions
f(x)=4x²+3x+2 and
g(x)=7x²−5x−1.
find (f+g)(x) and
(f−g)(x).

18. 18
Step 1: Identify the formula needed
to solve the problem.
Step 2: Substitute the given
functions to the formula.
Step 3: Simplify.
Given the functions f(x)=4x²+3x+2 and
g(x)=7x²−5x−1, find (f+g)(x) and (f−g)(x).

19. 19
Step 1: Identify the formula
needed to solve the
problem.
(f + g)(x) = f(x) + g(x)
Given the functions
f(x)=4x²+3x+2 and g(x)=7x²−5x−1,
find (f + g)(x).
 rule of of function

20. 20
Step 2: Substitute the
given functions to the
formula.
(f+g)(x) = (4x²+3x+2) +
(7x²−5x−1)
Given the functions f(x)=4x²+3x+2
and g(x)=7x²−5x−1, find (f + g)(x).

21. 21
Step 3: Simplify.
(f+g)(x) = (4x²+3x+2) + (7x²−5x−1)
(f+g)(x) = 4x² +3x + 2 + 7x² − 5x − 1
(f+g)(x) = 4x²+7x² + 3x − 5x + 2 − 1
(f+g)(x) = 11x² − 2x + 1
distributive property
of multiplication

22. 22
Step 1: Identify the formula needed to
solve the problem.
(f-g)(x)=f(x) - g(x) rule of of function
Step 2: Substitute the given functions to
the formula.
(f-g)(x) = (4x²+3x+2) (7x²−5x−1)
Given the functions f(x)=4x²+3x+2
and g(x)=7x²−5x−1, find (f - g)(x).

23. 23
Step 3: Simplify.
(f-g)(x) = (4x²+3x+2) - (7x²−5x−1)
(f-g)(x) = 4x² +3x + 2 - 7x² + 5x + 1
(f-g)(x) = 4x²-7x² + 3x + 5x + 2 + 1
(f-g)(x) = 3x² + 8x + 3
distributive property
of multiplication

24. F I R S T Q U A R T E R
Chapter 1: Functions
Lesson 3b: Operations on Functions
[Multiplication and Division]
 multiply and divide functions
 solve problems involving
multiplication and division of
functions
Objective At the end of this lesson, learner should be able to:

25. 3. Multiplication:
(a) Rewrite the numerator and
denominator in terms of its prime
functions.
(b) Common factors in the
numerator and denominator can be
simplified as (this is often called
cancelling).
33

26. 3. Multiplication:
(c) Multiply the numerators
together to get the new
numerator.
(d) Multiply the denominators
together to get the new
denominator.
34

27. 35
4. Division:
To divide two fractions or
rational expressions,
multiply the dividend with
the reciprocal of the
divisor.

28. 36
𝒙²−𝟔𝒙−𝟏𝟔
𝒙²+𝟒𝒙−𝟐𝟏
÷ 𝒙²+𝟗𝒙+𝟏𝟒
𝒙²−𝟖𝒙+𝟏𝟓 𝑎
𝑏
𝑐
𝑑
=
𝑎
𝑏
•
𝑑
𝑐
Example 5. Find the quotient of
𝒙²−𝟔𝒙−𝟏𝟔
𝒙²+𝟒𝒙−𝟐𝟏
÷
𝒙²+𝟗𝒙+𝟏𝟒
𝒙²−𝟖𝒙+𝟏𝟓
Solution. Multiply the dividend with the reciprocal of the
divisor. Express the numerators and denominators of the
two rational expression into their prime factors. Multiply
and cancel out common factors in the numerator and the
denominator to reduce the final answer to lowest terms.
=
𝒙²−𝟔𝒙−𝟏𝟔
𝒙²+𝟒𝒙−𝟐𝟏
•
𝒙²−𝟖𝒙+𝟏𝟓
𝒙²+𝟗𝒙+𝟏𝟒

29. 37
=
(𝒙+𝟐)(𝒙−𝟖)
(𝒙−𝟑)(𝒙+𝟕)
•
(𝒙−𝟑)(𝒙−𝟓)
(𝒙+𝟐)(𝒙+𝟕)
=
𝒙²−𝟔𝒙−𝟏𝟔
𝒙²+𝟒𝒙−𝟐𝟏
•
𝒙²−𝟖𝒙+𝟏𝟓
𝒙²+𝟗𝒙+𝟏𝟒
=
(𝒙−𝟖)(𝒙−𝟓)
(𝒙+𝟕)²
Factor and simplify

30. 38
Before you proceed with this
lesson, you should be able to recall addition and
subtraction of functions, and the laws of exponents.
No, because when multiplying terms
with the same bases, we simply copy
the base and add the exponents.
Therefore, x² • x⁴ = x⁶
1. Is the expression x² • x⁴ the same
as x⁸ ? Why or why not?

31. Yes, because when dividing terms with
the same bases, we simply copy the
base and subtract the exponents.
Therefore,
𝒙𝟓
𝒙𝟐 = 𝒙𝟑
39
Before we proceed with this lesson, you should
be able to recall addition and subtraction of
functions, and the laws of exponents.
Is the expression
𝒙𝟓
𝒙𝟐 the same as 𝒙𝟑
?
Why or why not?

32. 40
Given the two functions f(x)
and g(x) , their product,
denoted by f•g(x), is the
function defined by
Multiplication of Functions
f•g(x) = f(x) • g(x)

33. 41
Given the two functions f(x) and g(x) ,
their quotient, denoted by
𝒇
𝒈
𝒙 , is
the function defined by
In this case, g(x) cannot be zero because if
an expression is divided by zero, it will be
.
Division of Functions
𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)
where g(x)≠0.

34. 42
Given the functions
f(x)=x²−1
and g(x)=x+1
Multiplication & Division of Functions

35. 43
Step 1: Identify the formula
needed to solve the problem.
f(x)=x²−1 g(x)=x+1
Multiplication of Functions
(f•g)(x) = f(x) • g(x)
Given the functions

36. 44
Step 2: Substitute the
given functions to the
formula.
(f•g)(x) = f(x) • g(x)
(f•g)(x) = (x²−1)( x+1)
f(x)=x²−1 g(x)=x+1

37. 45
Step 3: Simplify.
(f•g)(x) = (x²)(x) + (x²)(1) +
(−1)(x) + (−1)(1)
(f•g)(x) = x³ + x² − x − 1
(f•g)(x) = (x²−1)( x+1)

38. 46
Step 1: Identify the formula
needed to solve the problem.
f(x)=x²−1 g(x)=x+1
Division of Functions
Given the functions
𝒇
𝒈
𝒙 =
𝒇(𝒙)
𝒈(𝒙)

39. 47
Step 2: Substitute the given
functions to the formula.
f(x)=x²−1 g(x)=x+1
𝒇
𝒈 𝒙 =
𝒇(𝒙)
𝒈(𝒙)
𝒇
𝒈 𝒙 =
𝒙²−𝟏
𝒙 +𝟏

40. 48
Step 3: Simplify.
𝒇
𝒈
𝒙 =
𝒙²−𝟏
𝒙 + 𝟏
By Factoring
the numerator
𝒇
𝒈
𝒙 =
(𝒙+𝟏)(𝒙−𝟏)
𝒙+𝟏
𝒇
𝒈
𝒙 = 𝒙 − 𝟏
Cancel out
similar terms

41. 55
When dividing functions, the
order of the functions is
important. Generally, (
𝒉
𝒈
)(x)
is different from (
𝒈
𝒉
)(x) if
h(x)≠g(x).

42. 56
The product of two functions f(x) and
g(x) is defined by (f⋅g)(x)=f(x)⋅g(x).
The quotient of two functions f(x) and
g(x) is defined by (
𝒇
𝒈
)(x)=
𝒇(𝒙)
𝒈(𝒙)
where
g(x)≠0.
The inequality g(x)≠0 means that g(x) can
never be zero because dividing an
expression by zero is undefined.

43. End of Lesson 3a & 3b
THANK YOU for your
60 minutes Dear
Students!
57
If you don’t fight for what you
want, don’t cry for what you
lost…