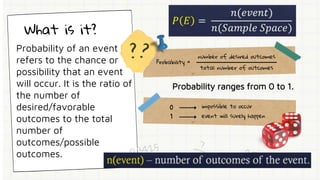
The document discusses probability and provides examples of calculating the probability of simple events. It defines probability as the ratio of favorable outcomes to total possible outcomes. Examples include calculating the probability of drawing certain cards, rolling certain numbers on a die, and selecting particular items from sets. The document also covers determining the probability of complementary events and expresses probabilities as fractions, decimals, and percentages.

1. Probability of
Simple Event

2. Objectives:
• Illustrate probability of
simple events.
• Find the probability of
simple events.

3. Lesson Outline
Here's an overview of today's lesson.
• Understanding Probability
• Determining Probability of Simple
Events
• Describing Probability using
Fraction, Decimals, and Percentage

4. What is it?
Probability of an event
refers to the chance or
possibility that an event
will occur. It is the ratio of
the number of
desired/favorable
outcomes to the total
number of
outcomes/possible
outcomes.
Probability =
number of desired outcomes
total number of outcomes
Probability ranges from 0 to 1.
impossible to occur
event will surely happen

5. Properties of Probability of an Event
1. A probability is a number between 0 and 1, inclusive.
The closer the probability of an event to 1, the
more likely the event to happen and the closer the
probability of an event to zero, the less likely to
happen.
2. The probability of an event that cannot happen is 0.
3. The probability of an event that must happen is 1.
4. The probability of an event E is P, then the
probability of the compliment of E is 1 – P.

6. Example 1:
A coin is tossed. Find the probability of getting a head.
n(S) = 𝟐
Sample Space = 𝑯, 𝑻
n(E) = 𝑯
Event = 𝑯
P(E) =
𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝑬 𝒏(𝑬)
𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝑺 𝒏(𝑺)
P(head) =
1
2
= 𝟓𝟎% = 𝟎. 𝟓

7. Example 2:
What is the probability of rolling a prime number on a
number cube?
n(S) = 6
Sample Space = 1, 2, 3, 4, 5, 6
n(E) = 3
Event = 2, 3, 5
P(head) =
3
6
=
1
2
P(E) =
𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝑬 𝒏(𝑬)
𝒏𝒖𝒎𝒃𝒆𝒓 𝒐𝒇 𝒆𝒍𝒆𝒎𝒆𝒏𝒕𝒔 𝒊𝒏 𝑺 𝒏(𝑺)

8. A standard deck of cards has four suits: hearts, clubs,
spades, diamonds. Each suite has thirteen cards: ace, 2, 3, 4,
5, 6, 7, 8, 9, 10, jack, queen and king. Thus, the entire deck
has 52 cards total.

9. Example 3:
A playing card is drawn at random from a standard
deck of 52 playing cards. Find the probability of
drawing
a. a diamond
b. a black card
c. a queen
P(a diamond) =
𝑛(𝐸)
𝑛(𝑆)
=
13
52
=
𝟏
𝟒
P(a black card) =
𝑛(𝐸)
𝑛(𝑆)
=
26
52
=
𝟏
𝟐
P(a queen) =
𝑛(𝐸)
𝑛(𝑆)
=
4
52
=
𝟏
𝟏𝟑

10. Example 4:
Three coins are tossed. What is the probability of
getting
a. three heads?
b. two heads?
c. one head?
d. at least two tails?
e. at most two tails?
f. no tail?
P(E) =
𝑛(𝐸)
𝑛(𝑆)
=
8
𝟏
𝟖
𝟑
𝟖
𝟑
𝟖
𝟒
𝟖 = ½
𝟕
𝟖
𝟏
𝟖

11. Example 5:
A bag contains 7 white balls and 11 orange balls.
a. If a ball is drawn at random from the bag, find
the probability that
i. green ii. white iii. not white
b. If 12 red balls are added to the bag and a ball
is drawn at random from the bag, find the
probability that
i. red ii. not red
iii. orange
P(E) =
𝑛(𝐸)
𝑛(𝑆)
=
18
0
𝟕
𝟏𝟖
𝟏𝟏
𝟖
𝟏𝟖
𝟑𝟎 = 3/5
= 𝟏𝟏
𝟑𝟎
𝟏𝟐
𝟑𝟎 = 2/5

12. Example 6:
Find the probability of the complement of each event.
a. Rolling a die and getting a 4..
b. Selecting a letter of the alphabet and getting a
vowel.
b. Selecting a month and getting a month that begins
with a J
𝑷 𝟒 = 𝟏
𝟔 1 - 𝟏
𝟔 = 𝟓/𝟔
𝑷 𝒗𝒐𝒘𝒆𝒍 = 𝟓
𝟐𝟔
1 - 𝟓
𝟐𝟔 = 𝟐𝟏/𝟐𝟔
𝑷 𝑱 = 𝟑
𝟏𝟐 =
𝟏
𝟒 1 - 𝟏
𝟒 =
𝟑
𝟒

13. Thank you!