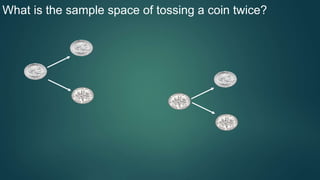
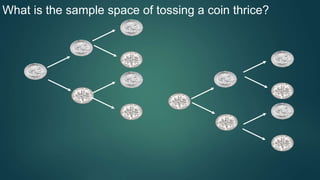
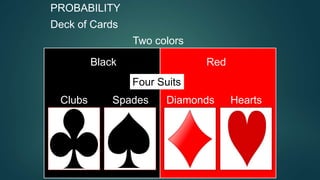
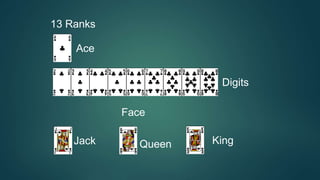
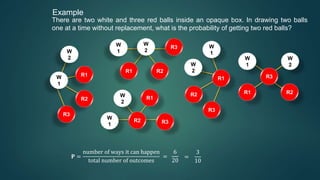
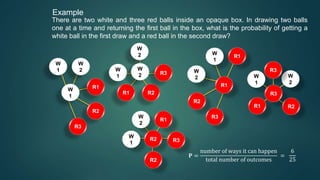
* There are 15 red balls
* Let w = number of white balls
* Let g = number of green balls
* Total balls = 15 + w + g = 30
* Probability of white ball = w/30
* Probability of green ball = g/30
* Given: Probability of white ball is twice the probability of green ball
* So: w/30 = 2g/30
* Solving the above equation we get: w = 2g
* Substituting w = 2g in the equation: 15 + w + g = 30
* 15 + 2g + g = 30
* 18g = 15
* g = 5
* w = 2g = 2 * 5 = 10