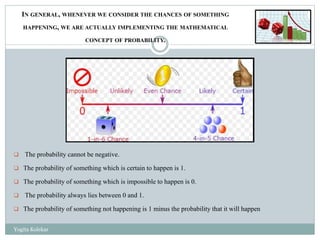
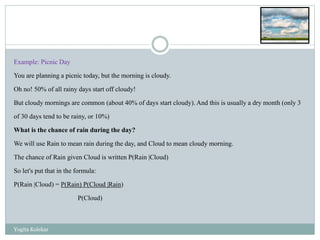
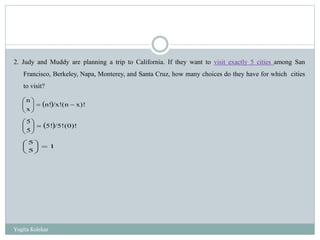
The document outlines fundamental concepts of probability, including definitions, rules, events, conditional probability, and real-life applications. It explains crucial probability rules such as the addition and multiplication rules, along with examples like drawing cards and rolling dice. Additionally, it discusses Bayes' theorem and the significance of probability in various fields like insurance, weather forecasting, and sports strategy.

1. THE PROBABILITY
LIFE SAVER
Yogita Kolekar

2. AGENDA
 Basic concepts of probability.
 What is mean by probability?
 Probability & its importance in real life.
 Concept of events.
 Probability Rules
 Events
 Conditional Probability
 Bayes’ Theorem
 Permutation and Combination
 Real Life Applications
Yogita Kolekar

3. BASIC CONCEPTS OF PROBABILITY
 Experiment: A measurement process that produces quantifiable results (e.g. throwing two dice, dealing
cards, measuring heights of people)
 Outcome: a single result from a measurement (e.g. the numbers shown on the a dice)
 Sample space (S): the set of all possible outcomes from an experiment (e.g. the set of all possible five-
card hands)
 The number of all possible outcomes may be:
(a) Finite (e.g. all possible outcomes from throwing a single die; all possible outcome from tossing of a
coin)
(b) Countably infinite (e.g. number of proton-proton events to be made before a Higgs boson event is
observed) or
(c) Continuous (e.g. heights of people)
Yogita Kolekar

4. PROBABILITY
 Probability is the likelihood or chance of an event occurring.
 Probability = The number of ways of achieving success
The total number of possible outcomes
 It is associated with discrete variables.
 The probability of any event is the number of times or ways an event can occur (m) divided by the total
number of possible associated events (N): P(E)=m/N
 For example, if we toss a fair coin, there are only two possible outcomes (a head or a tail). The
likelihood that one event, for example a tail, is 1/2 or p(T) = 0.5
P (Tail) = 1/2 = 0.5
 The proportion of tails is 0.5 or there is a 50% chance of tossing a tail or 50% of the time we would
expect a tail to result from a toss of a fair coin
Yogita Kolekar

5.  The probability cannot be negative.
 The probability of something which is certain to happen is 1.
 The probability of something which is impossible to happen is 0.
 The probability always lies between 0 and 1.
 The probability of something not happening is 1 minus the probability that it will happen
IN GENERAL, WHENEVER WE CONSIDER THE CHANCES OF SOMETHING
HAPPENING, WE ARE ACTUALLY IMPLEMENTING THE MATHEMATICAL
CONCEPT OF PROBABILITY.
Yogita Kolekar

6.  P(A) is read as 'the probability of A', where A is an event we are interested in.
 P(A|B) is read as 'the probability of A given B occurs'.
 P(not A) is read as 'the probability of not A ', or 'the probability that A does not occur'.
B: Getting an odd number
B: {1,3,5}
n(B) = 3
P(B) = n(B)/n(S) = 3/6 = 1/2 = 0.5
 Example:
Rolling of a die
Sample space (S) = { 1,2,3,4,5,6 }
n(S) = 6
A: Getting an even number
A: {2,4,6}
n(A) = 3
P(A) = n(A)/n(S) = 3/6 = 1/2 = 0.5
Yogita Kolekar

7. Consider, another example:
Tossing of a coin
Sample space (S) = { H, T }
n(S) = 2
A: Getting a head
A: {H}
n(A) = 1
P(A) = n(A)/n(S) = 1/2 = 0.5
Yogita Kolekar

8. PROBABILITY AND ITS IMPORTANCE IN
REAL LIFE
Probability is the study of random events.
 It is used in analyzing games of chance, genetics, weather prediction, and a myriad of other everyday
events.
 Card Games: Traditional card game of skills ‘rummy’ uses the concept of probability, along with those
of permutations and combinations. Players keep on calculating their chances of getting a particular card
they require and in the process learn these concepts without making conscious efforts.
 Video Games and Board Games: On the same lines, these games too propel the player to think in terms
of probability.
 Typing on smart devices: When we type, the software constantly keeps suggesting words. It does this
using probability- depending on which word is how commonly used.
Yogita Kolekar

9.  Sports: To decide what are the chances of winning or losing of a particular team based on their previous
record. Similarly, probability is put to use in order to devise the sports strategy also. For instance, by
tracking the record of a batsman in cricket, it is decided at what place or rank, he should play.
 Weather forecasting: The meteorological department makes use of the concept of probability for their
work. However, common people also make use of the concept. You notice for a few days that clouds
come up but it does not rain. Next time when you are about to step out, you think it over in your mind
and decide there is no need to carry an umbrella.
 Insurance policies: When you get anything insured, you study which insurance policy would be
appropriate depending on your usage of the thing and/or what are the chances of damage and what kind
of damage is possible.
For example - few people opt for fire insurance of their property because they perceive that odds are low,
but of lately a lot of people have started getting their expensive smart phones insured because their
chances of getting damaged or lost are high.
Yogita Kolekar

10. PROBABILITY RULES
There are three main rules associated with basic probability: the addition rule, the multiplication rule, and the
complement rule.
1) The Addition Rule:
P(A or B) = P(A) + P(B) - P(A and B)
If A and B are mutually exclusive events, or those that cannot occur together, then the third term is 0,
and the rule reduces to P(A or B) = P(A) + P(B).
For example, you can't flip a coin and have it come up both heads and tails on one toss.
Consider pack of playing cards, what is the probability of drawing either a queen or a heart card.
P(Queen or Heart) = P(Queen) + P(Heart) - P(Queen and Heart)
P(Queen or Heart) = 4/52 + 13/52 - 1/52
P(Queen or Heart) = 16/52
Yogita Kolekar

11. 2) The Multiplication Rule:
P(A and B) = P(A) * P(B|A) or P(B) * P(A|B)
If A and B are independent events, we can reduce the formula to P(A and B) = P(A)* P(B). The term
independent refers to any event whose outcome is not affected by the outcome of another event. For
instance, consider the second of two coin flips, which still has a 0.50 (50%) probability of landing heads,
regardless of what came up on the first flip.
What is the probability that, during the two coin flips, you come up with tails on the first flip and heads
on the second flip?
Let's perform the calculations: P = P(tails) * P(heads) = (0.5) * (0.5) = 0.25
For example what is the probability of drawing a card which is both a queen and a heart?
P(Queen and Heart) = 1/52
i.e., P(Queen and Heart) = P(Queen) * P(Heart) = 1/4 * 1/13 = 1/52
Yogita Kolekar

12. 3) The Complement Rule:
P(not A)/ P(A’) = 1 - P(A)
Do you see why the complement rule can also be thought of as the subtraction rule? This rule builds upon
the mutually exclusive nature of P(A) and P(not A). These two events can never occur together, but one
of them always has to occur. Therefore P(A) + P(not A)= 1.
For example, if the weatherman says there is a 0.3 chance of rain tomorrow, what are the chances of no
rain?
Let's do the math: P(no rain) = 1 - P(rain) = 1 - 0.3 = 0.7
Yogita Kolekar

13. EVENTS
 An event is any subset of a sample space (including the empty set, and the whole set)
 Single Events
1. Example
There are 6 beads in a bag, 3 are red, 2 are yellow and 1 is blue. What is the probability of picking a
yellow?
The probability is the number of yellows in the bag divided by the total number of balls, i.e. 2/6 = 1/3.
2. Example
There is a bag full of coloured balls, red, blue, green and orange. Balls are picked out and replaced. John
did this 1000 times and obtained the following results:
Number of blue balls picked out: 300
Number of red balls: 200
Number of green balls: 450
Number of orange balls: 50
Yogita Kolekar

14. a) What is the probability of picking a green ball?
For every 1000 balls picked out, 450 are green. Therefore P(green) = 450/1000 = 0.45
b) If there are 100 balls in the bag, how many of them are likely to be green?
The experiment suggests that 450 out of 1000 balls are green. Therefore, out of 100 balls, 45 are green
(using ratios).
3. Playing Cards:
A man chooses a card at random from a pack of playing cards. What is the probability that the card is a
Queen?
Total cards = 52
Red cards = 26 and Black cards = 26
P(Card is a Queen) = 4/52 = 1/13
Yogita Kolekar

15.  Multiple Events
Independent and Dependent Events
 Independent Events
Suppose now we consider the probability of 2 events happening. For example, we might throw 2 dice
and consider the probability that both are 6's.
We call two events independent if the outcome of one of the events doesn't affect the outcome of
another.
For example, if we throw two dice, the probability of getting a 6 on the second die is the same, no matter
what we get with the first one- it's still 1/6.
Yogita Kolekar

16.  Dependent Events
When the probability of one event depends on another, the events are dependent.
The calculations for dependent events are similar to those for mutually exclusive events. Of course, we
have to consider how one event affects the next.
What is the probability of drawing two from a standard deck of cards without replacement? First, the
probability of drawing the first queen is
P(Q1) = 4 ÷ 52 = 0.077
But the probability of drawing a second queen is different because now there are only three queens and
51 cards.
P(Q2) = 3 ÷ 51 = 0.059
The probability is still the product of the two probabilities
P(Q1, Q2) = 0.077 x 0.059 = 0.0045
Yogita Kolekar

17.  Mutually exclusive events:
If two events are mutually exclusive, it means that they cannot occur at the same time.
For example, the two possible outcomes of a coin flip are mutually exclusive; when you flip a coin, it
cannot land both heads and tails simultaneously.
Rolling of a die
Sample space (S) = { 1,2,3,4,5,6 }
n(S) = 6
A: Getting an even number
A: {2,4,6}
n(A) = 3
P(A) = n(A)/n(S) = 3/6 = 1/2 = 0.5
B: Getting an odd number
B: {1,3,5}
n(B) = 3
P(B) = n(B)/n(S) = 3/6 = 1/2 = 0.5
P(A and B) = P(A) x P(B) = 0.5 x 0.5
P(A and B) = 0.25
Yogita Kolekar

18. CONDITIONAL PROBABILITY
A conditional probability is one in which some condition has already been met or given to us.
If events A and B are not independent, then the probability of the intersection of A and B (the probability
that both events occur) is defined by,
P(A and B) = P(A)* P(B/A)
From this definition, the conditional probability P(B|A) is easily obtained by dividing by P(A):
P(B/A) = P(A and B)/ P(A)
Similarly, the conditional probability P(A|B) is,
P(A/B) = P(A and B)/ P(B)
To introduce the concept of conditional probability, let’s consider two events, A and B:
A = it rains
B = a Cricket League match is cancelled
Yogita Kolekar

19. From these definitions, you might quickly realize that the two events are not mutually exclusive; that is,
both A and B could occur simultaneously.
Also, the two events are likely not independent of one another; that is to say, if event A occurs (it rains), it
will likely impact the probability of B occurring (the event of rain will greatly increase the likelihood that
the Cricket League match is cancelled).
So, what is the probability that the Cricket League match is cancelled, given that it rains today?
This probability is called a conditional probability, because we are given the condition that it is raining.
In other words, event B is no longer a “what if” - we know that it has occurred, and it may or may not
have an impact on the probability of event A(more on this soon). Therefore, “Given that event B has
already occurred, what is the probability of A?” is a conditional probability.
A = it rains
B = a Cricket League match is cancelled
Yogita Kolekar

20. For example, let’s assume we are drawing from a standard fifty-two card deck, and our goal is to draw
cards of the same suit. If the first card we draw is a spade (our given condition), what is the probability
that the next card will be a spade?
Since there are only twelve spades left in the deck, and only fifty-one cards left to draw from, our
conditional probability is 12/51
Note that this is different from the probability of drawing a spade from the original complete
deck&emdash;13/52.
Thus, when we are given a condition - in this case, that one spade had already been drawn - the
probabilities can change.
What is the probability of drawing a queen given that it is heart from the pack of playing cards?
P(Queen/ Heart) = P(A and B)/ P(B)
P(Queen/ Heart) = (1/52)/ (13/52)
P(Queen/ Heart) = 1/13
Yogita Kolekar

21. BAYES’ THEOREM
It is a way of finding a probability when we know certain other probabilities. Also we can say that, It is
a formula that describes how to update the probabilities of hypotheses when given evidence.
The formula is:
P(A/B) = P(A)*P(B/A)
P(B)
P(A/B) = Probability of A given B
P(B/A) = Probability of B given A
P(A) = Probability of event A occurs
P(B) = Probability of event B occurs
Yogita Kolekar

22. Example: Picnic Day
You are planning a picnic today, but the morning is cloudy.
Oh no! 50% of all rainy days start off cloudy!
But cloudy mornings are common (about 40% of days start cloudy). And this is usually a dry month (only 3
of 30 days tend to be rainy, or 10%)
What is the chance of rain during the day?
We will use Rain to mean rain during the day, and Cloud to mean cloudy morning.
The chance of Rain given Cloud is written P(Rain |Cloud)
So let's put that in the formula:
P(Rain |Cloud) = P(Rain) P(Cloud |Rain)
P(Cloud)
Yogita Kolekar

23. Given that,
P(Rain) is Probability of Rain = 10% = 0.1
P(Cloud |Rain) is Probability of Cloud, given that Rain happens = 50% = 0.5
P(Cloud) is Probability of Cloud = 40% = 0.4
Now, the probability of rain when it is given that the day is cloudy given by,
P(Rain |Cloud) = 0.1*0.5/ 0.4
P(Rain |Cloud) = 0.125
i.e., 12.5% chance of rain. Not too bad, let's have a picnic!
Yogita Kolekar

24. PERMUTATION & COMBINATION
 Permutation:
When the order does matter it is a Permutation.
It represent the number of possible ways objects can be arranged where order is important.
There are basically two types of permutation:
1. Permutations with Repetition:
These are the easiest to calculate.
When a thing has n different types ... we have n choices each time!
For example: choosing 3 of those things, the permutations are:
n × n × n ......... (n multiplied 3 times)
More generally: choosing r of something that has n different types, the permutations are:
n × n × ................. (r times)
Which is easier to write down using an exponent of r: n × n × ... (r times) = nr
Yogita Kolekar

25. We should really call this a "Permutation Lock"!
Formula :
Permutations with Repetition = nr
where n is the number of things to choose from,
and we choose r of them,
repetition is allowed,
and order matters.
Example:
1. In the lock above, there are 10 numbers to choose from (0,1,2,3,4,5,6,7,8,9) and we choose 3 of them:
10 × 10 × ... (3 times) = 103 = 1,000 permutations.
Yogita Kolekar

26. 2. BS Team: has 3 members and there are ten questions. How many possible ways are there for BS’s team to
step up to the dais and answer ML competition questions in a single meet?
There are three possible choices for the first question, and three possible choices for 2nd, resulting
in 32=9 possibilities for the first two questions. Since there are ten questions, the total number of possible
line-ups are 310 =59,049
3. Real-World Application: Ice Cream
The ice cream shop on the corner carries 27 flavours of ice cream, how many different 4-scoop cones can
be created there?
There are 27 flavours, so n=27. We are creating 4-scoop cones, so r=4.
Number of unique cones=274 =531,441
Yogita Kolekar

27. 2. Permutations without Repetition:
In this case, we have to reduce the number of available choices each time.
i.e., Without repetition our choices get reduced each time.
Easier way to calculate these permutations is to use the formula:
n p r = n!/ (n-r)!
where n is the number of things to choose from,
and we choose r of them,
no repetitions,
order matters.
1. How many different ways can you stack a scoop of chocolate ice cream, a scoop of pistachio ice cream, a
scoop of vanilla ice cream, and a scoop of strawberry ice cream onto an ice cream cone?
Here, 4 different flavours of ice-cream, without repetition so 4! = 24 ways we can stack scoop of ice-
cream onto an ice-cream cone.
Yogita Kolekar

28. 2. what order could 16 pool balls be in?
After choosing, say, number "14" we can't choose it again.
So, our first choice has 16 possibilities, and our next choice has 15 possibilities, then 14, 13, 12, 11, ... etc.
And the total permutations are:
16 × 15 × 14 × 13 × ... = 20,922,789,888,000
But maybe we don't want to choose them all, just 3 of them, and that is then:
16 × 15 × 14 = 3,360
Their is another way to calculate permutations of 3 out of 16 pool balls,
n p r = n!/ (n-r)!
16 p3 = 16!/ (16-3)! = 16!/ 13!
16 p3 = 16*15*14
16 p3 = 3360
Yogita Kolekar

29. 3. How many different orders (arrangements) can be assigned to five sample of capsules in a row (capsules
A,B,C,D, and E)?
Order of arrangements for five capsules are, n! = 5! = 5*4*3*2*1 = 120 possible arrangements.
In the above example how many possible ways could three of the five capsules be arranged?
n p r = n!/ (n-r)!
5 p 3 = 5!/ (5-3)! = 5!/ 2!
5 p 3 = 5*4*3
5 p 3 = 60 possible ways to arrange order of capsules 3 out of five.
Yogita Kolekar

30. Combination:
When the order doesn't matter, it is a Combination.
"My fruit salad is a combination of apples, grapes and bananas" We don't care what order the fruits are
in, they could also be "bananas, grapes and apples" or "grapes, apples and bananas", its the same fruit
salad.
There are also two types of combinations
1. Combinations with Repetition:
Order does not matter and we can repeat as well.
Easier way to calculate combination with repetition is,
where n is the number of things to choose from,
and we choose r of them , repetition allowed,
order doesn't matter.
  1)!(n/r!!1nr
r
1nr





 
Yogita Kolekar

31. There are five flavors of ice-cream: banana, chocolate, lemon, strawberry and vanilla.
We can have three scoops. How many variations will there be?
Let's use letters for the flavors: {b, c, l, s, v}. Example selections include
 {c, c, c} (3 scoops of chocolate)
 {b, l, v} (one each of banana, lemon and vanilla)
 {b, v, v} (one of banana, two of vanilla)
There are n=5 things to choose from, and we choose r=3 of them. Order does not matter, and we can repeat!
There are 35 ways of having 3 scoops from five flavors of ice-cream.
  1)!(n/r!!1nr
r
1nr





 
  1)!(5/3!!153
3
153





 
35
3
153





 
Yogita Kolekar

32. 2. Combinations without Repetition:
A combination without repetition of x objects from n is a way of selecting x objects from a list of n.
Order does not matter. Each object can be selected only once.
A combination without repetition is also called a simple combination or, simply, a combination.
Easier way to calculate combination without repetition is,
where n is the number of things to choose from,
and we choose x of them,
no repetition,
order doesn't matter.
  x)!(n/x!n!
x
n






Yogita Kolekar

33. 1. How many ways can three different appetizers be chosen from a menu that has 10 choices?
Order does not matter and each object can be selected only once.
There are 120 ways , three different appetizers can choose menu from 10 choices.
  x)!(n/x!n!
x
n






  3)!(10/3!10!
3
10






120
3
10






Yogita Kolekar

34. 2. Judy and Muddy are planning a trip to California. If they want to visit exactly 5 cities among San
Francisco, Berkeley, Napa, Monterey, and Santa Cruz, how many choices do they have for which cities
to visit?
  x)!(n/x!n!
x
n






  (0)!/5!5!
5
5






1
5
5






Yogita Kolekar

35. Yogita Kolekar