Recommended
PDF
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
PDF
PDF
PDF
PPTX
PPTX
PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半
PDF
PRML ベイズロジスティック回帰 4.5 4.5.2
PDF
PPTX
PDF
PPTX
PDF
PDF
PPTX
多項式あてはめで眺めるベイズ推定�~今日からきみもベイジアン~�
PDF
PDF
DARM勉強会第3回 (missing data analysis)
PDF
PDF
PRML復々習レーン#2 2.3.6 - 2.3.7
PDF
PDF
PDF
Prml4.4 ラプラス近似~ベイズロジスティック回帰
PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4
PDF
PRML勉強会第3回 2章前半 2013/11/28
PDF
PPTX
パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半
PDF
PPTX
More Related Content
PDF
PDF
[PRML] パターン認識と機械学習(第2章:確率分布)
PDF
PDF
PDF
PPTX
PPTX
PDF
PRML上巻勉強会 at 東京大学 資料 第1章前半
What's hot
PDF
PRML ベイズロジスティック回帰 4.5 4.5.2
PDF
PPTX
PDF
PPTX
PDF
PDF
PPTX
多項式あてはめで眺めるベイズ推定�~今日からきみもベイジアン~�
PDF
PDF
DARM勉強会第3回 (missing data analysis)
PDF
PDF
PRML復々習レーン#2 2.3.6 - 2.3.7
PDF
PDF
PDF
Prml4.4 ラプラス近似~ベイズロジスティック回帰
PDF
2013.12.26 prml勉強会 線形回帰モデル3.2~3.4
PDF
PRML勉強会第3回 2章前半 2013/11/28
PDF
PPTX
パターン認識と機械学習(PRML)第2章 確率分布 2.3 ガウス分布
PDF
PRML上巻勉強会 at 東京大学 資料 第1章後半
Similar to パターン認識と機械学習 〜指数型分布族とノンパラメトリック〜
PDF
PPTX
PDF
[PRML] パターン認識と機械学習(第1章:序論)
PDF
PDF
PDF
Pattern Recognition and Machine Learning study session - パターン認識と機械学習 勉強会資料
PPTX
Bernoulli distribution and multinomial distribution (ベルヌーイ分布と多項分布)
PDF
Infomation geometry(overview)
PPTX
Introduction to Statistical Estimation (統計的推定入門)
PDF
Bishop prml 9.3_wk77_100408-1504
PDF
PDF
PDF
PRML輪講用資料10章(パターン認識と機械学習,近似推論法)
PDF
PPT
C:\D Drive\Prml\プレゼン\パターン認識と機械学習2 4章 D0703
PDF
PRML2.3.8~2.5 Slides in charge
PDF
PDF
PRML_titech 2.3.1 - 2.3.7
PDF
PDF
Nonparametric Factor Analysis with Beta Process Priors の式解説
パターン認識と機械学習 〜指数型分布族とノンパラメトリック〜 1. 2. 3. 目次
• 2.4 指数型分布族
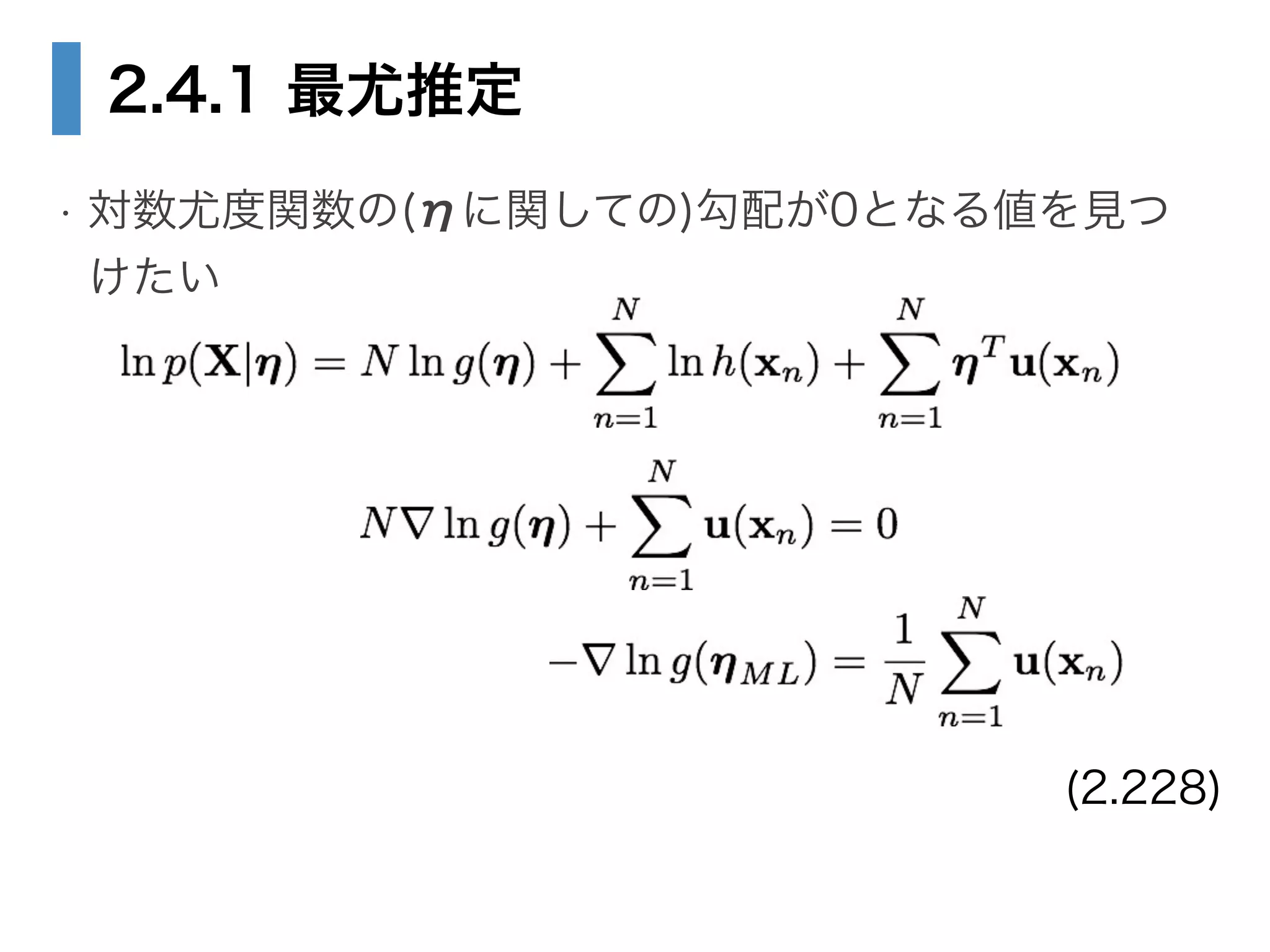
• 2.4.1 最尤推定と十分統計量
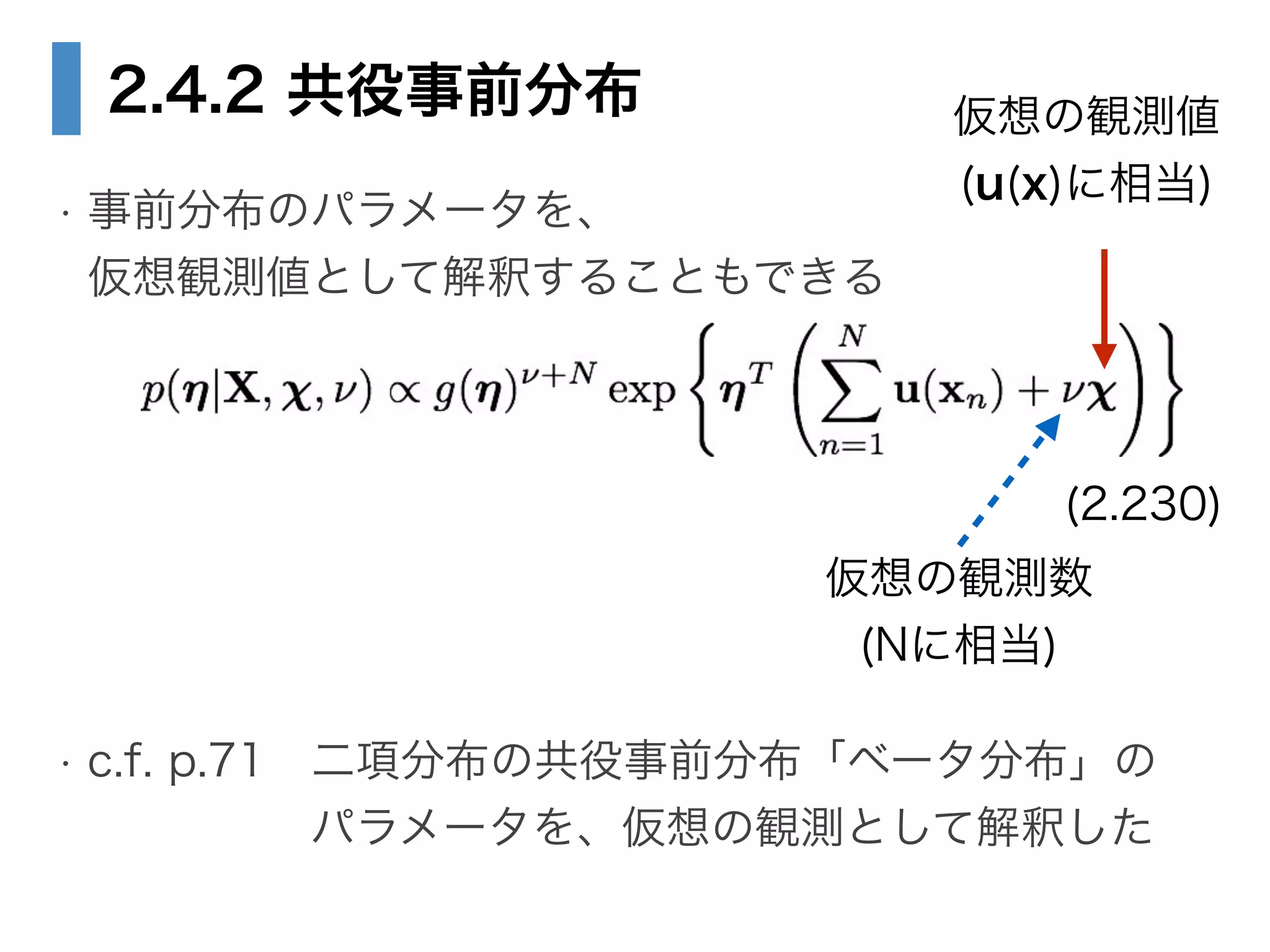
• 2.4.2 共役事前分布
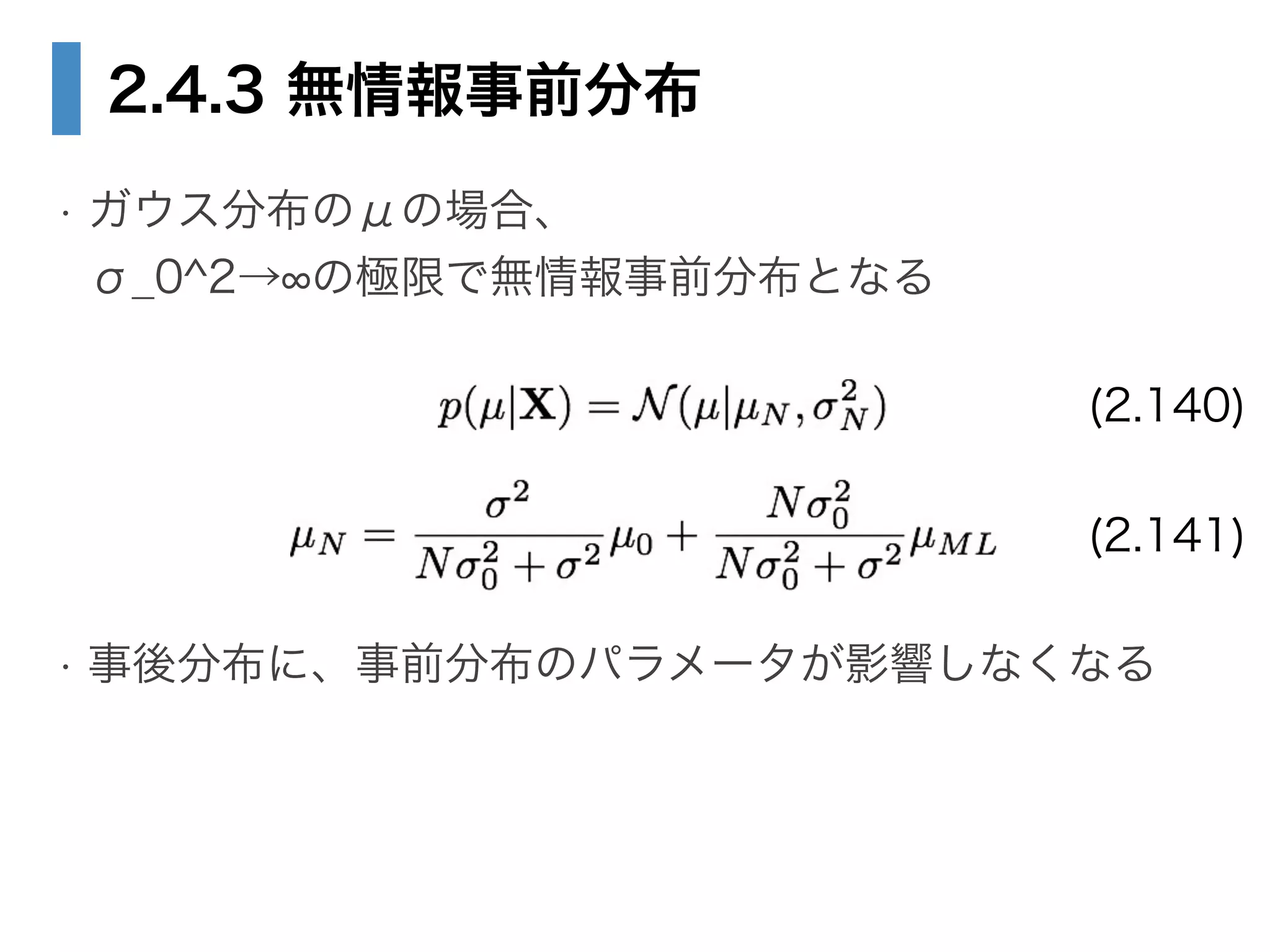
• 2.4.3 無情報事前分布
• 2.5 ノンパラメトリック法
• 2.5.1 カーネル密度推定法
• 2.5.2 最近傍法
4. 5. 6. 2.4 指数型分布族(p.110)
!
• : ηに関する関数
• 確率密度関数の積分値が1になるように
正規化するためのもの
(2.194)
g(⌘)
g (⌘)
Z
h (x) exp ⌘T
u (x) dx = 1 (2.195)
Z(⌘) =
1
g (⌘)
=
Z
h (x) exp ⌘T
u (x) dx
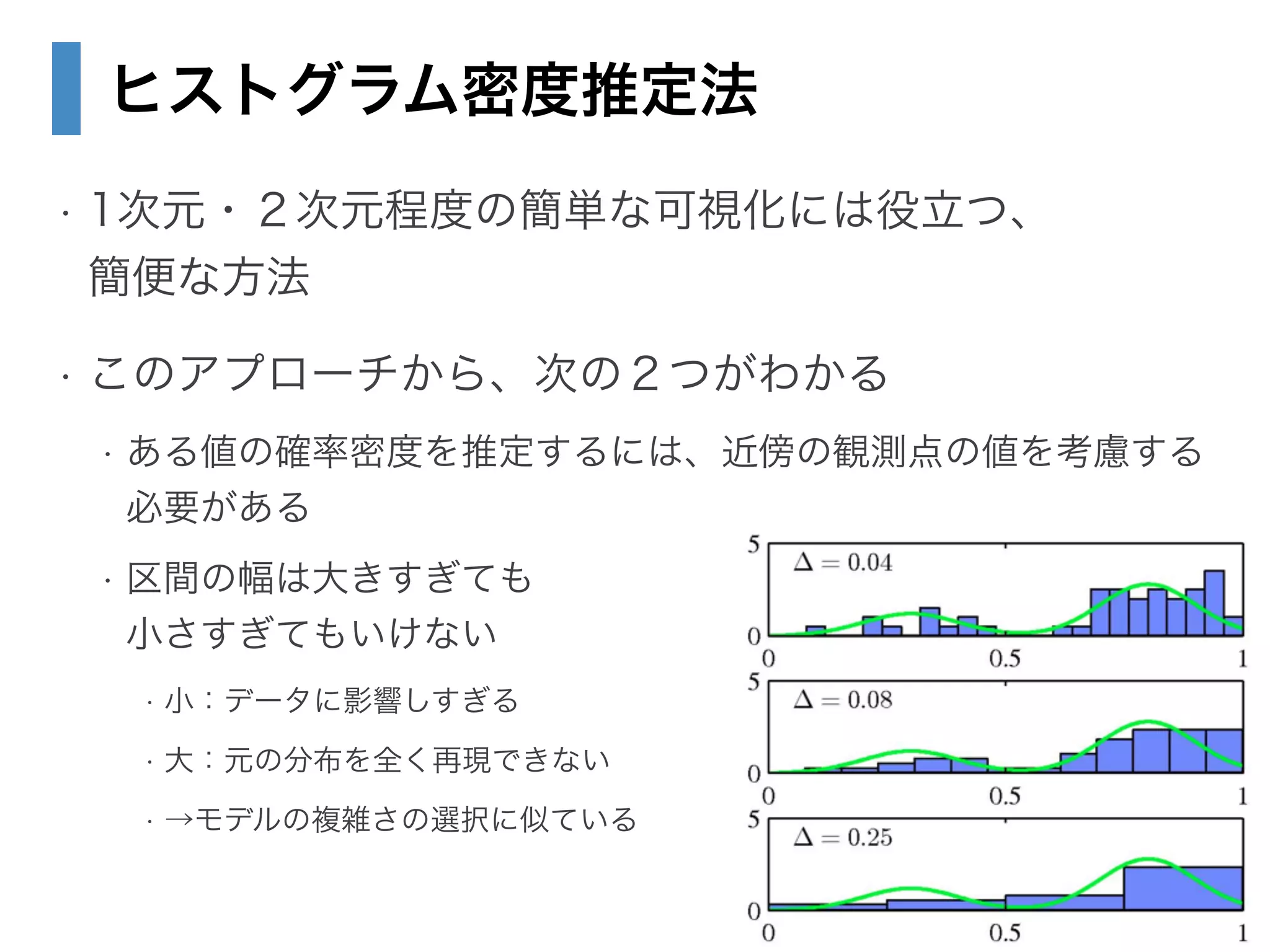
7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 2.5 ノンパラメトリック法
• パラメトリック
• 密度関数(モデル)を選んで、パラメータをデータから推定する
→ モデルがデータを表すのに貧弱だと、予測精度は悪い
• 例) ガウス分布をデータに当てはめて、μ・σ^2を推定した
→ データが多峰性だと、ガウス分布では捉えられない
• ノンパラメトリック
• 分布の形状に置く仮定が少ない
• 例)多峰性だとか単峰性などの仮定は置かない
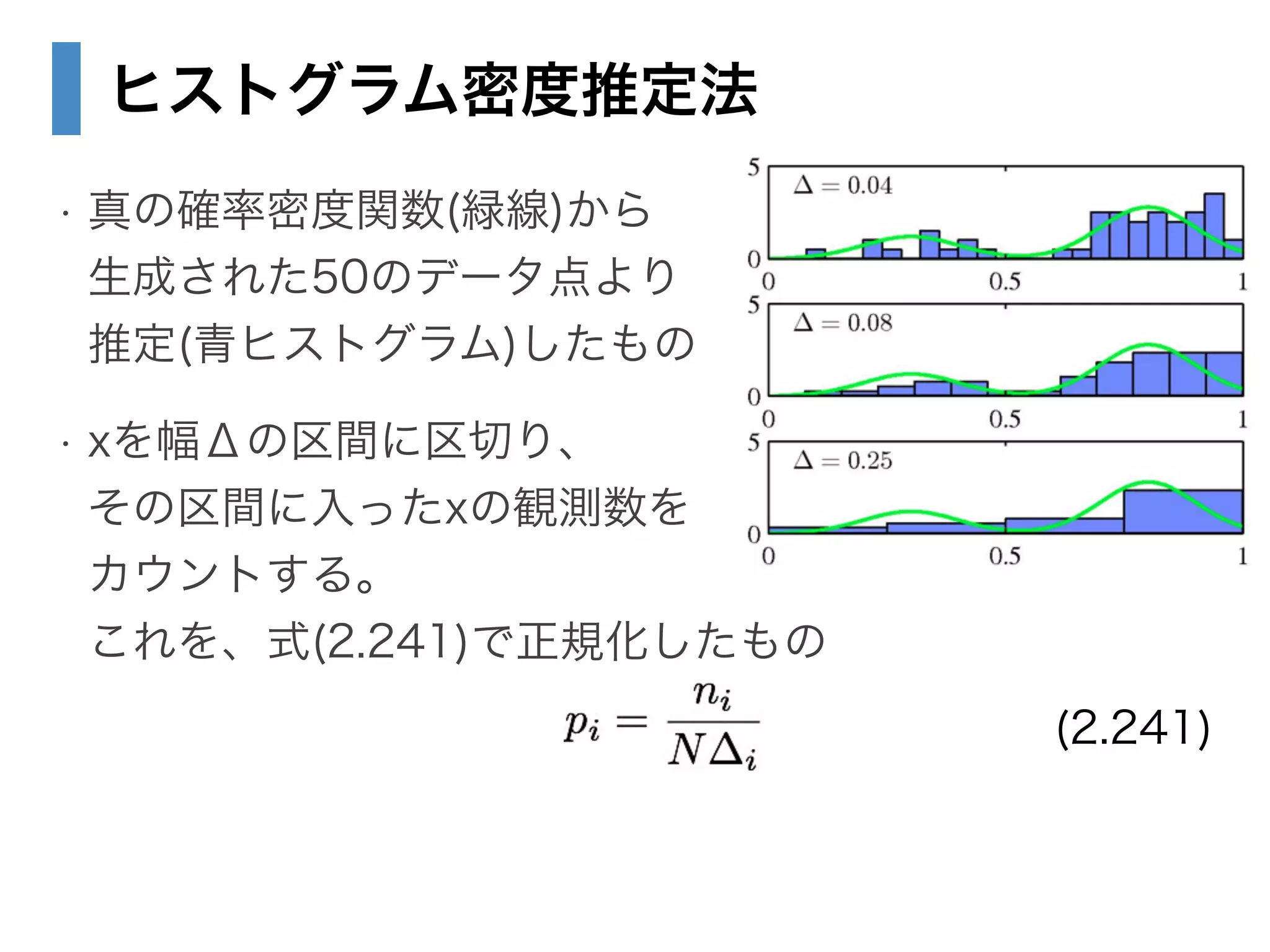
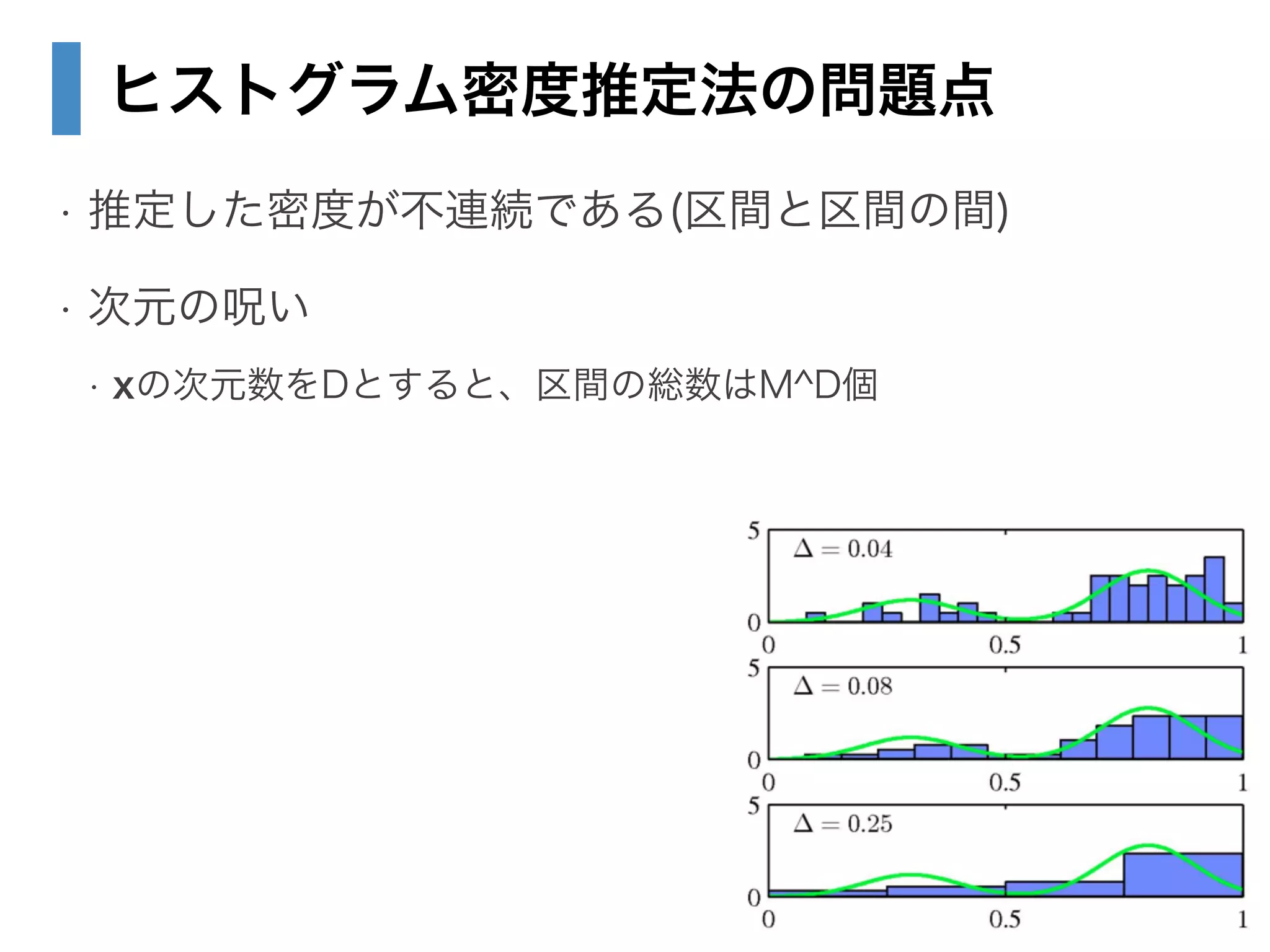
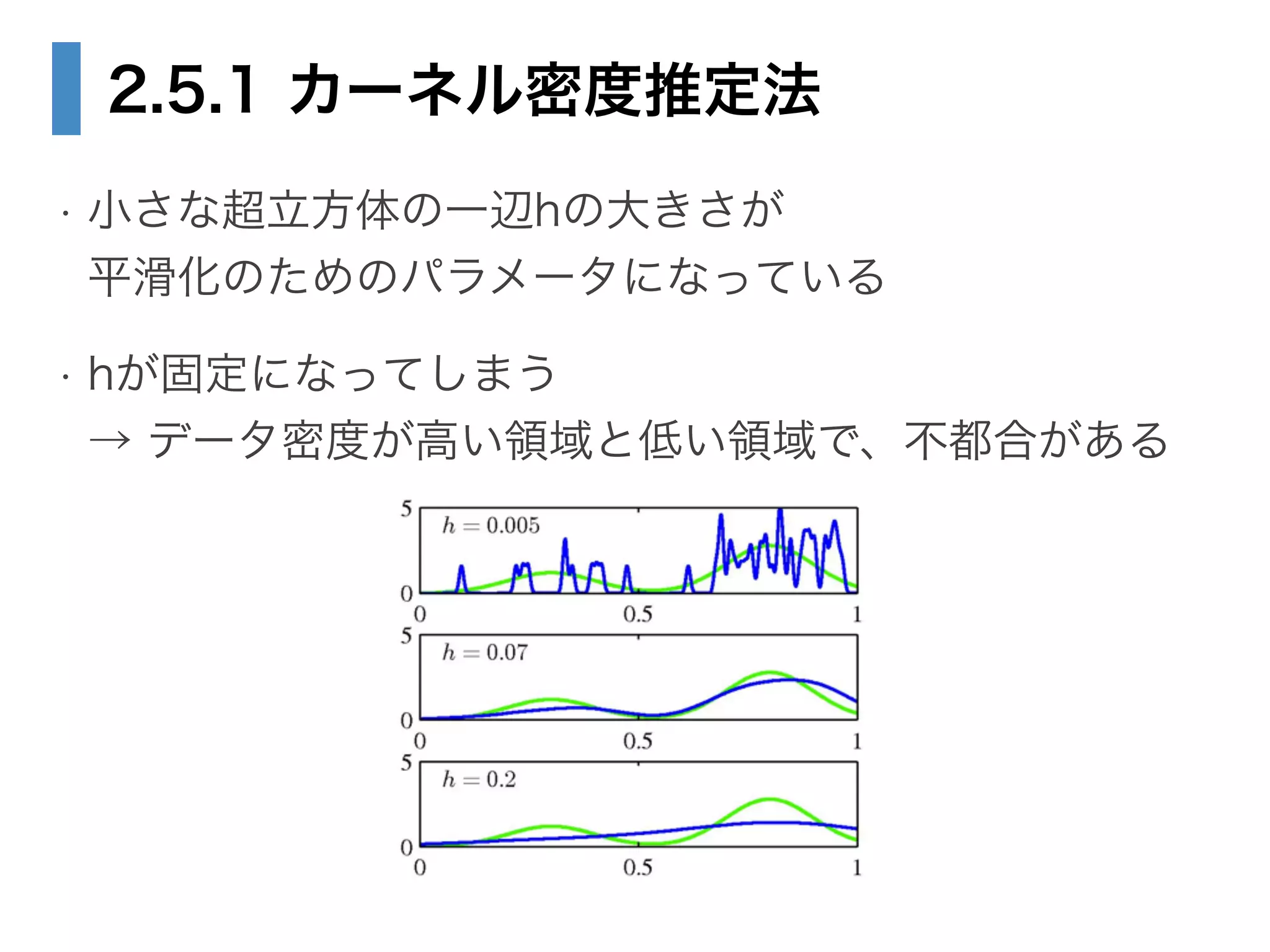
22. 23. 24. 25. 26. 27. 28. 2.5.1 カーネル密度推定法
• Vを固定し、Kを推定したい
• 確率密度p(x)を求めたい点をx、観測点をx_nとする
• 一辺がhで、xを中心とする小さな超立方体の
中にある点の総数は
!
• 一辺hの超立方体なので、Vはh^Dとなり、
K =
KX
n=1
k
✓
x xn
h
◆
p(x) =
1
N
KX
n=1
1
hD
k
✓
x xn
h
◆
(2.248)
(2.249)
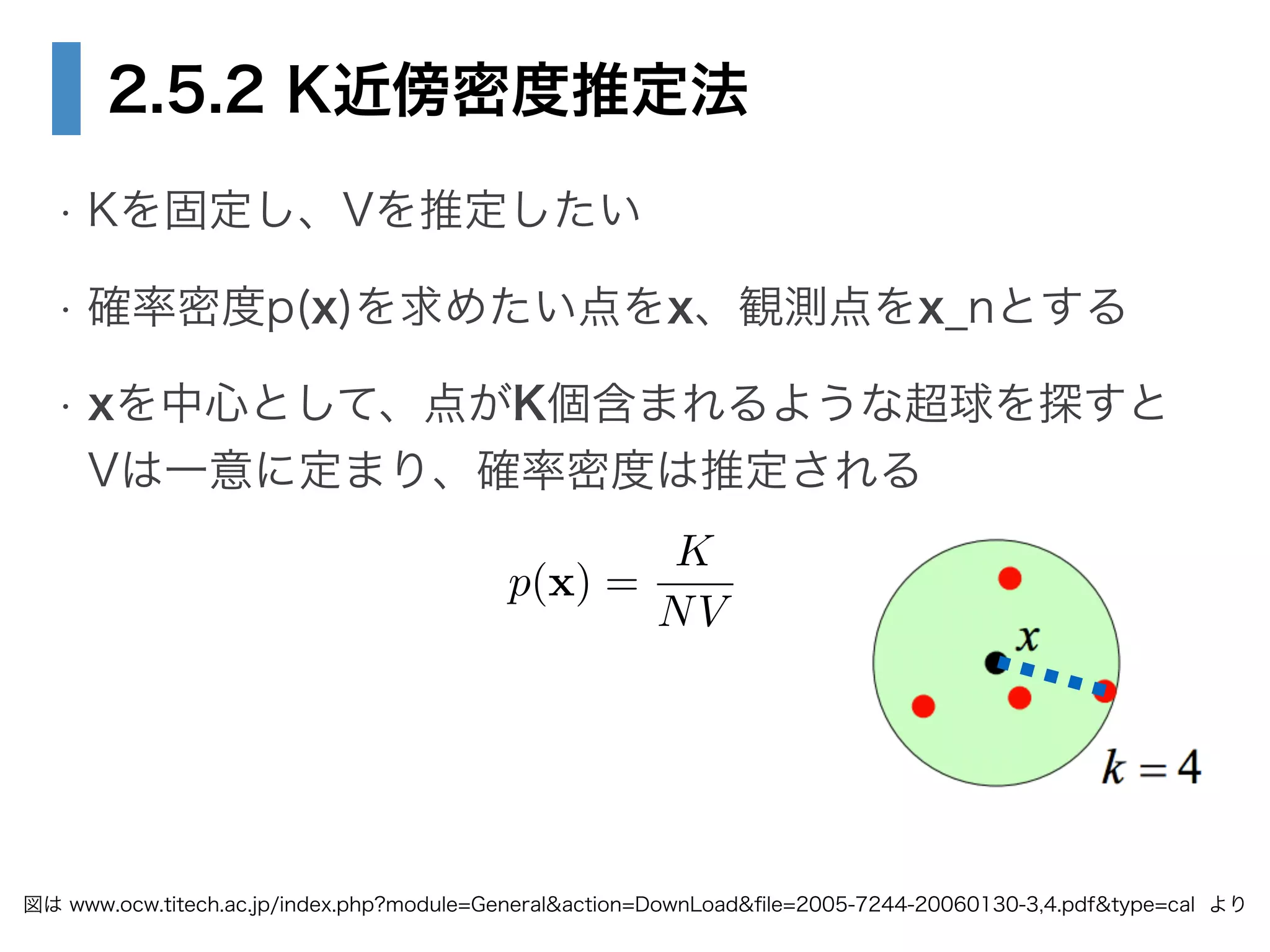
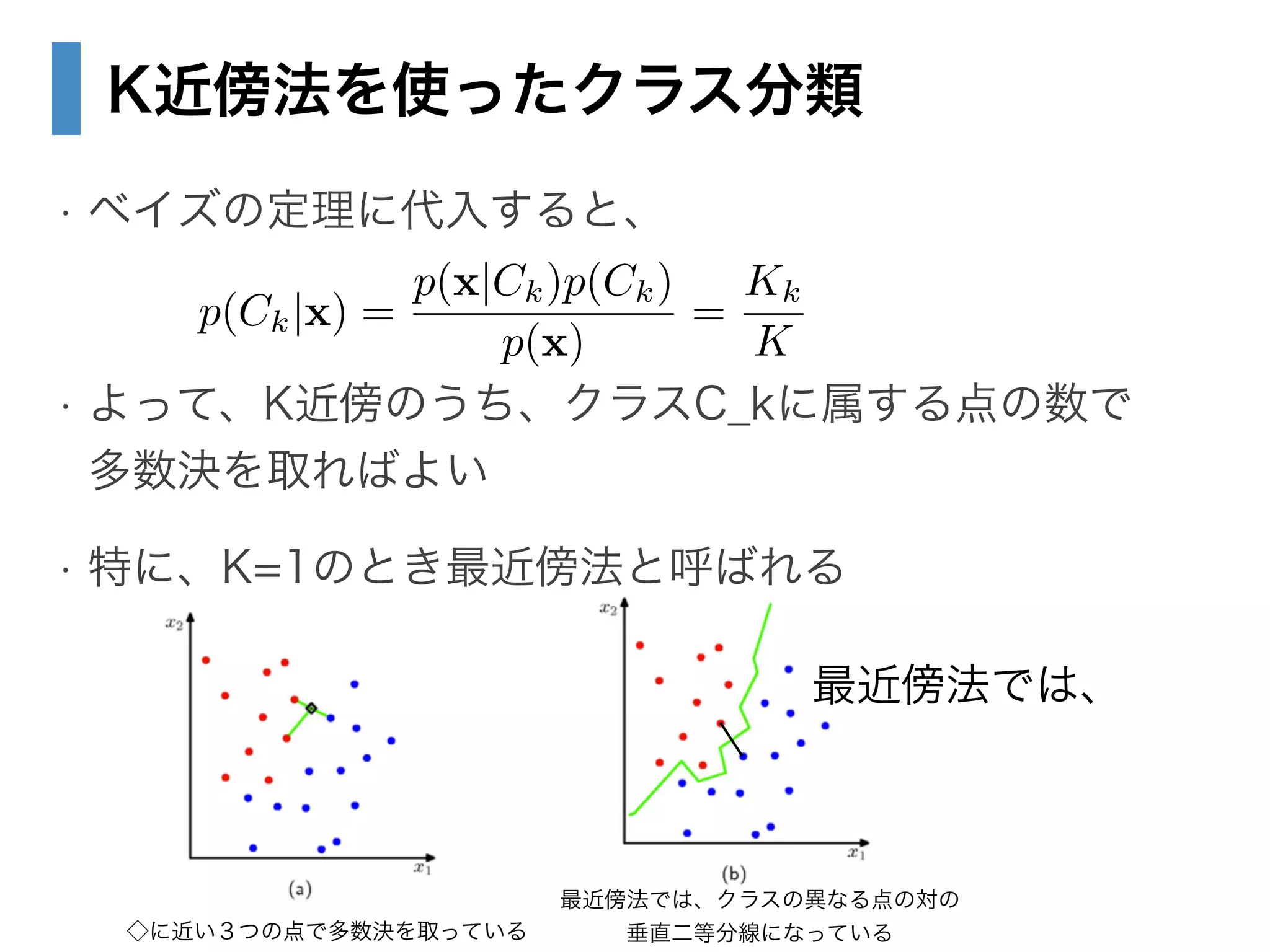
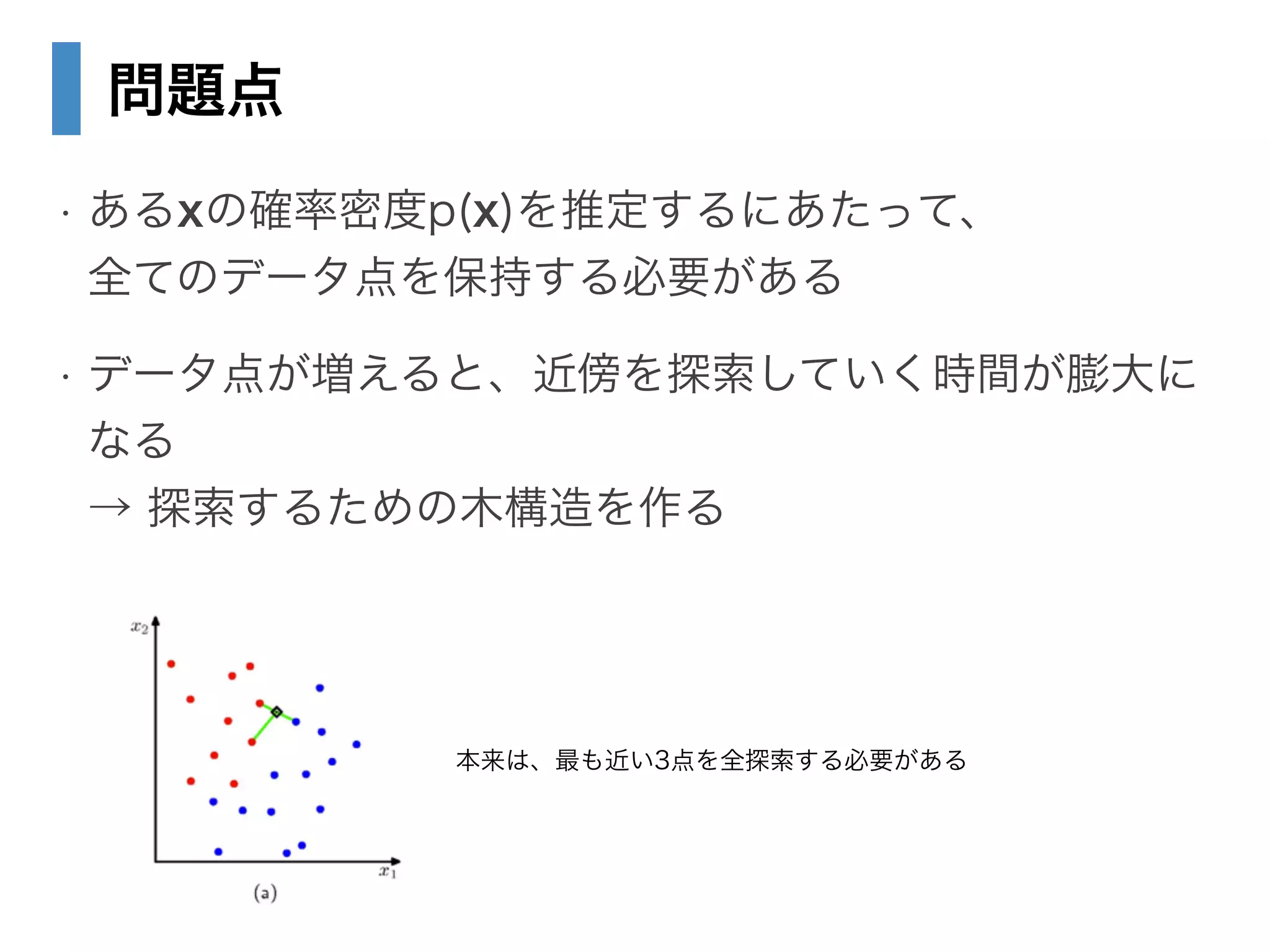
29. 30. 2.5.2 K近傍密度推定法
• Kを固定し、Vを推定したい
• 確率密度p(x)を求めたい点をx、観測点をx_nとする
• xを中心として、点がK個含まれるような超球を探すと
Vは一意に定まり、確率密度は推定される
図は www.ocw.titech.ac.jp/index.php?module=General&action=DownLoad&file=2005-7244-20060130-3,4.pdf&type=cal より
p(x) =
K
NV
31. 32. 33. 34. 35. 36. 37.