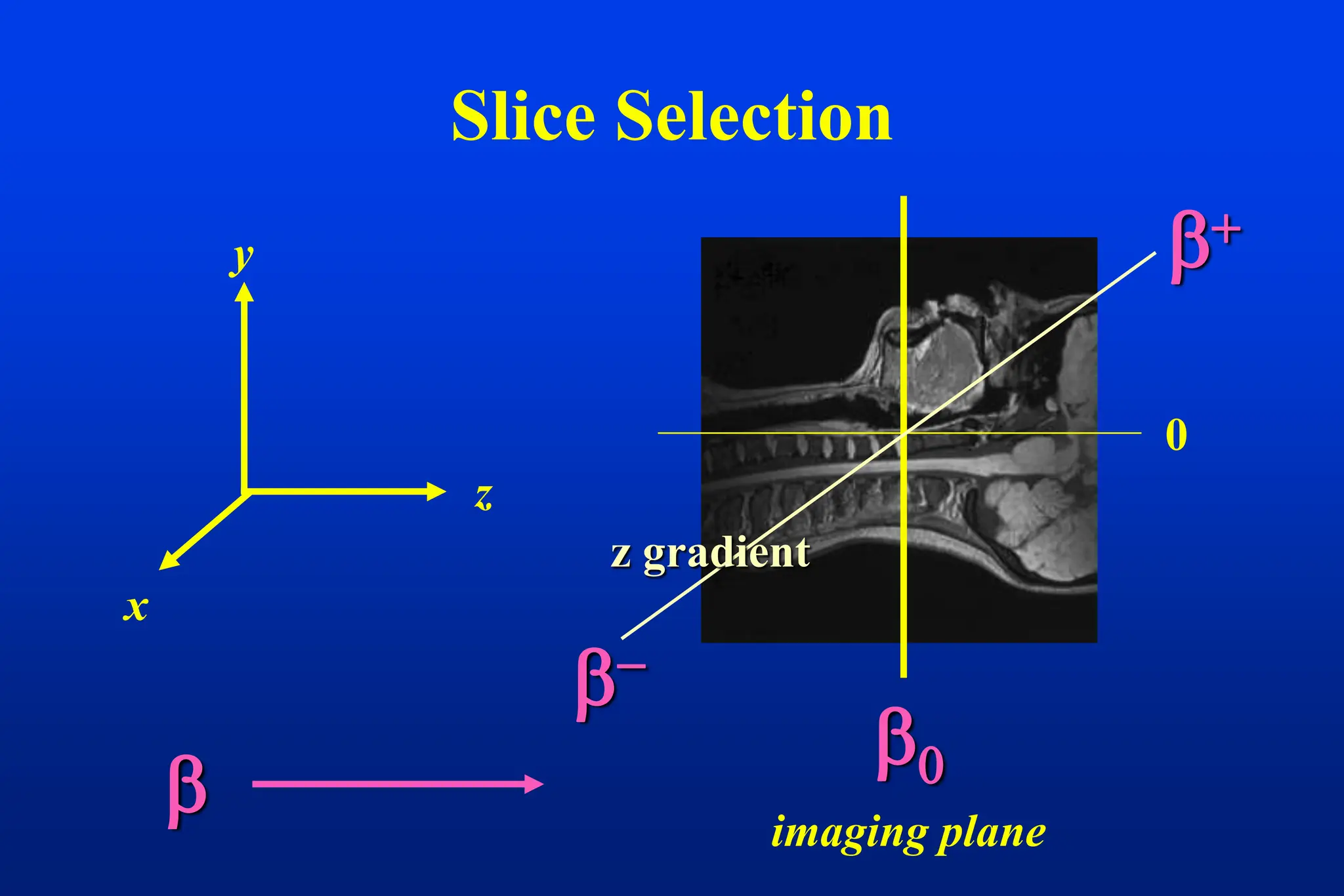
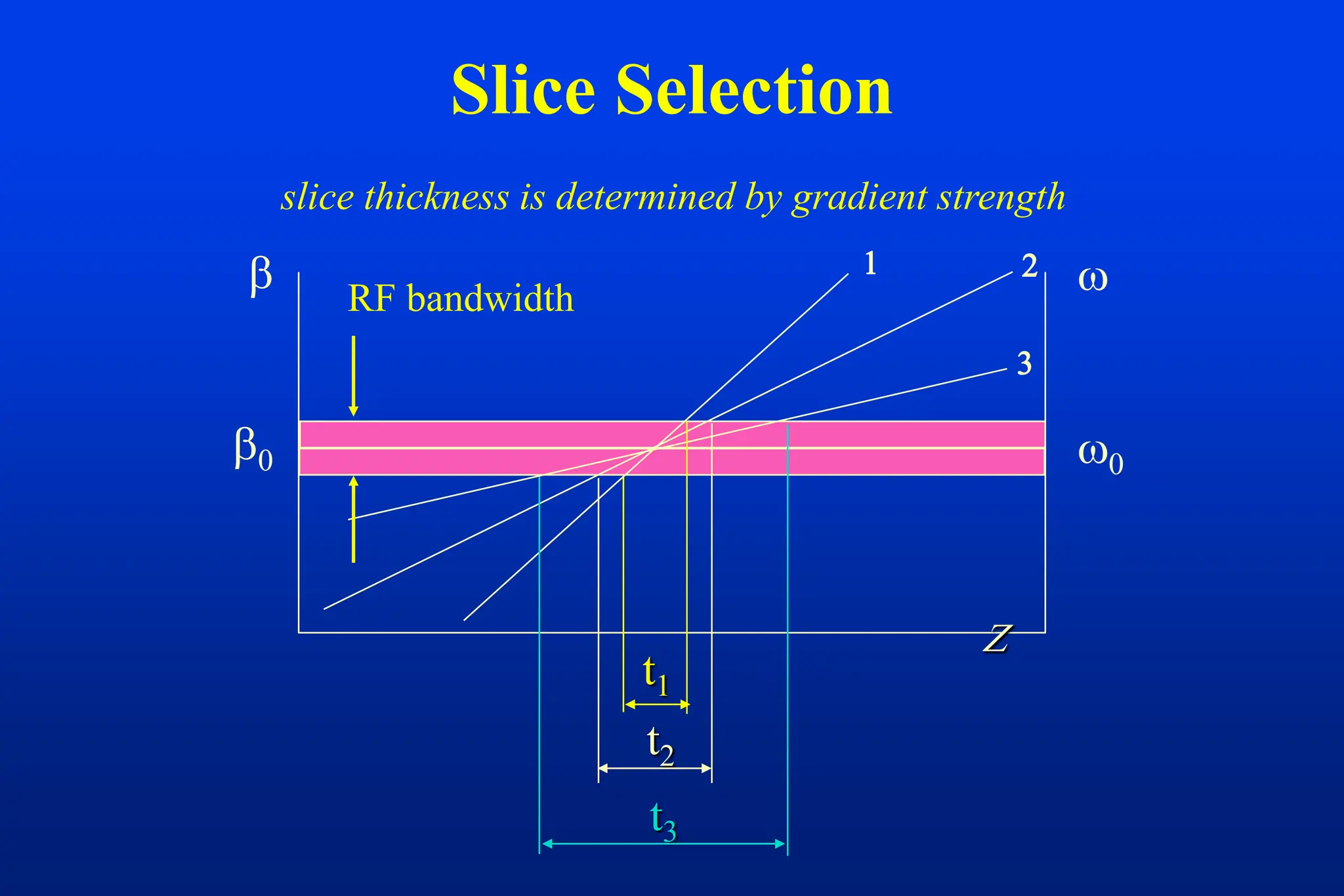
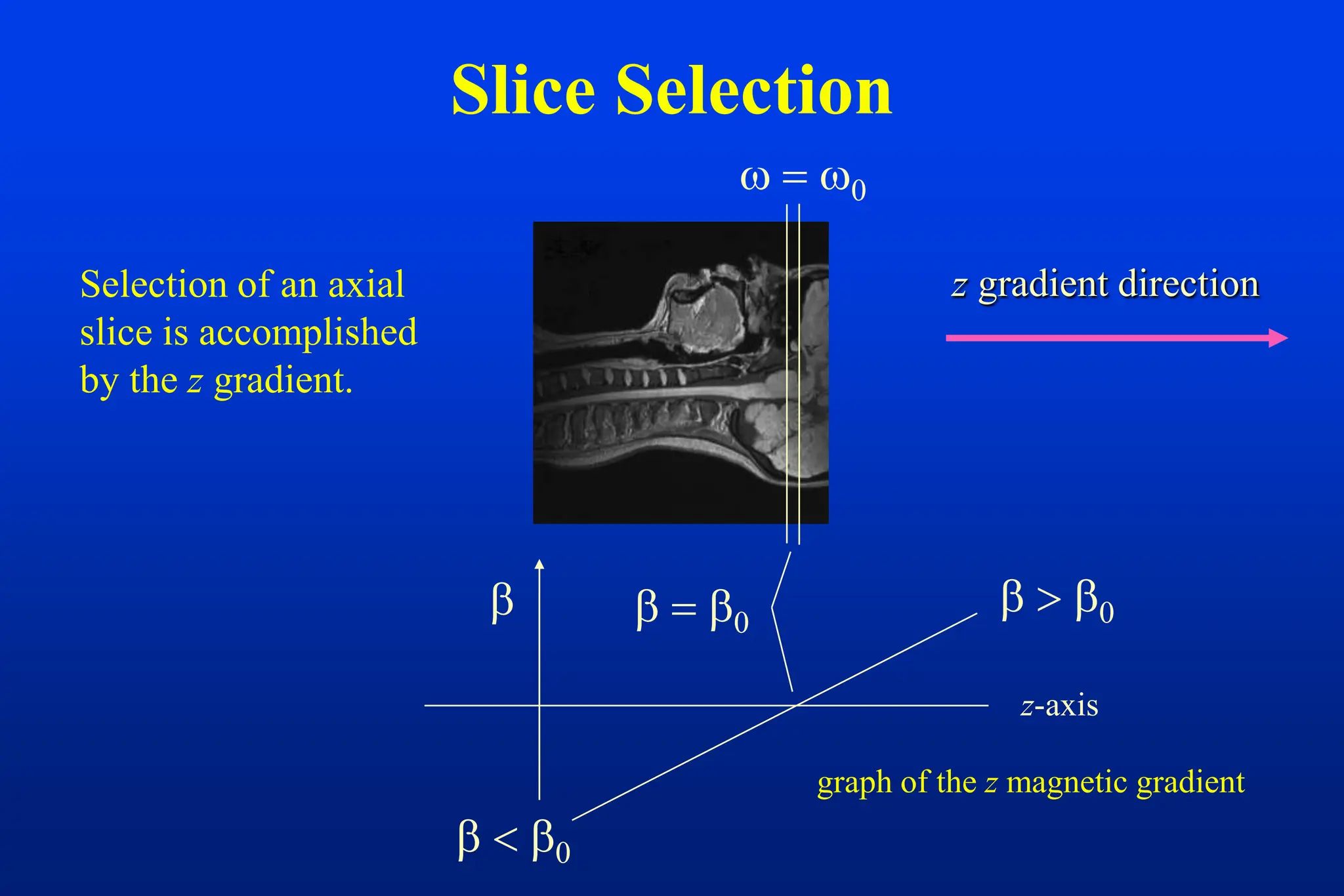
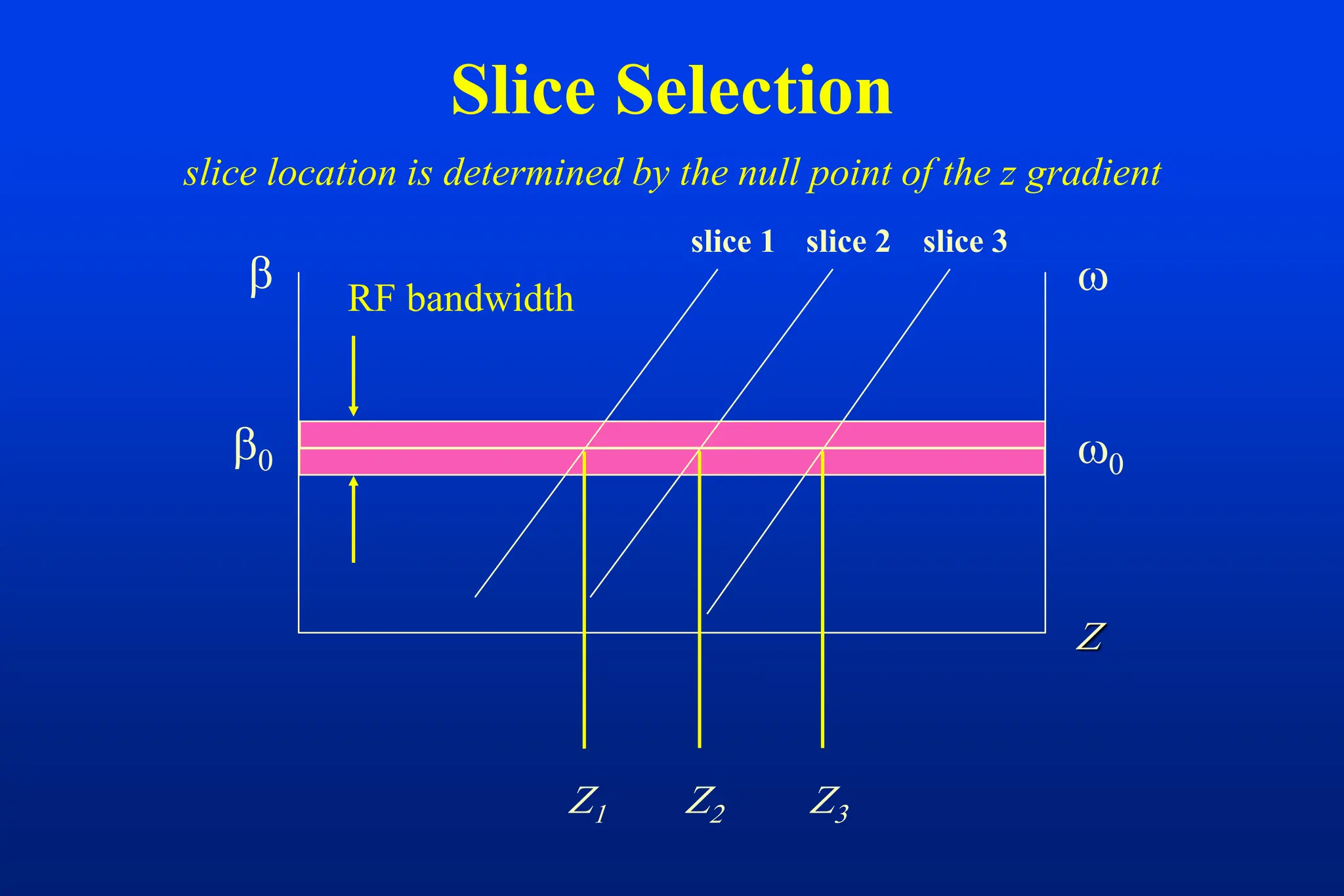
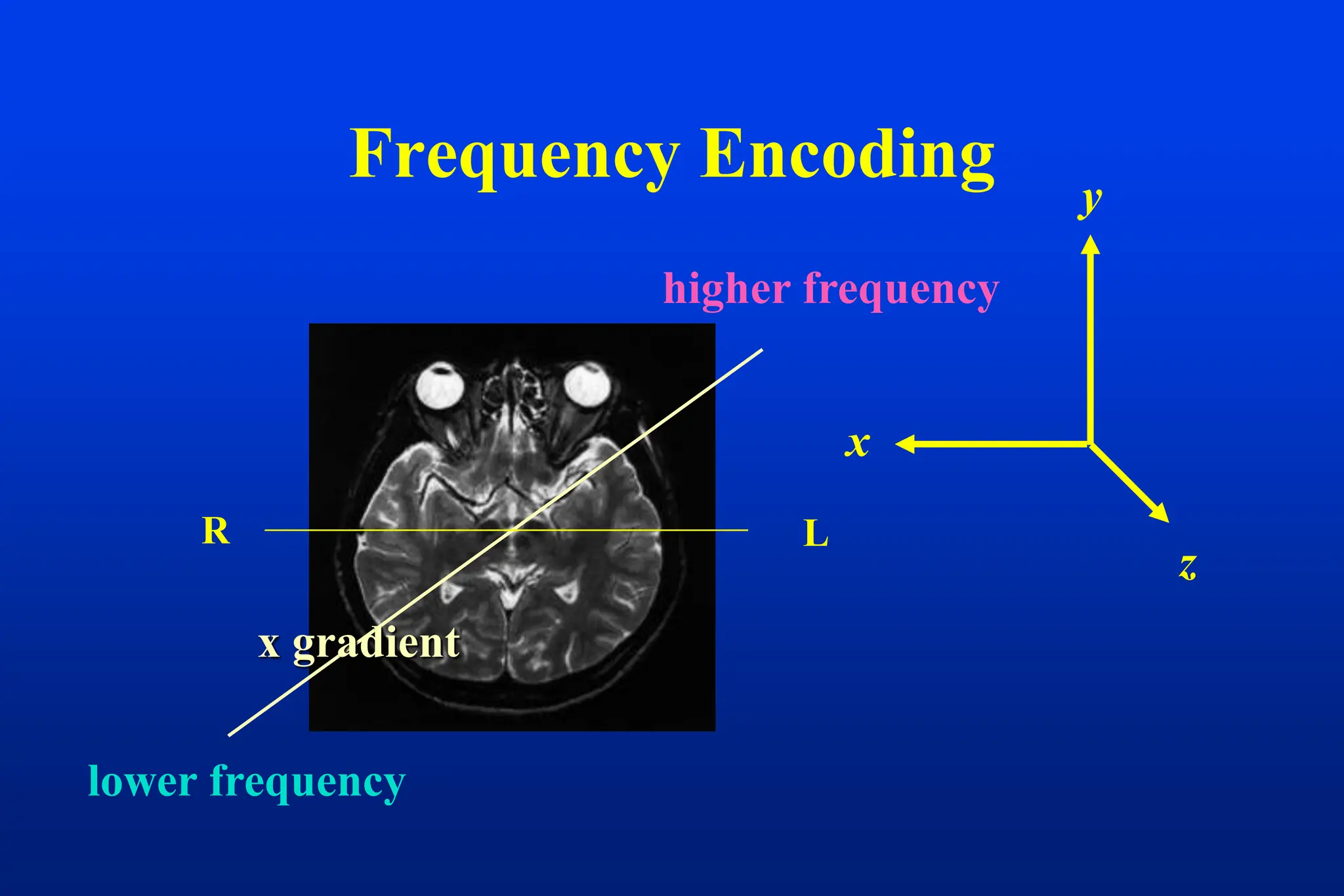
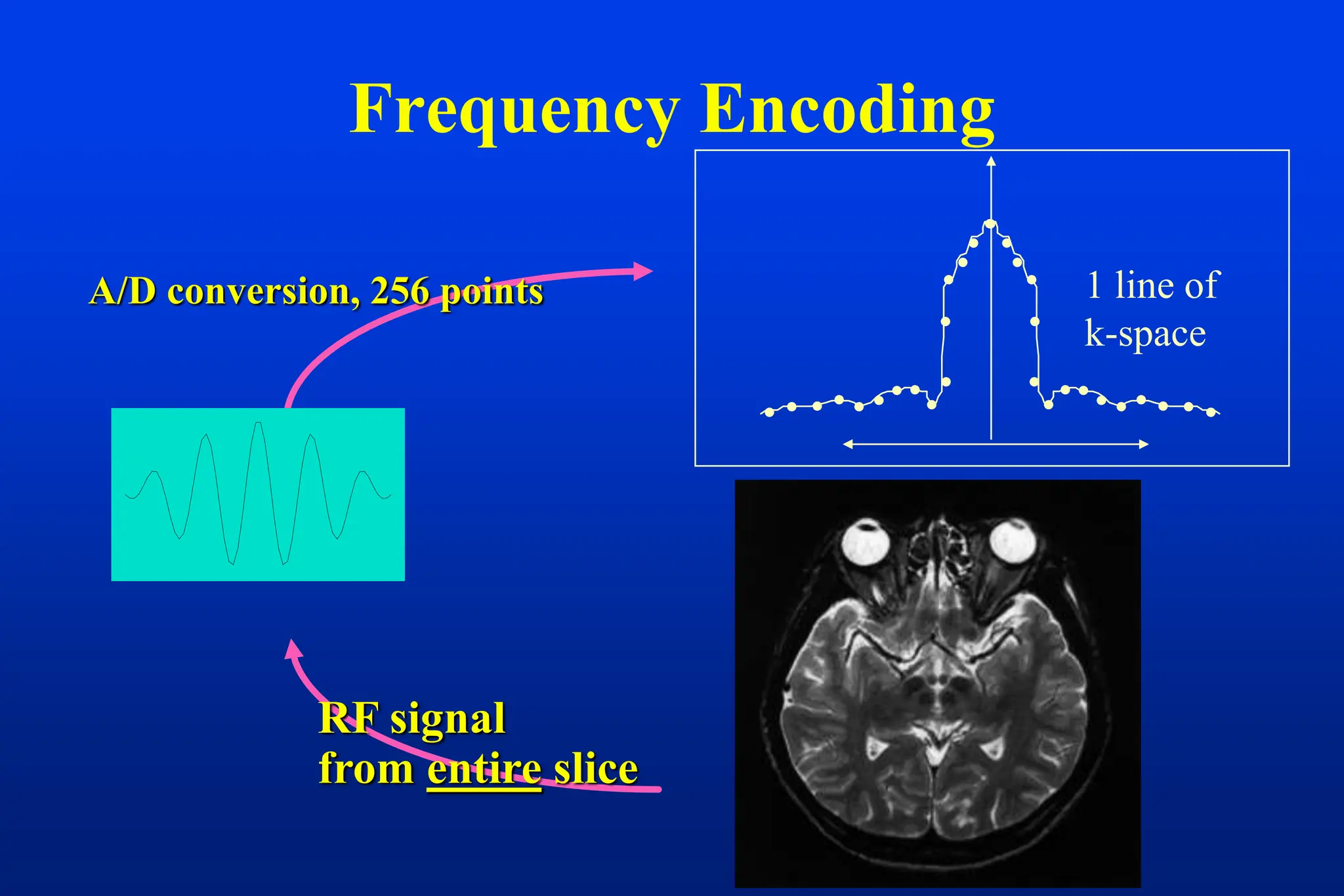
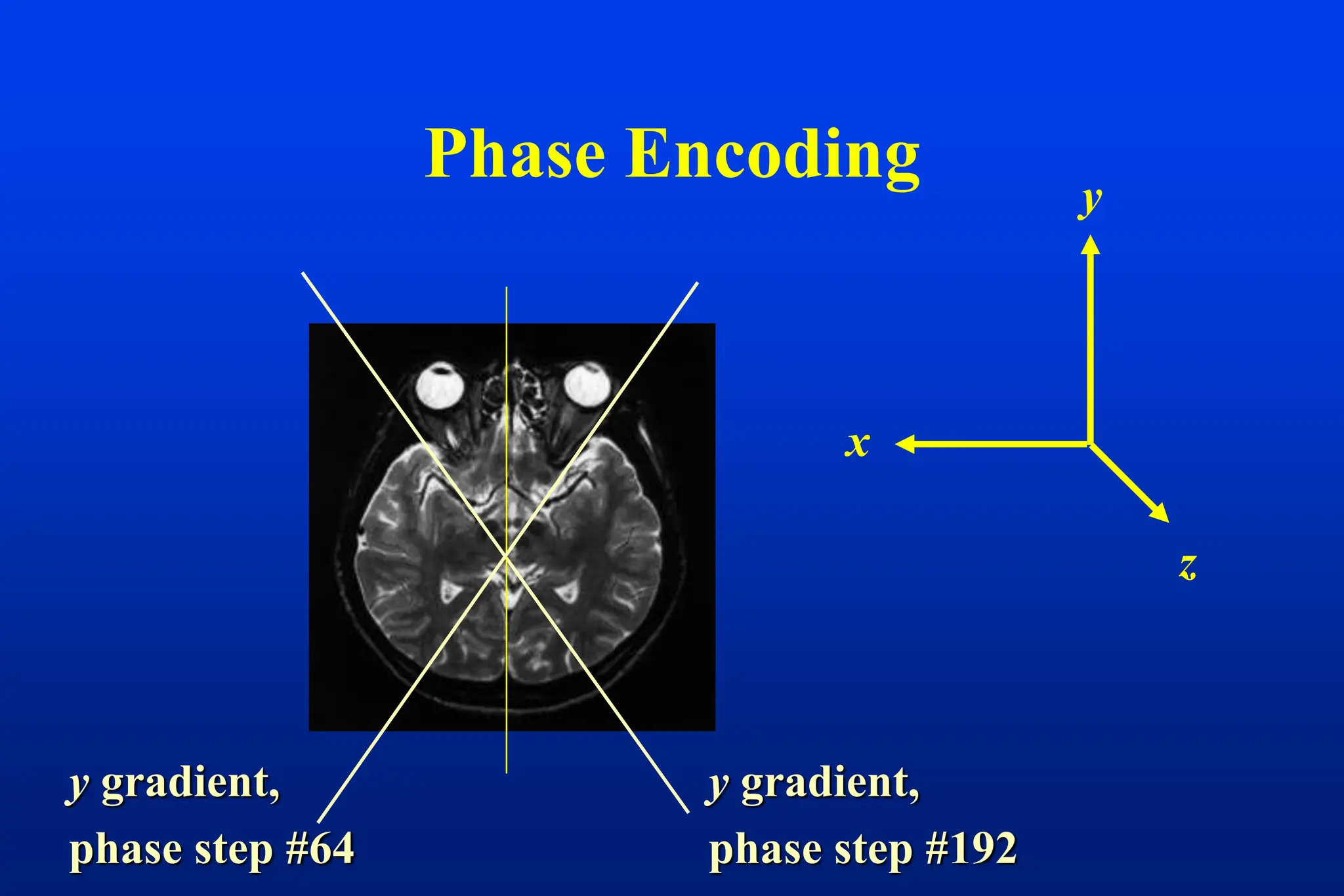
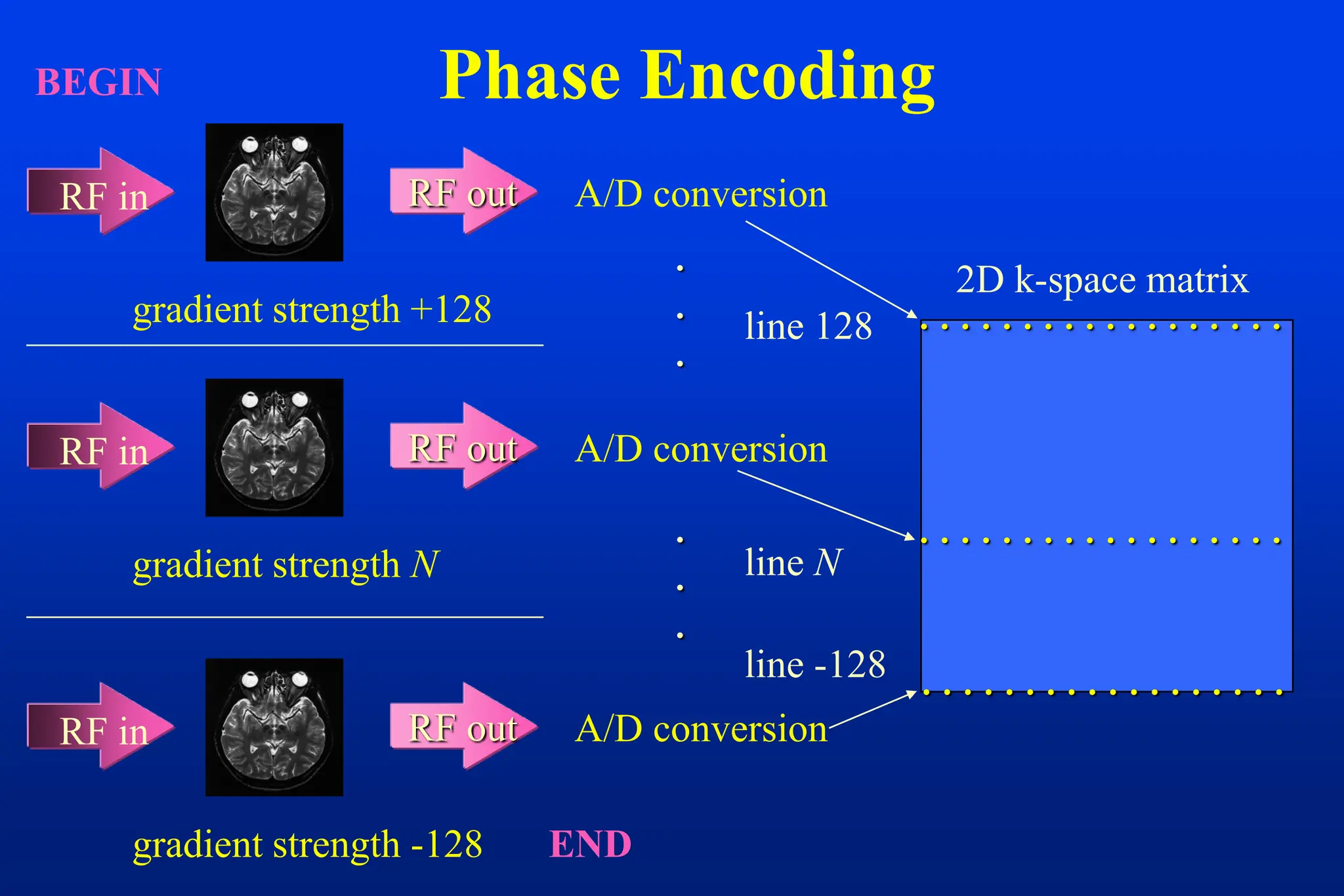
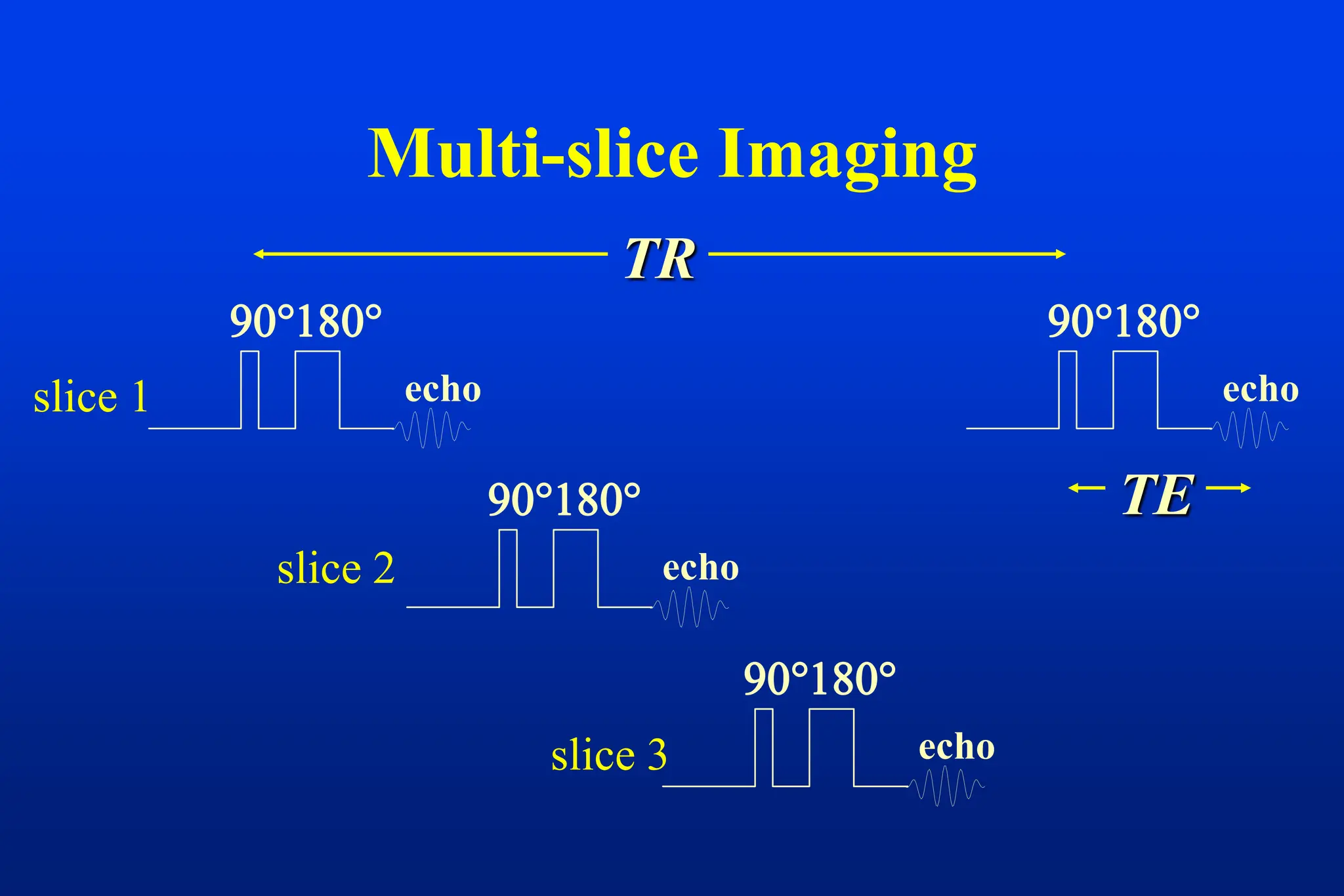
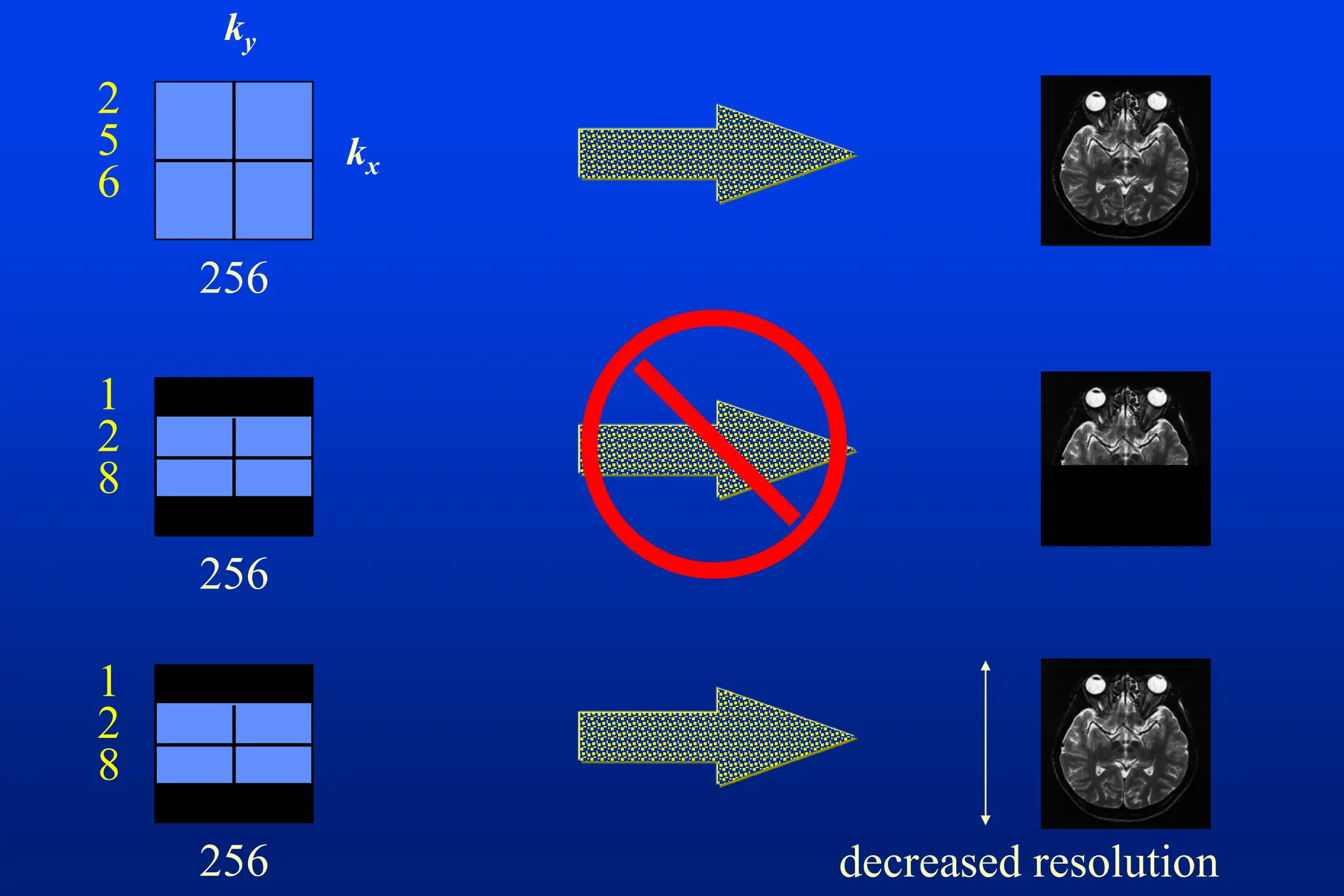
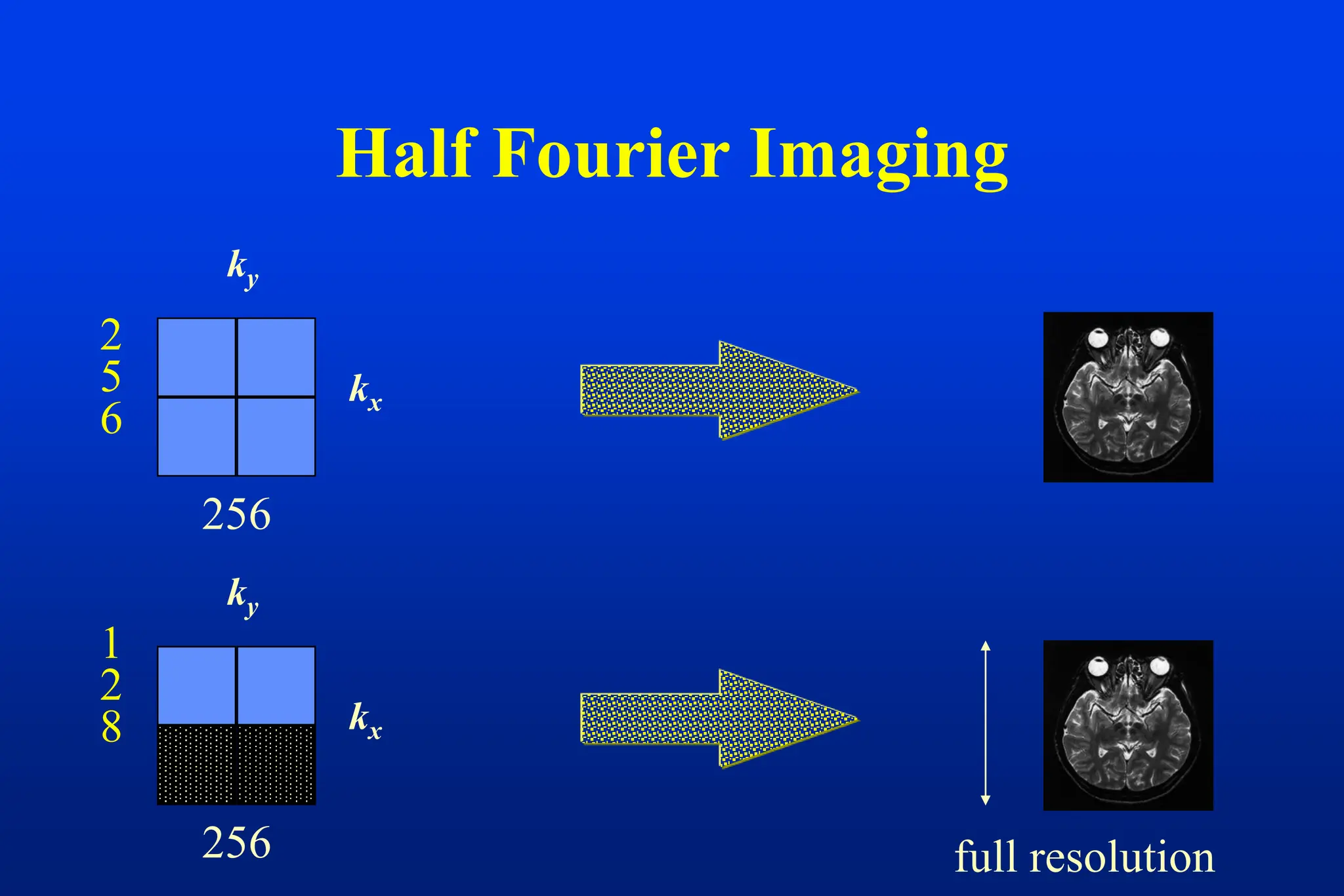
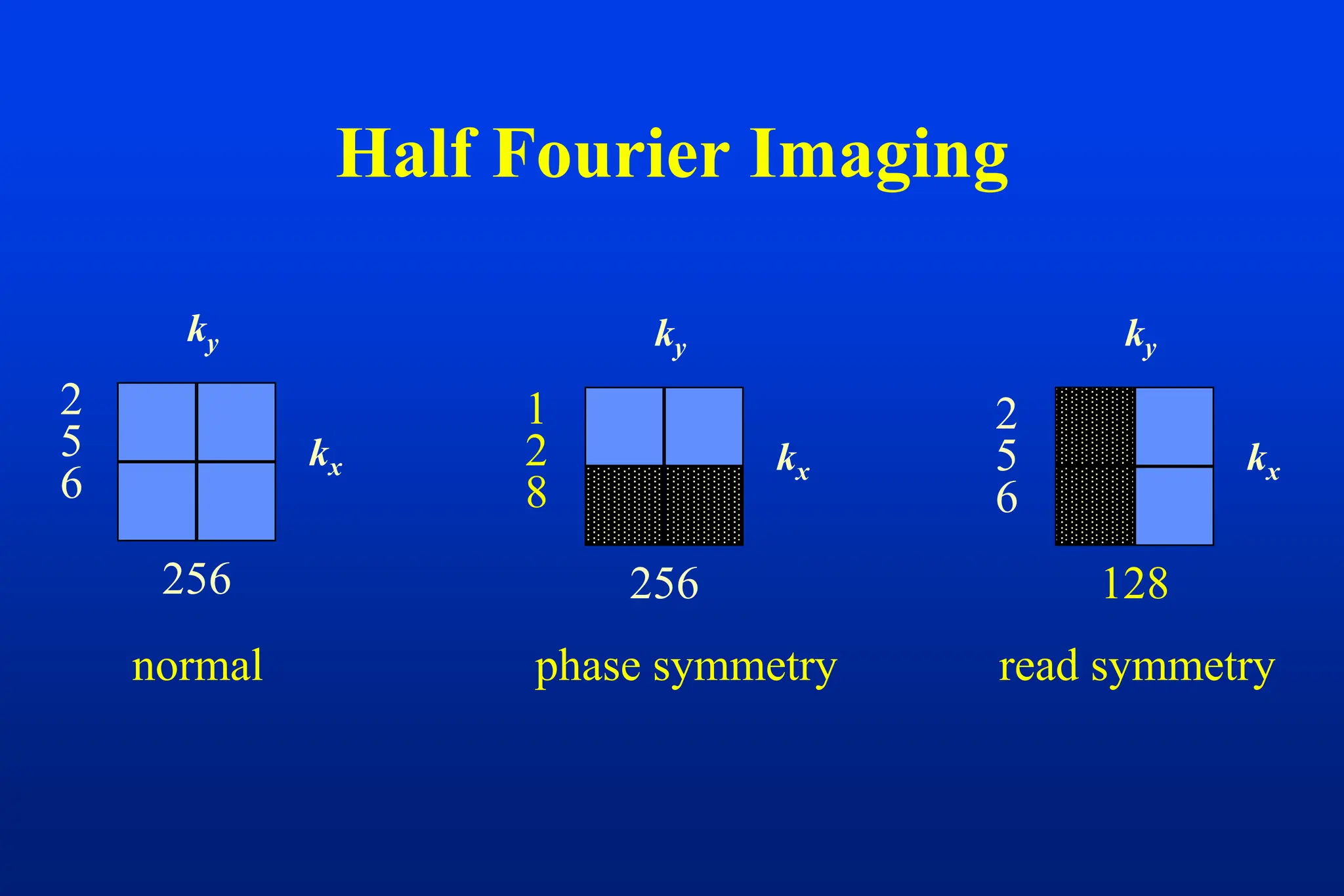
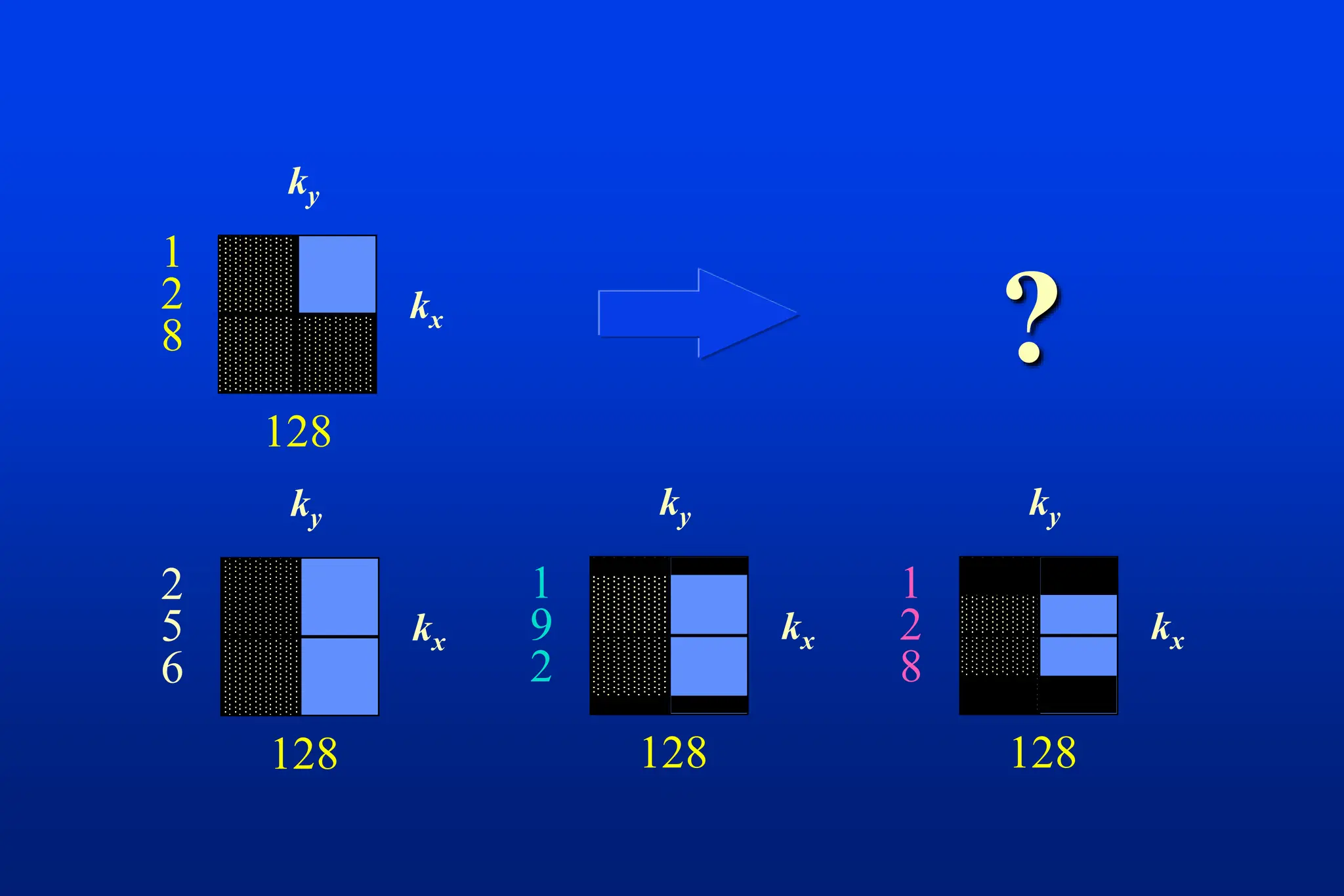
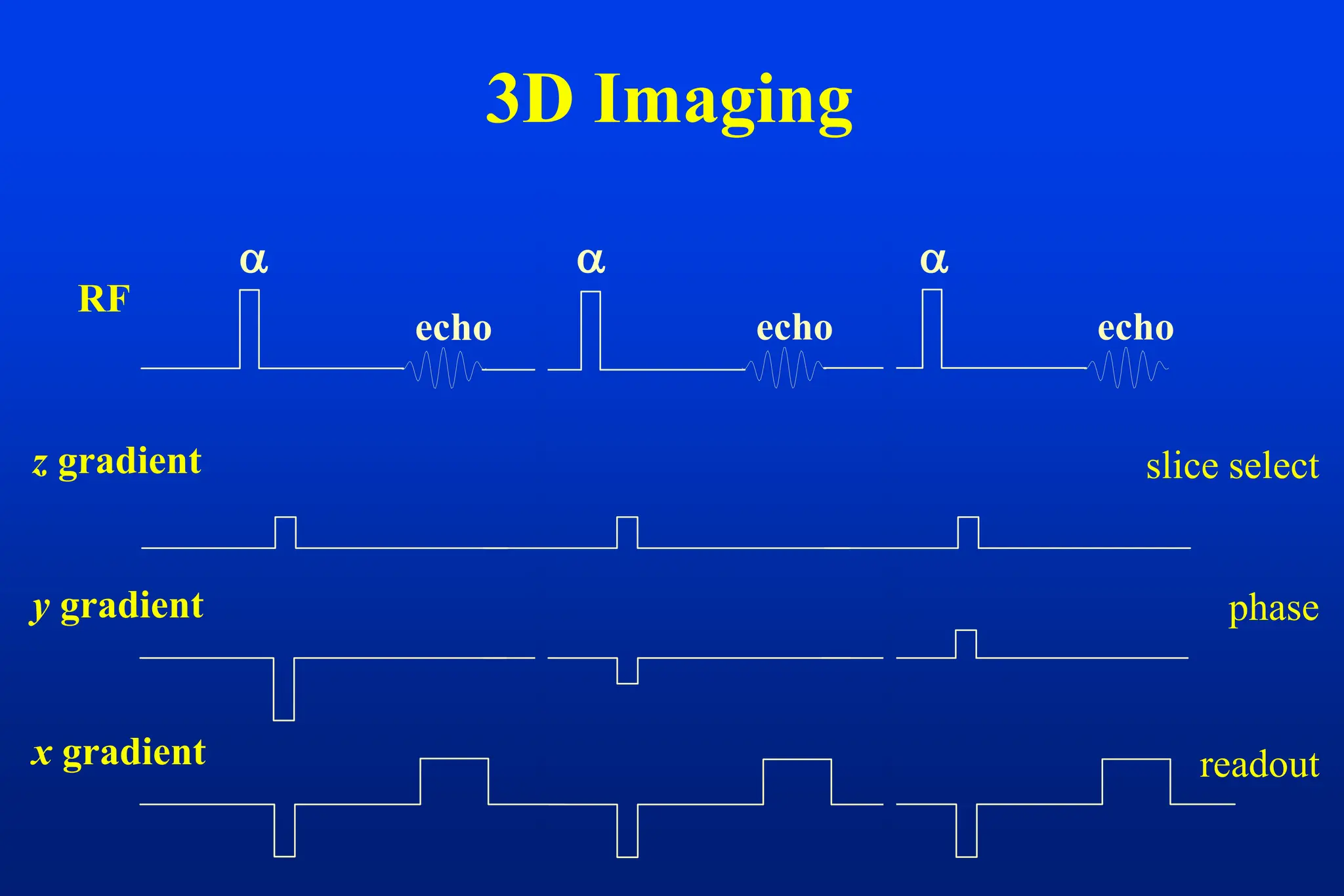
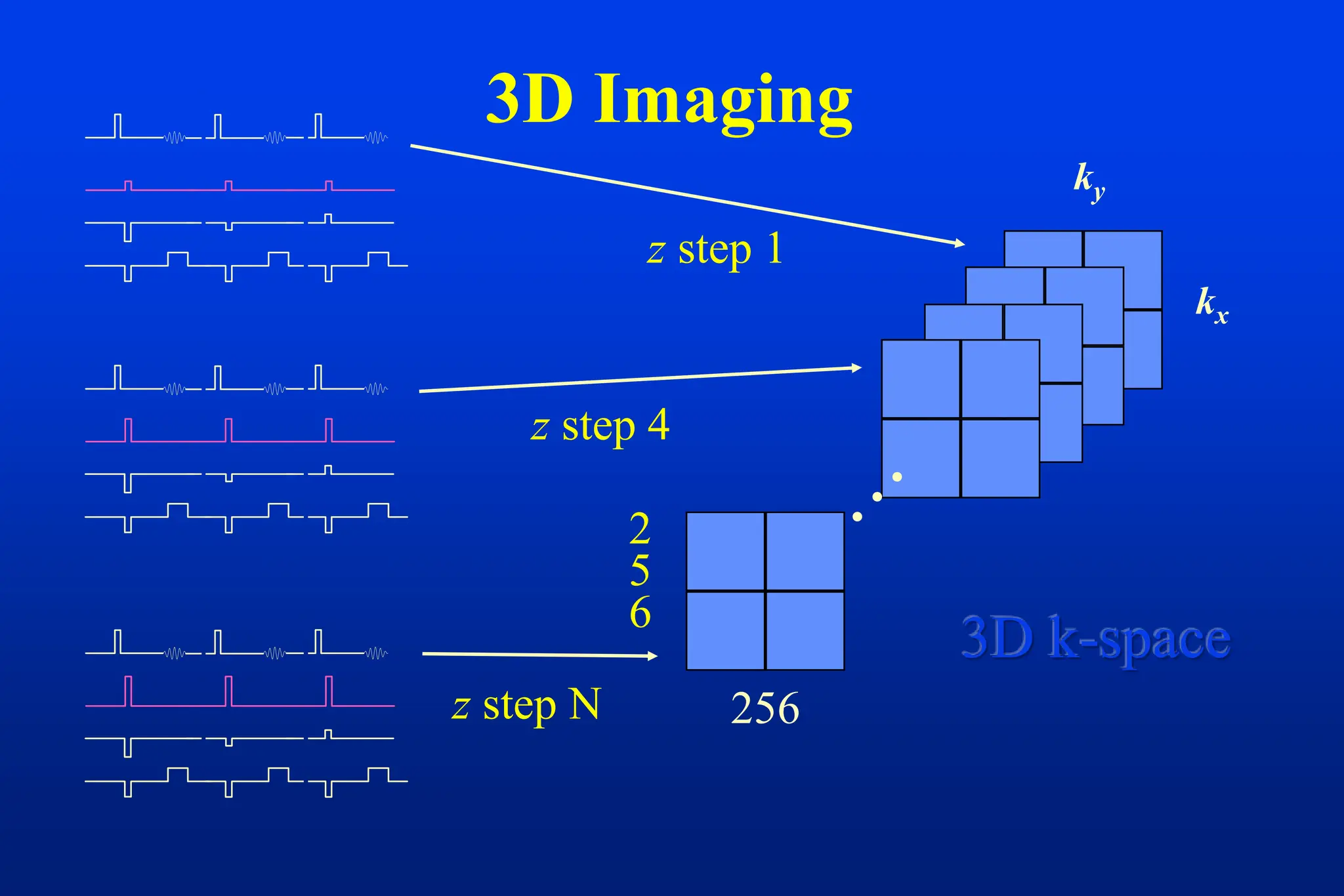
This document discusses techniques for spatial encoding in MRI. Slice selection is performed using a gradient in the z-direction. Within the slice, frequency encoding uses a left-right gradient, while phase encoding with a head-foot gradient fills the remaining direction of k-space. Multiple slices can be acquired simultaneously using interleaved acquisition between RF pulses. Resolution can be reduced and speed increased using half Fourier and parallel imaging techniques. Three-dimensional imaging excites the entire volume and uses two phase encoding gradients.

1. Topics
• spatial encoding - part 2

2. Slice Selection

z
y
x
0
imaging plane



z gradient

3. Slice Selection
slice thickness is determined by gradient strength




RF bandwidth




t1
t2
t3

4. Slice Selection
Selection of an axial
slice is accomplished
by the z gradient.
z gradient direction

graph of the z magnetic gradient
z-axis
 



5. Slice Selection
slice location is determined by the null point of the z gradient




RF bandwidth
slice 1

slice 2 slice 3
  

6. Frequency Encoding
• Within the imaging plane, a small gradient is
applied left to right to allow for spatial
encoding in the x direction.
• Tissues on the left will have a slightly higher
resonance frequency than tissues on the right.
• The superposition of an x gradient on the
patient is called frequency encoding.
• Frequency encoding enables spatial localization
in the L-R direction only.

7. Frequency Encoding
z
y
x
x gradient
higher frequency
lower frequency
L
R

8. Frequency Encoding
RF signal
from entire slice
A/D conversion, 256 points 1 line of
k-space

9. Phase Encoding
• An additional gradient is applied in the
y direction to encode the image in the
remaining direction.
• Because the x gradient alters the
frequencies in the received signal according
to spatial location, the y gradient must alter
the phase of the signal.
• Thus, the points of k-space are revealed by
recording the digitized RF signal after a
phase encoding gradient application.

10. Phase Encoding
• The technique of phase encoding the second
dimension in the imaging plane is
sometimes referred to as spin warping.
• The phase encoding gradient is “stepped”
during the acquisition of image data for a
single slice. Each step provides a unique
phase encoding.
• For a 256 x 256 square image matrix, 256
unique phase encodings must be performed
for each image slice. The second 256 points
in the x direction are obtained by A to D
conversion of the received signal.

11. Phase Encoding
z
y
x
y gradient,
phase step #192
y gradient,
phase step #64

12. Phase Encoding
2D k-space matrix
gradient strength +128
RF in RF out A/D conversion
gradient strength N
RF in RF out A/D conversion
gradient strength -128
RF in RF out A/D conversion
                 






END
BEGIN
line 128
line N
line -128
                 
                 

13. Spin Echo Imaging
RF
z gradient
echo

echo

echo

y gradient
x gradient
slice select
phase
readout

14. Spin Echo Imaging
view -128
view -55
view 40
                 
                 
                 
k-space
256 x 256 points
row 40
row -55
row -128
A/D, 256 points
kx = frequency
ky = phase

15. • Acquisition of spatially encoded data as
described allows for reconstruction of the
MR image.
• The frequency and phase data are acquired
and form points in a 2D array .
• Reconstruction of the image is provided by
2D inverse Fourier transform of the
2D array.
• This method of spatially encoding the MR
image is called 2D FT imaging.
MR Image Reconstruction

16. Discrete Fourier Transform
F(kx,ky) is the 2D discrete Fourier transform of the
image f(x,y)
f x y
N
F k k e
xk yk
k
k
x y
j
N
x j
N
y
N
N
y
x
( , ) ( , )














1
2
2 2
0
1
0
1  
x
y
f(x,y)
kx
ky

k-space
F(kx,ky)
MR image

17. Image Resolution and Phase Encoding
• Resolution is always maximum in the
frequency encoding direction because the MR
signal is always digitized into 256 points.
• Resolution can vary in the phase encoding
direction depending on the number of phase
steps used to acquire the image.
• Because each phase encoding requires a
separate 90 and 180 degree pulse, image
acquisition time is proportional to the number
of phase encode steps.

18. Image Acquisition Time
 
TR number phase encodings NEX
msec 
60,000

19. • Example, TR 2000, 192 phase steps, 1 NEX
imaging time = 6.4 minutes
• At this rate, it would take 128 minutes to do
an average 20 slice exam.
• Because TR is typically much longer than
TE, we can acquire the data for the other
slices between the 90 degree RF pulses.
Image Acquisition Time

20. Multi-slice Imaging
echo

echo

echo

echo

slice 1
slice 2
slice 3
TR
TE

21. • The maximum number of slices that
can be obtained in a single acquisition
is calculated as follows:
Multi-slice Imaging
 
TR
TE
msec
msec + C
C msec
 
10 20

22. k-space Traversal
• The most important phase encoding
information is centered around the
middle of k-space.
• Typically, k-space is filled in an orderly
manner, beginning with the returned
echos obtained at the maximum negative
y gradient strength and continuing to the
maximum positive value.

23. • For images obtained with less than
256 views, the number of phase
encodings is evenly divided between
positive and negative values centered
around zero.
• Images reconstructed with less than
256 phase encodings have less detail in
the phase encoding direction.
k-space Traversal

24. kx
ky
256
2
5
6
256
1
2
8
256
1
2
8
decreased resolution

25. • Because k-space is symmetrical, one
half of the space can be determined
from knowledge of the other half.
• Imaging time can be reduced by a
factor of 2 by collecting either the
positive or the negative phase
encodings and filling the remainder of
k-space with the mirrored data.
Half Fourier Imaging

26. Half Fourier Imaging
kx
ky
256
2
5
6
kx
ky
256
1
2
8
full resolution

27. • This technique is sometimes referred
to as ‘half NEX’ imaging or ‘PCS’
(phase conjugate symmetry).
• Penalty: reduced signal decreases the
signal to noise ratio, typically by a
factor of 0.71.
Half Fourier Imaging

28. • The frequency half of k-space can also
be mirrored.
• This technique is called fractional
echo or ‘RCS’ (read conjugate
symmetry).
• Decreased read time enables more
slices per acquisition at the expense of
reduced signal.
Half Fourier Imaging

29. Half Fourier Imaging
kx
ky
256
2
5
6
256
kx
ky
1
2
8
normal phase symmetry
kx
ky
128
2
5
6
read symmetry

30. kx
ky
128
1
2
8 ?
128
kx
ky
2
5
6
128
kx
ky
1
9
2
128
kx
ky
1
2
8

31. 3D Acquisition
• 3D is an extension of the 2D technique.
advantages:
true contiguous slices
very thin slices (< 1 mm)
no partial volume effects
volume data acquisition
disadvantages:
gradient echo imaging only
(3D FSE now available)
motion sensitive

32. 3D Acquisition
• no slice select gradient
• entire volume of tissue is excited
• second phase encoding gradient
replaces the slice select gradient
• after the intial RF pulse (), both y
and z gradients are applied, followed
by application of the x gradient
during readout (echo)

33. • the z gradient is changed only after all
of the y gradient phase encodes have
generated an echo, then the z gradient
is stepped and the y gradient phase
encodes are repeated
3D Acquisition
   
TR number phase encodings number phase encodings NEX
msec    
1 2
60,000

34. 3D Imaging
RF
z gradient
echo

echo

echo

y gradient
x gradient
slice select
phase
readout

35. 3D Imaging
kx
ky
256
2
5
6



z step 1
z step 4
z step N
3D k-space