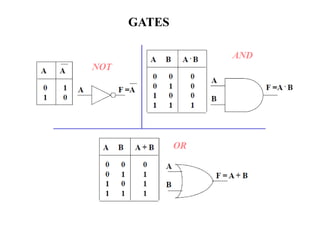
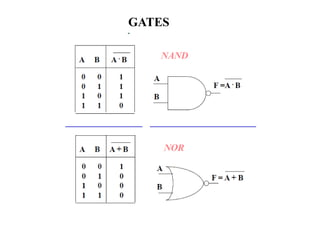
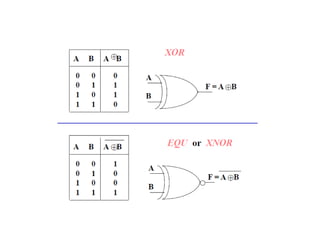
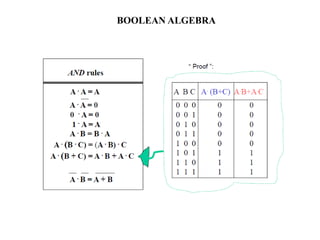
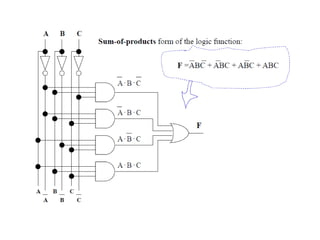
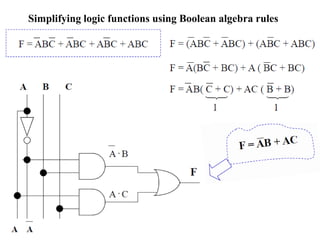
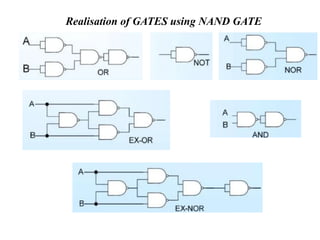
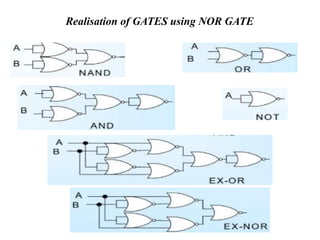
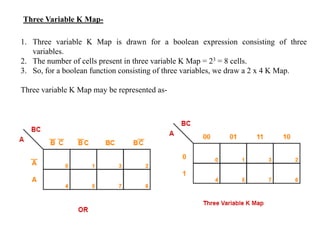
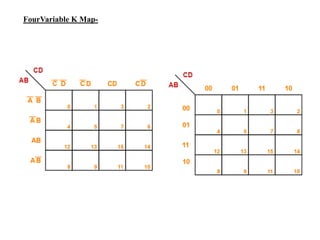
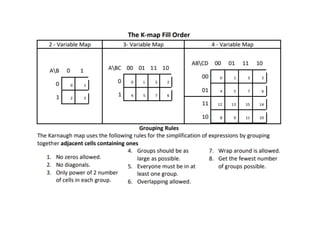
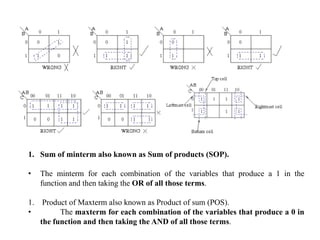
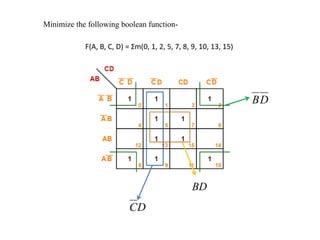
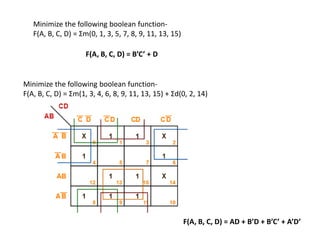
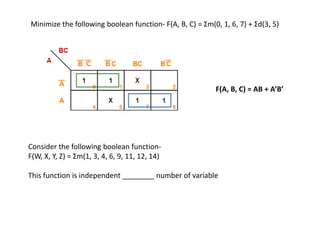
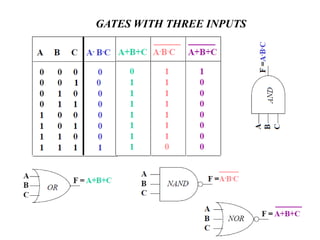
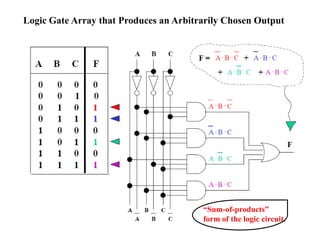
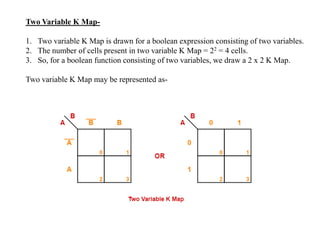
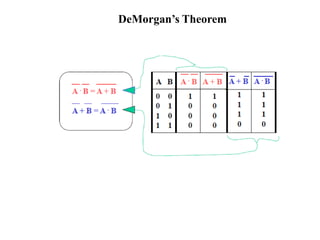
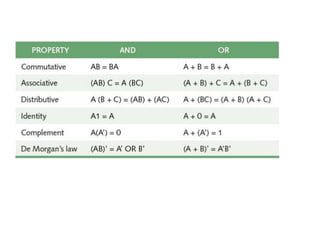
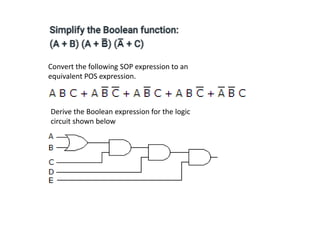
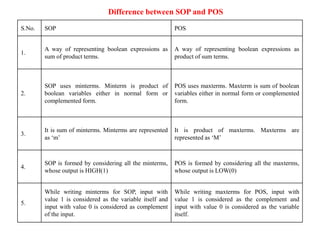
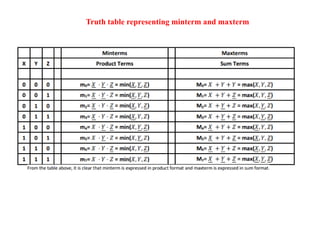
1. The document discusses digital logic circuits and their use of binary logic with 0 representing false and 1 representing true. 2. It explains that complex digital logic circuits like computers can be built using basic logic gates that perform operations like NOT, AND, OR, etc. 3. Boolean algebra is used as a formal tool to describe and design complex binary logic circuits using gates.

1. LOGIC OPERATIONS AND TRUTH TABLES
1. Digital logic circuits handle data encoded in binary form, i.e.
signals that have only two values, 0 and 1.
2. Binary logic dealing with “true” and “false” comes in handy to
describe the behaviour of these circuits: 0 is usually associated
with “false” and 1 with “true.”
3. Quite complex digital logic circuits (e.g. entire computers) can be
built using a few types of basic circuits called gates, each
performing a single elementary logic operation : NOT, AND, OR,
NAND, NOR, etc..
4. Boole‟s binary algebra is used as a formal / mathematical tool to
describe and design complex binary logic circuits

2. GATES

3. GATES

5. BOOLEAN ALGEBRA

8. BOOLEAN ALGEBRA

9. DeMorgan’s Theorem

11. GATES WITH THREE INPUTS

12. Logic Gate Array that Produces an Arbitrarily Chosen Output
“Sum-of-products”
form of the logic circuit.

14. Simplifying logic functions using Boolean algebra rules

15. Realisation of GATES using NAND GATE

16. Realisation of GATES using NOR GATE

17. Convert the following SOP expression to an
equivalent POS expression.
Derive the Boolean expression for the logic
circuit shown below

18. The minimized form of the logical expression

20. S.No. SOP POS
1.
A way of representing boolean expressions as
sum of product terms.
A way of representing boolean expressions as
product of sum terms.
2.
SOP uses minterms. Minterm is product of
boolean variables either in normal form or
complemented form.
POS uses maxterms. Maxterm is sum of boolean
variables either in normal form or complemented
form.
3.
It is sum of minterms. Minterms are represented
as „m‟
It is product of maxterms. Maxterms are
represented as „M‟
4.
SOP is formed by considering all the minterms,
whose output is HIGH(1)
POS is formed by considering all the maxterms,
whose output is LOW(0)
5.
While writing minterms for SOP, input with
value 1 is considered as the variable itself and
input with value 0 is considered as complement
of the input.
While writing maxterms for POS, input with
value 1 is considered as the complement and
input with value 0 is considered as the variable
itself.
Difference between SOP and POS

21. Truth table representing minterm and maxterm

22. Steps to solve expression using the K-map
1. Select K-map according to the number of variables.
2. Identify minterms or maxterms as given in the problem.
3. For SOP put 1‟s in blocks of K-map respective to the minterms (0‟s
elsewhere).
4. For POS put 0‟s in blocks of K-map respective to the maxterms(1‟s
elsewhere).
5. Make rectangular groups containing total terms in power of two like 2,4,8
..(except 1) and try to cover as many elements as you can in one group.
6. From the groups made in step 5 find the product terms and sum them up for
SOP form.
The Karnaugh Map also called as K Map is a graphical representation that
provides a systematic method for simplifying the boolean expressions.
Karnaugh Map-
• For a boolean expression consisting of n-variables, number of cells
required in K Map = 2n cells.

23. Two Variable K Map-
1. Two variable K Map is drawn for a boolean expression consisting of two variables.
2. The number of cells present in two variable K Map = 22 = 4 cells.
3. So, for a boolean function consisting of two variables, we draw a 2 x 2 K Map.
Two variable K Map may be represented as-

24. Three Variable K Map-
1. Three variable K Map is drawn for a boolean expression consisting of three
variables.
2. The number of cells present in three variable K Map = 23 = 8 cells.
3. So, for a boolean function consisting of three variables, we draw a 2 x 4 K Map.
Three variable K Map may be represented as-

25. FourVariable K Map-

27. Rule 1:
1. We can either group 0‟s with 0‟s or 1‟s with 1‟s but we can not group 0‟s and 1‟s
together.
2. X representing don‟t care can be grouped with 0‟s as well as 1‟s.
3. There is no need of separately grouping X’s i.e. they can be ignored if all 0’s and
1’s are already grouped.
Rule-02:
Groups may overlap each other.
Rule-03:
We can only create a group whose number of cells can be represented in the power of 2.
In other words, a group can only contain 2n i.e. 1, 2, 4, 8, 16 and so on number of cells.
Rule-04:
Groups can be only either horizontal or vertical.
We can not create groups of diagonal or any other shape.
Rule-05:
Each group should be as large as possible.
Opposite grouping and corner grouping are allowed.

28. 1. Sum of minterm also known as Sum of products (SOP).
• The minterm for each combination of the variables that produce a 1 in the
function and then taking the OR of all those terms.
1. Product of Maxterm also known as Product of sum (POS).
• The maxterm for each combination of the variables that produce a 0 in
the function and then taking the AND of all those terms.

29. Minimize the following boolean function-
F(A, B, C, D) = Σm(0, 1, 2, 5, 7, 8, 9, 10, 13, 15)
CD
BD
BD

30. Minimize the following boolean function-
F(A, B, C, D) = Σm(0, 1, 3, 5, 7, 8, 9, 11, 13, 15)
F(A, B, C, D) = B’C’ + D
Minimize the following boolean function-
F(A, B, C, D) = Σm(1, 3, 4, 6, 8, 9, 11, 13, 15) + Σd(0, 2, 14)
F(A, B, C, D) = AD + B’D + B’C’ + A’D’

31. Minimize the following boolean function- F(A, B, C) = Σm(0, 1, 6, 7) + Σd(3, 5)
F(A, B, C) = AB + A’B’
Consider the following boolean function-
F(W, X, Y, Z) = Σm(1, 3, 4, 6, 9, 11, 12, 14)
This function is independent ________ number of variable

32. Map the following SOP expression on a Karnaugh maP
Map the following standard POS expression on a Karnaugh map:

33. Find the minimum product of sums of the following expression
Y ABC ABC
 

34. Write minterm and maxterm Boolean functions expressed by f (A B C) = Π( 0, 3, 7)
Write a simplified maxterm Boolean expression for Π (0, 4, 5, 6, 7, 10, 14) using the
Karnaugh mapping method.