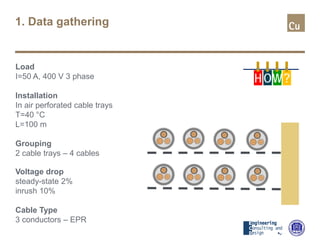
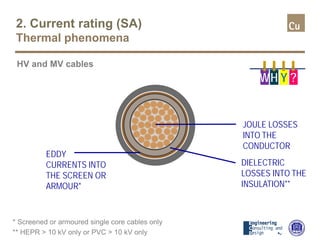
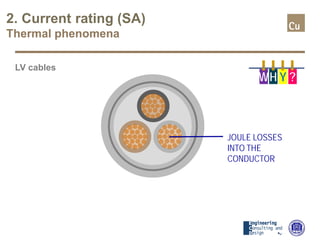
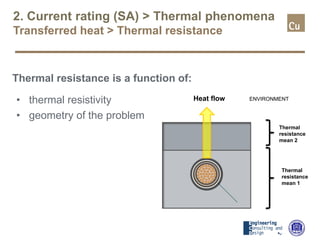
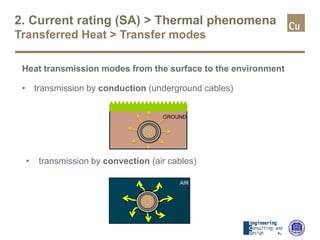
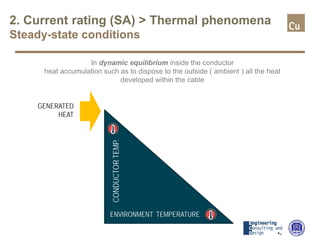
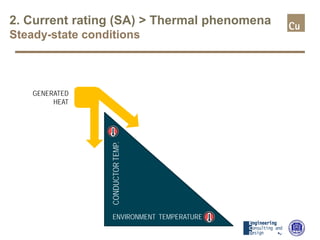
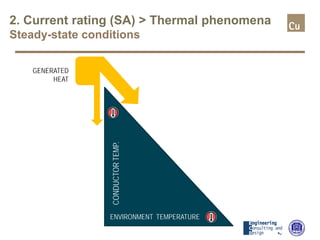
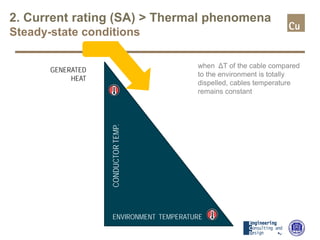
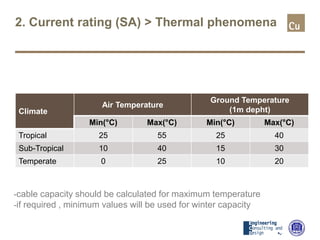
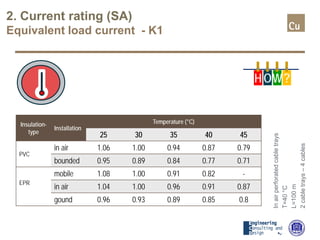
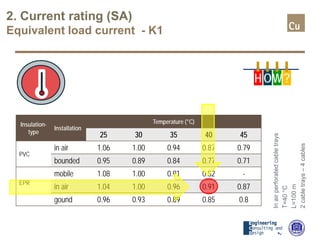
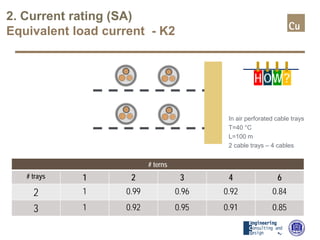
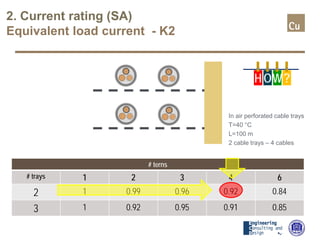
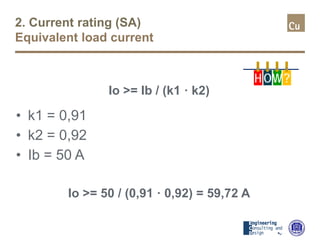
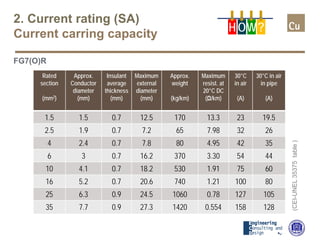
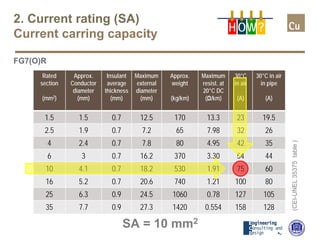
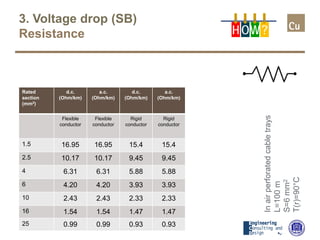
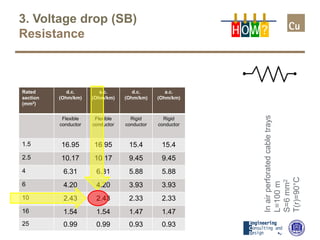
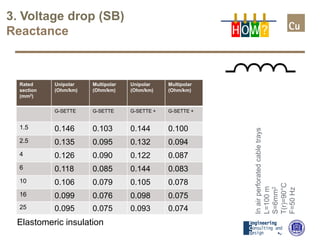
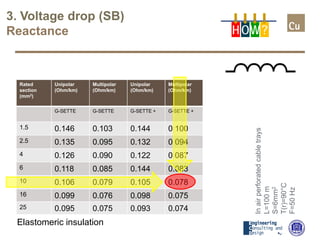
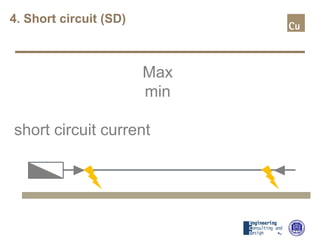
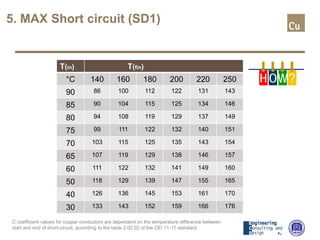
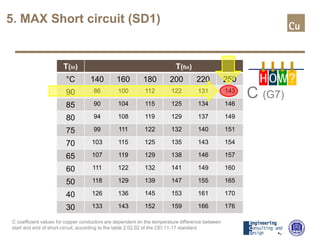
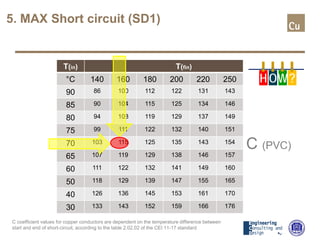
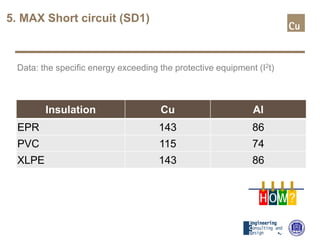
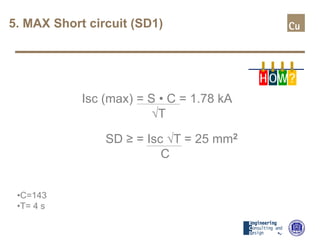
The document provides a comprehensive overview of cable sizing, detailing the process of selecting appropriate electrical cable sizes based on various parameters such as current rating, voltage drop, and installation conditions. It outlines the necessary data collection methods, including cable material, insulation type, installation method, and environmental factors. The document also elaborates on factors affecting current-carrying capacity and voltage drop, along with specific calculations and standards to guide the sizing process.

1. Angelo Baggini, angelo.baggini@unibg.it, Bergamo University - Engineering Department
Via Marconi 5, 24044 Dalmine (BG) – Italy
Principles of Cable Sizing

2. Introduction
Cable sizing vs Cable selection
Cable sizing is the
process of selecting
appropriate sizes for
electrical power cable
conductors.
the process of
selecting appropriate
sizes for electrical
power cable
conductors
Cable sizing is the
process of selecting
appropriate sizes for
electrical power cable
conductors.
the process of
selecting the
appropriate type of
cable

3. Process of cable sizing
1. Gather data about the cable, its installation conditions, the load that
it will carry
2. Determine the minimum cable size based on current rating
(continuous current carrying capacity) SA
3. Determine the minimum cable size based on voltage drop SB
4. Determine the minimum cable size based on inrush current SC
5. Determine the minimum cable size based on short circuit
temperature rise SD
6. Select the cable based on the largest of the sizes calculated in
the steps above S = MAX(SA, SB, SC, SD)

4. 1. Data gathering
Basic cable data
Load data
Cable installation

5. 1. Data gathering
LOAD DATA
Number of phases
three phase or single phase
Voltage
Rated voltage, allowed voltage drops
Full load current (A) or power (kW or kVA)
Full load power factor (pu)
Length of line
from source to load - this length should be as close as possible to the actual
route of the cable and include enough contingency for vertical drops / rises and
termination of the cable tails

6. 1. Data gathering
BASIC CABLE DATA
• Conductor material
Cu or Al
• Insulation or cable type
PVC, XLPE, EPR (IEC cables),
TW, THHW, XHH, etc. (NEC cables)
• Number of cores
1X, 2X, 3X … or 3G, 4G …

7. 1. Data gathering
CABLE INSTALLATION
Installation method
cable tray / ladder, in conduit / raceways, on a wall, in air, directly
buried, etc
Ambient or soil temperature at the installation site
Cable grouping
number of other cables bunched together or installed in the same area
Cable spacing
whether cables are installed touching or spaced
Soil thermal resistivity
(for underground cables)
Trefoil or laid flat
(for single core three-phase cables)

8. Load
I=50 A, 400 V 3 phase
Installation
In air perforated cable trays
T=40 °C
L=100 m
Grouping
2 cable trays – 4 cables
Voltage drop
steady-state 2%
inrush 10%
Cable Type
3 conductors – EPR
H OW?
1. Data gathering

9. 2. Current rating (SA)
DATA:
• installation method
• cable type
• load sustained current (Ib)
Selection from the Standards of the:
• base current rating (Io)
• correction factors:
• k1 for variation in ambient temperature
• k2 for adjacent circuits
• k3 for variation in burial depth
• k4 for ground thermal resistance
The maximum sustained current rating (Iz):
Iz (S) >= Io · k1 · k2 · k3 · k4 >= Ib

10. 2. Current rating (SA)
Thermal phenomena
HV and MV cables
WH Y ?
JOULE LOSSES
INTO THE
CONDUCTOR
DIELECTRIC
LOSSES INTO THE
INSULATION**
EDDY
CURRENTS INTO
THE SCREEN OR
ARMOUR*
* Screened or armoured single core cables only
** HEPR > 10 kV only or PVC > 10 kV only

11. 2. Current rating (SA)
Thermal phenomena
LV cables
WH Y ?
JOULE LOSSES
INTO THE
CONDUCTOR

12. 2. Current rating (SA)
Thermal phoenomena
WH Y ?
Gathered into the
conductor increasing
temperature
Tramsmitted to the
environment by
conduction and
convention
Heat is

13. 2. Current rating (SA)
Thermal phoenomena
WH Y ?
Gathered into the
conductor increasing
temperature
Tramsmitted to the
environment by
conduction and
convention
Heat is

14. 2. Current rating (SA)
Thermal phoenomena
WH Y ?
Gathered into the
conductor increasing
temperature
Tramsmitted to the
environment by
conduction and
convention
Heat is

15. 2. Current rating (SA) > Thermal phenomena
Accumulated heat
The amount of heat accumulated in the conductor depends on
the thermal capacity
Thermal capacity is function of:
• Specific heat capacity of the material ( c )
• cCu = 3,45 x 106 J/K m3
• cAl = 2,50 x 106 J/K m3
• Volume (conductor section)

16. 2. Current rating (SA) > Thermal phenomena
Transferred heat
The quantity of transferred heat depends on:
• heat transfer modes (convection, conduction)
• thermal resistance of the "circuit"

17. 2. Current rating (SA) > Thermal phenomena
Transferred heat > Thermal resistance
Thermal resistance is a function of:
• thermal resistivity
• geometry of the problem
Heat flow ENVIRONMENT
Thermal
resistance
mean 2
Thermal
resistance
mean 1

18. 2. Current rating (SA) > Thermal phenomena
Transferred heat > Thermal resistance
Thermal insulating effect of electrical insulation and cable sheaths shall
be calculated by using construction data and thermal resistivities.
For single-core cables with a metal sheath for example:
Tk=T1+T2= (Q1/2π) ln(d1/dL)+ (Q3/2π) ln(d3/dM)
dM d1 dL d3

19. 2. Current rating (SA) > Thermal phenomena
Transferred Heat > Transfer modes
Heat transmission modes from the surface to the environment
• transmission by conduction (underground cables)
• transmission by convection (air cables)
GROUND
AIR

20. 2. Current rating (SA) > Thermal phenomena
Steady-state conditions
CONDUCTORTEMP.
ENVIRONMENT TEMPERATURE
GENERATED
HEAT
In dynamic equilibrium inside the conductor
heat accumulation such as to dispose to the outside ( ambient ) all the heat
developed within the cable

21. 2. Current rating (SA) > Thermal phenomena
Steady-state conditions
CONDUCTORTEMP.
ENVIRONMENT TEMPERATURE
GENERATED
HEAT

22. 2. Current rating (SA) > Thermal phenomena
Steady-state conditions
CONDUCTORTEMP.
ENVIRONMENT TEMPERATURE
GENERATED
HEAT

23. 2. Current rating (SA) > Thermal phenomena
Steady-state conditions
CONDUCTORTEMP.
ENVIRONMENT TEMPERATURE
GENERATED
HEAT
when ΔT of the cable compared
to the environment is totally
dispelled, cables temperature
remains constant

24. 2. Current rating (SA) > Thermal phenomena
• Rating calculation therefore involves the solution of a heat
problem
• current-carrying capacity is a characteristic of a cable :
• of a certain type
• of a certain section
• in a certain installation
( )
I
nR R R R
z
a
c a x
=
−
+ +
θ θ
ϑ ϑ ϑ
lim

25. 2. Current rating (SA) > Thermal phenomena
Climate
Air Temperature
Ground Temperature
(1m depht)
Min(°C) Max(°C) Min(°C) Max(°C)
Tropical 25 55 25 40
Sub-Tropical 10 40 15 30
Temperate 0 25 10 20
-cable capacity should be calculated for maximum temperature
-if required , minimum values ​​will be used for winter capacity

26. Load
I=50 A, 400 V 3 phase
Installation
In air perforated cable trays
T=40 °C
L=100 m
Grouping
2 cable trays – 4 cables
Voltage drop
steady-state 2%
inrush 10%
Cable Type
3 conductors – EPR
H OW?
2. Current rating (SA)

27. 2. Current rating (SA)
Equivalent load current
• k1 for variation in ambient temperature
• k2 for adjacent circuits
• k3 for variation in burial depth
• K4 for ground thermal resistance
𝐼𝐼𝐼𝐼 ≥
𝐼𝐼𝑏𝑏
(k1 · k2 · k3 · k4 )
H OW?

28. Inairperforatedcabletrays
T=40°C
L=100m
2cabletrays–4cables
2. Current rating (SA)
Equivalent load current - K1
Insulation-
type
Installation
Temperature (°C)
25 30 35 40 45
PVC
in air 1.06 1.00 0.94 0.87 0.79
bounded 0.95 0.89 0.84 0.77 0.71
EPR
mobile 1.08 1.00 0.91 0.82 -
in air 1.04 1.00 0.96 0.91 0.87
gound 0.96 0.93 0.89 0.85 0.8
H OW?

29. Inairperforatedcabletrays
T=40°C
L=100m
2cabletrays–4cables
2. Current rating (SA)
Equivalent load current - K1
Insulation-
type
Installation
Temperature (°C)
25 30 35 40 45
PVC
in air 1.06 1.00 0.94 0.87 0.79
bounded 0.95 0.89 0.84 0.77 0.71
EPR
mobile 1.08 1.00 0.91 0.82 -
in air 1.04 1.00 0.96 0.91 0.87
gound 0.96 0.93 0.89 0.85 0.8
H OW?

30. # terns
# trays 1 2 3 4 6
2 1 0.99 0.96 0.92 0.84
3 1 0.92 0.95 0.91 0.85
2. Current rating (SA)
Equivalent load current - K2
In air perforated cable trays
T=40 °C
L=100 m
2 cable trays – 4 cables
H OW?

31. # terns
# trays 1 2 3 4 6
2 1 0.99 0.96 0.92 0.84
3 1 0.92 0.95 0.91 0.85
2. Current rating (SA)
Equivalent load current - K2
In air perforated cable trays
T=40 °C
L=100 m
2 cable trays – 4 cables
H OW?

32. 2. Current rating (SA)
Equivalent load current
Io >= Ib / (k1 · k2)
• k1 = 0,91
• k2 = 0,92
• Ib = 50 A
Io >= 50 / (0,91 · 0,92) = 59,72 A
H OW?

33. Rated
section
(mm2)
Approx.
Conductor
diameter
(mm)
Insulant
average
thickness
(mm)
Maximum
external
diameter
(mm)
Approx.
weight
(kg/km)
Maximum
resist. at
20°C DC
(Ω/km)
30°C
in air
(A)
30°C in air
in pipe
(A)
1.5 1.5 0.7 12.5 170 13.3 23 19.5
2.5 1.9 0.7 7.2 65 7.98 32 26
4 2.4 0.7 7.8 80 4.95 42 35
6 3 0.7 16.2 370 3.30 54 44
10 4.1 0.7 18.2 530 1.91 75 60
16 5.2 0.7 20.6 740 1.21 100 80
25 6.3 0.9 24.5 1060 0.78 127 105
35 7.7 0.9 27.3 1420 0.554 158 128
(CEI-UNEL35375table)
2. Current rating (SA)
Current carring capacity
FG7(O)R
H OW?

34. Rated
section
(mm2)
Approx.
Conductor
diameter
(mm)
Insulant
average
thickness
(mm)
Maximum
external
diameter
(mm)
Approx.
weight
(kg/km)
Maximum
resist. at
20°C DC
(Ω/km)
30°C
in air
(A)
30°C in air
in pipe
(A)
1.5 1.5 0.7 12.5 170 13.3 23 19.5
2.5 1.9 0.7 7.2 65 7.98 32 26
4 2.4 0.7 7.8 80 4.95 42 35
6 3 0.7 16.2 370 3.30 54 44
10 4.1 0.7 18.2 530 1.91 75 60
16 5.2 0.7 20.6 740 1.21 100 80
25 6.3 0.9 24.5 1060 0.78 127 105
35 7.7 0.9 27.3 1420 0.554 158 128
(CEI-UNEL35375table)
2. Current rating (SA)
Current carring capacity
FG7(O)R
H OW?
SA = 10 mm2

35. 3. Voltage drop (SB)
DATA:
• Maximum voltage drop (standard)
• Cable R and X
• Line length (L)
• Load Current I (standard)
• Phase displacement (ϕ) (standard)
∆V(S) = K L I (R cosϕ + X sinϕ) < ∆VM
K = 2 for single-phase lines
K = √(3) for tree-phase lines

36. Load
I=50 A, 400 V 3 phase
Installation
In air perforated cable trays
T=40 °C
L=100 m
Grouping
2 cable trays – 4 cables
Voltage drop
steady-state 2%
inrush 10%
Cable Type
3 conductors – EPR
H OW?
3. Voltage drop (SB)

37. Inairperforatedcabletrays
L=100m
S=6mm2
T(r)=90°C
3. Voltage drop (SB)
Resistance
Rated
section
(mm2)
d.c.
(Ohm/km)
a.c.
(Ohm/km)
d.c.
(Ohm/km)
a.c.
(Ohm/km)
Flexible
conductor
Flexible
conductor
Rigid
conductor
Rigid
conductor
1.5 16.95 16.95 15.4 15.4
2.5 10.17 10.17 9.45 9.45
4 6.31 6.31 5.88 5.88
6 4.20 4.20 3.93 3.93
10 2.43 2.43 2.33 2.33
16 1.54 1.54 1.47 1.47
25 0.99 0.99 0.93 0.93
H OW?

38. Inairperforatedcabletrays
L=100m
S=6mm2
T(r)=90°C
3. Voltage drop (SB)
Resistance
Rated
section
(mm2)
d.c.
(Ohm/km)
a.c.
(Ohm/km)
d.c.
(Ohm/km)
a.c.
(Ohm/km)
Flexible
conductor
Flexible
conductor
Rigid
conductor
Rigid
conductor
1.5 16.95 16.95 15.4 15.4
2.5 10.17 10.17 9.45 9.45
4 6.31 6.31 5.88 5.88
6 4.20 4.20 3.93 3.93
10 2.43 2.43 2.33 2.33
16 1.54 1.54 1.47 1.47
25 0.99 0.99 0.93 0.93
H OW?

39. Inairperforatedcabletrays
L=100m
S=6mm2
T(r)=90°C
F=50Hz
3. Voltage drop (SB)
Reactance
Rated
section
(mm2)
Unipolar
(Ohm/km)
Multipolar
(Ohm/km)
Unipolar
(Ohm/km)
Multipolar
(Ohm/km)
G-SETTE G-SETTE G-SETTE + G-SETTE +
1.5 0.146 0.103 0.144 0.100
2.5 0.135 0.095 0.132 0.094
4 0.126 0.090 0.122 0.087
6 0.118 0.085 0.144 0.083
10 0.106 0.079 0.105 0.078
16 0.099 0.076 0.098 0.075
25 0.095 0.075 0.093 0.074
Elastomeric insulation
H OW?

40. Inairperforatedcabletrays
L=100m
S=6mm2
T(r)=90°C
F=50Hz
3. Voltage drop (SB)
Reactance
Rated
section
(mm2)
Unipolar
(Ohm/km)
Multipolar
(Ohm/km)
Unipolar
(Ohm/km)
Multipolar
(Ohm/km)
G-SETTE G-SETTE G-SETTE + G-SETTE +
1.5 0.146 0.103 0.144 0.100
2.5 0.135 0.095 0.132 0.094
4 0.126 0.090 0.122 0.087
6 0.118 0.085 0.144 0.083
10 0.106 0.079 0.105 0.078
16 0.099 0.076 0.098 0.075
25 0.095 0.075 0.093 0.074
Elastomeric insulation
H OW?

41. 3. Voltage drop (SB)
Size selection
∆V(S) = K L I (R cosϕ + X sinϕ) < ∆VM
K = √(3)
R(6)= 2.430 (ohm/km)
X(6)=0.078 (ohm/km)
L=100 m
cosϕ =0.8
S= 6 mm2 - ∆V(6) =17.24 V ∆V% = ∆V/V = 4 .31% > 2%
S=10 mm2  ∆V% = 4.3 % >2%
S=16 mm2  ∆V% = 2.7% > 2%
S=25 mm2  ∆V% = 1.8%< 2% ∆V(25)= 7.25 V
H OW?

42. 3. Voltage drop (SB)
Inrush Current
∆V(r) = K L I (R cosϕ + X sinϕ)
∆V<= ∆V(max on start up)
DATA
•I = start-up current
•cosϕ=0.2 for motors / cosϕ=0 for capacitors
•K = √(3) for tree-phase / K = 2 for single-phase
•R= resistance in the service temperature
•X= reactance in service of the cable (AC lines only)
•L= lenght

43. Load
I=50 A, 400 V 3 phase
Installation
In air perforated cable trays
T=40 °C
L=100 m
Grouping
2 cable trays – 4 cables
Voltage drop
steady-state 2%
inrush 10%
Cable Type
3 conductors – EPR
H OW?
3. Voltage drop inrush current (SC)

44. 3. Voltage drop inrush current (SC)
∆V(r%)= (14.05*100) = 3.5% < 10%
400
•I(r) = 6*I = 300 A
•cosϕ=0.2
•K = √(3)
•R= 0.99 Ohm/km
∆V(r) = √(3)*0.1*300* (0.99*0.2 + 0.074*0.98)= 14.05 V
•X=0.074 Ohm/km
•L=100 m
•S=25 mm 2
•INRUSH <=10% V
minimum section
SC=25mm 2

45. 4. Short circuit (SD)
Max
min
short circuit current

46. 4. MAX Short circuit (SD)
S ≥ = Isc √T
C
• T = short circuit duration (s)
• S = cross-section of copper conductor (mm2)
• Icc = short circuit current (A)
• C is a coefficient depending on initial and final temperature
The max short circuit current accepted by a conductor with section S
is calulated with the following formula
Isc (max) = S • C
√T

47. Load
I=50 A, 400 V 3 phase
Installation
In air perforated cable trays
T=40 °C
L=100 m
Grouping
2 cable trays – 4 cables
Voltage drop
steady-state 2%
inrush 10%
Cable Type
3 conductors – EPR
H OW?
4. MAX Short circuit (SD)

48. 5. MAX Short circuit (SD1)
C coefficient values for copper conductors are dependent on the temperature difference between
start and end of short-circuit, according to the table 2.02.02 of the CEI 11-17 standard
T(in) T(fin)
°C 140 160 180 200 220 250
90 86 100 112 122 131 143
85 90 104 115 125 134 146
80 94 108 119 129 137 149
75 99 111 122 132 140 151
70 103 115 125 135 143 154
65 107 119 129 138 146 157
60 111 122 132 141 149 160
50 118 129 139 147 155 165
40 126 136 145 153 161 170
30 133 143 152 159 166 176
H OW?

49. 5. MAX Short circuit (SD1)
C coefficient values for copper conductors are dependent on the temperature difference between
start and end of short-circuit, according to the table 2.02.02 of the CEI 11-17 standard
T(in) T(fin)
°C 140 160 180 200 220 250
90 86 100 112 122 131 143
85 90 104 115 125 134 146
80 94 108 119 129 137 149
75 99 111 122 132 140 151
70 103 115 125 135 143 154
65 107 119 129 138 146 157
60 111 122 132 141 149 160
50 118 129 139 147 155 165
40 126 136 145 153 161 170
30 133 143 152 159 166 176
C (G7)
H OW?

50. 5. MAX Short circuit (SD1)
C coefficient values for copper conductors are dependent on the temperature difference between
start and end of short-circuit, according to the table 2.02.02 of the CEI 11-17 standard
T(in) T(fin)
°C 140 160 180 200 220 250
90 86 100 112 122 131 143
85 90 104 115 125 134 146
80 94 108 119 129 137 149
75 99 111 122 132 140 151
70 103 115 125 135 143 154
65 107 119 129 138 146 157
60 111 122 132 141 149 160
50 118 129 139 147 155 165
40 126 136 145 153 161 170
30 133 143 152 159 166 176
C (PVC)
H OW?

51. 5. MAX Short circuit (SD1)
Data: the specific energy exceeding the protective equipment (I2t)
Insulation Cu Al
EPR 143 86
PVC 115 74
XLPE 143 86
H OW?

52. 5. MAX Short circuit (SD1)
Isc (max) = S • C = 1.78 kA
√T
SD ≥ = Isc √T = 25 mm2
C
•C=143
•T= 4 s
H OW?

53. 5. Min short circuit current
neutral NOT distributed conductor
𝑰𝑰𝑰𝑰𝑰𝑰 =
𝟎𝟎, 𝟓𝟓 𝑼𝑼
𝟏𝟏, 𝟓𝟓 �
𝟐𝟐𝟐𝟐
𝑺𝑺
• U = line voltage supplied
• ρ = resistivity of the conductor
compounds at 20 °C, ohm • mm2
(0,018 for Cu - 0,027 for Al)
• L = length of protected conductor
• S = conductor cross-section
• Icc = short-circuit current
neutral distributed conductor
𝑰𝑰𝑰𝑰𝑰𝑰 =
𝟎𝟎, 𝟖𝟖 𝑼𝑼𝑼𝑼
𝟏𝟏, 𝟓𝟓 �(𝟏𝟏 + 𝒎𝒎)
𝑳𝑳
𝑺𝑺
• Uo = phase rating voltage
• m= ratio of the neutral
conductor resistance and the
phase conductor resistance

54. 6. Min Short circuit (SD2)
minimum short-circuit current
0,8 U 0.8 (400)
Icc(min) = = = 1.48 kA
1,5 ρ 2 L 1.5( 0.018) (8)
S
SD4= 25 mm2
Icc(min) 1,5 ρ 2 L
S= = 24.97 mm2  25 mm2
0.8 U
H OW?

55. 6. Min Short circuit (SD2)
neutral NOT distributed conductor
𝑰𝑰𝑰𝑰𝑰𝑰 =
𝟎𝟎,𝟓𝟓 𝑼𝑼
𝟏𝟏,𝟓𝟓 �𝟐𝟐𝟐𝟐
𝑺𝑺
=
𝟎𝟎,𝟓𝟓 𝟒𝟒𝟒𝟒𝟒𝟒
𝟏𝟏,𝟓𝟓 𝟎𝟎,𝟎𝟎𝟎𝟎𝟎𝟎
𝟐𝟐 𝟏𝟏𝟏𝟏𝟏𝟏
𝟐𝟐𝟐𝟐 𝟏𝟏𝟏𝟏^−𝟑𝟑
= 1,48 kA
H OW?

56. 6. Size selection
S = MAX(SA, SB, SC, SD)
S = MAX(10, 25, 25, 25)= 25 mm2
• Current rating (SA)
• Voltage drop (SB)
• Inrush current (SC)
• Short circuit (SD)
H OW?

57. Thank you
| Presentation title and date
For more information please contact
Angelo Baggini
Università di Bergamo
Dipartimento di Ingegneria
Viale Marconi 5,
24044 Dalmine (BG) Italy
email: angelo.baggini@unibg.it
ECD Engineering Consulting and Design
Via Maffi 21 27100 PAVIA Italy