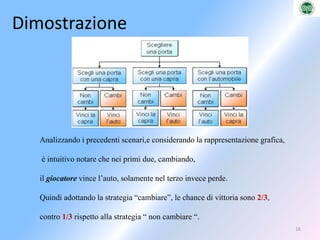
Il documento tratta dei modelli per la descrizione di processi probabilistici, presentando un approccio composizionale ai sistemi complessi attraverso automi a stati finiti e automi probabilistici. Si discute la necessità di una comunicazione tra componenti di sistemi distribuiti per superare le criticità dei modelli esistenti e per calcolare le probabilità di raggiungere stati critici. Viene infine illustrato il problema di Monty Hall, evidenziando come cambiare scelta possa aumentare le probabilità di vincita.

1. UNIVERSITA’ DEGLI STUDI DELL’INSUBRIAFACOLTA’DI SCIENZE MM.FF.NN.SCIENZE E TECNOLOGIE DELL’INFORMAZIONE MODELLI PER LA DESCRIZIONE DI PROCESSI PROBABILISTICIA cura di: Polidoro Alessio1

2. Obiettivo tesi: Entità autonome/agenti/moduli

3. Distribuiti

4. Comunicazioni di tipo sincrono/asincrono/broadcasting

5. Gerarchici

6. Probabilistici2Descrizione composizionale di sistemi “ complessi “ :

7. Automi a stati finitiFSA ≡ Controllo di un sistema dinamico sequenziale discreto. Rabin, Scott 1954 Mc Culloch, Pitts 1943Sistema dinamico discreto: S ≡ Q : insiemi degli stati q0 : stato iniziale Σ : alfabeto delle azioni δ : Σ x Q -> Q funzione di transizione F : insieme degli stati finaliNOTA: FSA + DATI ≡ Macchina di Turing3

8. 4Problema: Estendere la “classica” teoria degli Automi per modellare/verificare sistemi:Distribuiti

9. Temporizzati

10. Gerarchici

11. ProbabilisticiModelli probabilisticiAutoma probabilistico di Rabin Nel 1963, Michael O. Rabin introduce gli Automi Probabilistici, come generalizzazione di automi non deterministici. Un automa viene descritto attraverso Caratterizzato attraverso una matrice stocastica, definendo per ogni transizione esistente una probabilità, la quale quantifica la possibilità del suo verificarsi. La somma delle probabilità delle transizioni etichettate da un determinato simbolo dell’alfabeto uscenti da un determinato stato deve essere necessariamente uguale ad 1: Lo stato iniziale dell’automa probabilistico è dato tramite un vettore coordinata v , le cui componenti rappresentano le probabilità che il sistema si trovi in un determinato stato iniziale, avente valori zero per tutte le componenti tranne una.5

12. Modelli per sistemi distribuitiIdea: Un Sistema viene visto come una n-upla di sottosistemi S1, S2 , … , Sn interagenti tra loro.

13. Ogni componente locale è descritta da un automa a stati finiti.

14. L’automa globale, che descrive l’intero sistema, è ottenuto attraverso il prodotto delle componenti locali: gli stati globali raggiungibili sono il prodotto cartesiano degli insiemi degli stati locali ( problema dell’esplosione combinatoria degli stati). Le componenti locali, interagendo tra di loro, creano situazioni complesse.6

15. Modelli per sistemi distribuitiCriticità: L’approccio descritto non è composizionale, cioè ogni componente di base viene vista come un sistema chiuso, non predisposto alla comunicazione.7

16. Modelli per sistemi distribuitiIdea: Necessario adottare un approccio differente , simile a quello per circuiti, consistente nel considerare ogni singola componente come un sistema aperto, in grado di comunicare con altri ai quali è collegato. Un automa verrà quindi arricchito da esplicite interfacce di comunicazione . Le componenti di base, aperte alla comunicazione, verranno composte con opportune operazioni (serie, parallelo con e senza comunicazione, feedback), realizzando reti di automi complesse, in modo composizionale. 8