Download to read offline
Uploaded byimartini
Presentazione
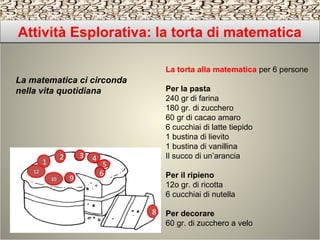
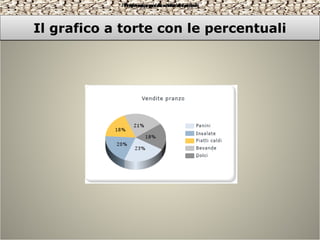
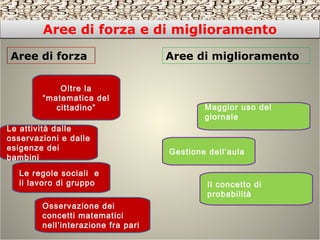
Il documento esplora l'importanza dell'insegnamento della matematica attraverso approcci pratici e quotidiani, come l'uso di giornali e attività legate alla vita reale, per aumentare motivazione e comprensione degli studenti. Viene evidenziato come la matematica sia fondamentale per affrontare le sfide moderne e garantire pari opportunità, nonché per lo sviluppo di abilità critiche nella risoluzione di problemi. Infine, vengono presentate unità didattiche strutturate per insegnare concetti matematici attraverso esperienze pratiche e stimolanti.
![Guida 1a [2012 2013]](https://cdn.slidesharecdn.com/ss_thumbnails/guida1a2012-2013-121015063728-phpapp02-thumbnail.jpg?width=640&height=640&fit=bounds)
![Guida 1A-3 [2009 - 2010]](https://cdn.slidesharecdn.com/ss_thumbnails/guida1a-32009-2010-100714234959-phpapp01-thumbnail.jpg?width=640&height=640&fit=bounds)
Presentazione
- 1. I NUMERI NELNOSTRO MONDO FARE MATEMATICA LEGGENDO I GIORNALI Maria Teresa Marrano Relatore: prof.ssa Supervisore: dott.ssa Ana Millán Gasca Loredana La Civita Scuola C.D. Via delle Quinqueremi (Roma - Lido di Ostia) Classe: IV
- 2. Uno sguardo allastoria Riflettere a scuola sulla matematica nel nostro mondo oltre la matematica del cittadino • I problemi • Elementi di statistica descrittiva • La matematica con i giornali La matematica nel lavoro e nell’organizzazioneLa matematica nel lavoro e nell’organizzazione • Il calcolo utile nell’evoluzione storica della matematica • La matematica pratica nella tradizione didattica europea • La matematica sociale e il problema della matematizzazione delle scienze non fisiche
- 3. Se si utilizzanoin classe giornali, cartine, orari dei treni ed altri elementi della quotidianità si potrà proporre agli alunni un approccio alternativo rispetto all’insegnamento tradizionale in modo da … • Avere maggiore consapevolezza • Aumentare la motivazione e l’interesse verso la disciplina • Diminuire le difficoltà di apprendimento … e divertirsi !!! I motivi del progettoI motivi del progetto Nel nostro mondo è imprescindibile saper ragionare per quantità, la matematica è nel cuore del trattamento dell’informazione quantitativa nella scienza, nella tecnologia, nell’economia. La competenza matematica risulta fondamentale nella consapevolezza del futuro cittadino, del consumatore e nella vita professionale … … ma la matematica ha anche un valore formativo per garantire a tutti pari opportunità
- 4. Attività Esplorativa: latorta di matematicaAttività Esplorativa: la torta di matematica 1 2 6 5 43 12 10 8 9 La torta alla matematica per 6 persone Per la pasta 240 gr di farina 180 gr. di zucchero 60 gr di cacao amaro 6 cucchiai di latte tiepido 1 bustina di lievito 1 bustina di vanillina Il succo di un’arancia Per il ripieno 12o gr. di ricotta 6 cucchiai di nutella Per decorare 60 gr. di zucchero a velo La matematica ci circonda nella vita quotidiana
- 5. Le Unità DidatticheLeUnità Didattiche 1. I numeri nel nostro mondo e nella storia Ordinare i numeri per misurare Il ruolo della matematica nel lavoro e nelle attività Le parole tabù I numeri della classe 2. Mettere ordine nei numeri I giornali e i numeri nel nostro mondo Le società nell’antichità: i censimenti I valori dei numeri e i tipi di numero I giornali e la gara 3. Organizzarsi con i numeri I grafici e le tabelle Organizzare i dati Il punteggio con le macchinine Organizzare il menù con i grafici 4. Le informazioni meteorologiche La tabella meteorologica sul giornale Organizzare un viaggio usando il giornale La temperatura dell’intera settimana Previsioni del tempo e la valigia La preparazione della merenda con il giornale La merenda salta dallo zaino 5. La gita al museo La scelta della località dal giornale Il calcolo del percorso
- 6. La prima unitàdidattica I numeri nel nostro mondo e nella storia La prima unità didattica I numeri nel nostro mondo e nella storia Ordinare i numeri per misurare Il ruolo della matematica nel lavoro e nelle attività …… I, II, III…X 1,2,3
- 7. Il paese deinon so … Un mondo senza matematica Il “paese dei non so” e le parole TabùIl “paese dei non so” e le parole Tabù Il paese dei non so …. In un tempo che … non so e in un posto che si trovava lontano ma non so quanto, vivono delle persone, quante … non so, che non conoscono e non hanno mai utilizzato la matematica, eppure si svegliano ogni mattina molto presto ma l’orario … non so, svolgono le loro attività, insomma vivono senza matematica. Prova a scrivere come immagini questo mondo
- 8. Le parole Tabù:i controlloriLe parole Tabù: i controllori
- 9. La costituzione deigruppiLa costituzione dei gruppi In classe ci sono 22 bambini e bisogna formare dei gruppi che abbiano minimo 4 bambini e massimo 5. Quanti gruppi si possono formare? “maestra, io faccio 22:4=5 con 2 che restano fuori e che poi li dividiamo tra i 4 gruppi” “maestra, ma perché non facciamo 3x4=12 e formiamo 3 gruppi da 4 e poi ci rimangono 10 bambini e formiamo altri 2 gruppi” 3 gruppi di 4 e 2 gruppi di 5 bambini
- 10. I numeri neigiornali La seconda Unità Didattica Mettere ordine nei numeri La seconda Unità Didattica Mettere ordine nei numeri Ma quanti numeri ci sono in un giornale Numeri per contare Numeri per ordinare Numeri per identificare
- 11. La terza UnitàDidattica Organizzarsi con i numeri La terza Unità Didattica Organizzarsi con i numeri Organizzare i dati Gruppo 1 Un gelataio vuole vendere in una classe con 22 bambini dei gelati, ma può portare un solo gusto tra crema, cioccolato e frutta, come farà a scegliere il gusto preferito dai bambini e cercare così di guadagnare di più Dal quesito all’indagine
- 12. LA MATEMATICA, LAGARA E LE REGOLELA MATEMATICA, LA GARA E LE REGOLE Il punteggio della gara e la sua rappresentazione con l’istogramma
- 13. Organizzare il menùcon i grafici a tortaOrganizzare il menù con i grafici a torta Preferenza per la scelta dei primi Pastaal sugo Pastacon verdure Pastacon carne Preferenza per la scelta dei secondi Carne Fromaggi Verdure Preferenza per i primi Preferenza per i secondi Preferenza per la scelta dei dolci Torta Gelato Creme Preferenza per i dolci
- 14. Il grafico atorte con le percentualiIl grafico a torte con le percentuali Preferenza per la scelta dei primiPreferenza per la scelta dei secondiPreferenza per la scelta dei dolci
- 15. Organizzare un viaggio guardandoil giornale e … La temperatura e il concetto della media La preparazione della valigia La quarta unità didattica: le informazioni meteorologicheLa quarta unità didattica: le informazioni meteorologiche
- 16. Organizzare un viaggio guardandoil giornale e … La temperatura e il concetto della media La preparazione della valigia La quarta unità didattica: le informazioni meteorologicheLa quarta unità didattica: le informazioni meteorologiche
- 17. La quarta unitàdidatticaLa quarta unità didattica Che dolce ci piace portare in viaggio? … al grafico dalla tabella …
- 18. L’età mediaL’età media Calcolodell'età media di fratelli e sorelle di un bambino … e poi della classe
- 19. La quarta UnitàDidatticaLa quarta Unità Didattica I dolci alla matematica
- 20. La quinta unitàdidattica La gita al museo La quinta unità didattica La gita al museo Partendo dai giornali e depliant … … Si va al museo e si calcola il percorso La durata del viaggio a velocità costante in funzione dello spazio da percorrere Il treno della linea rossa impiega 5 minuti per raggiungere ogni fermata; la metro della linea viola ne impiega 4 e quella della linea gialla 2. Indicare il tempo che si impiega per arrivare ai Musei
- 21. Aree di forzae di miglioramentoAree di forza e di miglioramento Oltre la “matematica del cittadino” Le attività dalle osservazioni e dalle esigenze dei bambini Aree di forza Osservazione dei concetti matematici nell’interazione fra pari Le regole sociali e il lavoro di gruppo Aree di miglioramento Il concetto di probabilità Maggior uso del giornale Gestione dell’aula
- 22. Osservazione iniziale • Notevoleutilizzo dei concetti matematici Osservazione finale • Notevole utilizzo dei concetti matematici • Arricchimento nella tipologia • Utilizzo più consapevole e significativo Osservazione dei concetti matematici nei tempi di ricreazione Osservazione dei concetti matematici nei tempi di ricreazione
- 23. ConclusioniConclusioni La recensione diun’alunna … piace di più la matematica perché spiegata facile è facile …
- 24. Le prime manifestazionistoriche
- 25. i modelli matematici •Con la modellistica si abbandona l’idea galileiana della semplicità della natura, che ebbe maggior sviluppo durante il ‘700 e inizio ‘800. • Agli inizi del ’900 ci si è resi conto che la linearizzazione conduceva ad errori. Lo sviluppo della modellistica matematica è legata allo sviluppo del paradigma della non linearità. La scienza e la tecnologia si rivolgono sempre più a sistemi complessi come i problemi del traffico o problemi legati alle file di attese. • Nasce l’esigenza dell’interazione di diverse competenze specifiche di diversi ambiti disciplinari come il biologo, lo psicologo, l’economista, il matematico, il programmatore È uno schema concettuale per rappresentare un insieme di fenomeni nel linguaggio matematico. Non è lo specchio di un fenomeno, né l’unica rappresentazione. Lo stesso modello può rappresentare più fenomeni in modo da scoprire aspetti comuni e i loro collegamenti (metodo dell’analogia)
- 26. Nella scuola primariaoggi I contenuti della matematica Aritmetica elementare Numeri e operazioni Misura Stima e calcolo di grandezza Geometria Figure geometriche, rappresentazione organizzazione dello spazio, simmetria e trasformazioni geometriche Dati e previsioni Trattamento dell’informazione quantitativa, statistica descrittiva e probabilità
- 27. Problemi È nella risoluzionedei problemi che la matematica esplica tutto il suo potenziale Valore potenzialmente pratico e utile per il futuro cittadino Formazione delle abilità euristiche – ricerca della verità ai quesiti posti Valore formativo: danno senso ai concetti matematici Nei semplici problemi della scuola primaria ritroviamo • La logica • L’ordine e il rigore • Il controllo e la verifica • La sollecitazione • Capire bene la domanda, i dati • Combinare i calcoli al ragionamento
- 28. George Polya Tratto dallaprefazione alla prima edizione “Un’idea geniale risolve spesso un grande problema, ma nella risoluzione di tutti i problemi interviene un pizzico di genialità. Può trattarsi di un problema modesto, ma se esso stuzzica la nostra curiosità ed eccita le nostre facoltà mentali e soprattutto se si riesce a risolvere da soli, si scoprirà l’ansia della ricerca e la gioia della scoperta. Simili esperienze, fatte a tempo opportuno … possono lasciare un’impronta nell’animo ...” Polya G., Come risolvere i problemi di matematica. Logica ed euristica nel metodo matematico. Feltrinelli, Milano, 1967
- 29. George Polya Tratto dallaprefazione alla prima edizione “… un insegnante di matematica ha una grande possibilità. Ovviamente se egli impiegherà le sue ore di lezione a far eseguire dei calcoli ai suoi studenti, finirà per soffocare il loro interesse, arrestare il loro sviluppo mentale e sciupare l’opportunità che gli si presenta. Invece se risveglierà la curiosità degli alunni proponendo problemi di difficoltà proporzionate alle conoscenze della scolaresca e li aiuterà a risolvere le questioni proposte con domande opportune, egli saprà ispirare in loro il gusto di un ragionamento originale” Polya G., Come risolvere i problemi di matematica. Logica ed euristica nel metodo matematico. Feltrinelli, Milano, 1967
- 30. George Polya Tratto dallaprefazione alla seconda edizione “Mentre era in corso la stampa di questa seconda edizione, uscì uno studio (Educational Testing Service, Princeton, N.Y. Dal “Time” 18 giugno 1956) che sembra aver avanzato alcune osservazioni in proposito …. “la matematica gode dell’incerto onere di essere la materia meno popolare della carriera scolastica … I futuri insegnanti imparano a detestarla fin dalle prime classi elementari … E così essi ritornano alle scuole per insegnare ad una nuova generazione ad odiare la stessa materia ”.
- 31. George Polya • AffermaGeorge Polya : “Insegnare a risolvere i problemi significa anche educare la volontà. Proprio risolvendo i problemi che non siano troppo facili, lo studente impara a perseverare … e ad apprezzare i piccoli successi” Polya G., Come risolvere i problemi di matematica. Logica ed euristica nel metodo matematico. Feltrinelli, Milano, 1982, pag. 104
- 32. George Polya Scrive Polya:“Risolvere i problemi è una questione di abilità vera e propria come, permettetemi il paragone, nuotare. Qualunque abilità pratica può essere acquisita con l’imitazione e l’esercizio … Per imparare a risolvere i problemi è necessario osservare ed imitare come vi riescono le altre persone ed infine si riesce a risolvere i problemi risolvendoli … Lo studente dovrebbe desiderare di conoscere la soluzione … i problemi dovrebbero essere scelti con cura, né troppo difficile né troppo facili, semplici ed interessanti … presentati in una forma gradevole, piana e atta a risvegliare la curiosità dei giovani” Polya G., Come risolvere i problemi di matematica. Logica ed euristica nel metodo matematico. Feltrinelli, Milano, 1982, pagg. 24-27
- 33. George Polya LE 4FASI PER LA RISOLUZIONE DEI PROBLEMI 1. Fase: Comprensione del problema Quali sono i dati? Sai porre il problema con le tue parole? Disegna una figura o uno schema 1. Fase: Compilazione o elaborazione di un piano Esiste un problema analogo che hai già risolto? Puoi risolvere un problema più semplice connesso a questo? Puoi suddividere il problema in più parti? 1. Sviluppo del piano, metterlo in pratica Procedi con pazienza e precisione. Sei capace di spiegare il tuo piano e come lo hai attuato? • Verifica Esaminare la soluzione ottenuta. Se non è verosimile forse hai fatto qualche errore? Puoi confrontare il tuo piano con altri? Fonti: Polya G., op. cit. pagg. 11-13 Millan Gasca A., Lezione 7: Risolvere problemi, Roma 2008/9, pag. 11