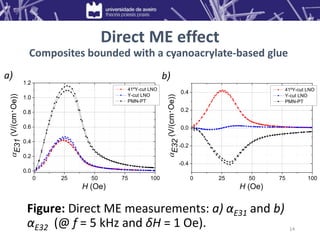
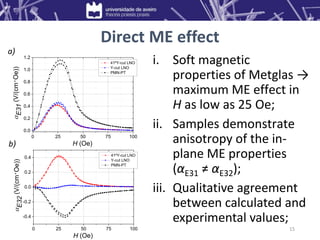
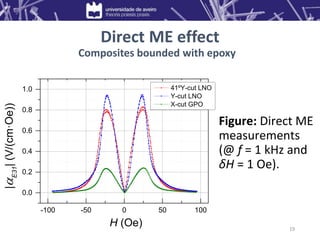
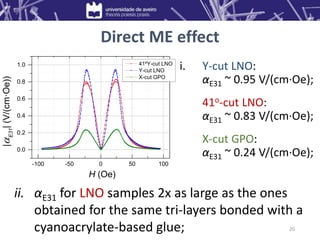
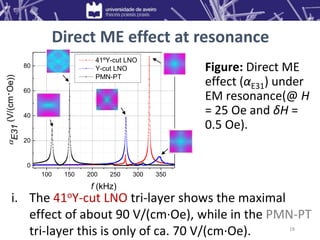
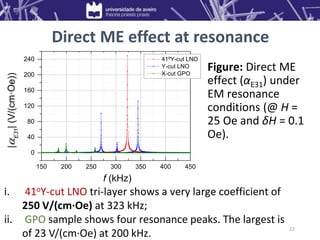
This document summarizes research on tri-layered magnetoelectric composites containing Metglas and various piezoelectric crystals. Key findings include: 1) Composites of Metglas/lithium niobate (LNO) and Metglas/gallium phosphate (GPO) exhibited direct magnetoelectric voltage coefficients of up to 0.95 V/(cm·Oe) and 0.24 V/(cm·Oe), respectively. 2) Under electromechanical resonance, the Metglas/LNO composite showed a very large coefficient of 250 V/(cm·Oe), while the Metglas/GPO composite showed a maximum of 23 V/(

1. Magnetoelectric Effect in tri-layered
composites of Metglas, LiNbO3,
GaPO4 and PMN-PT
João Vidal1, Andrey Timopheev1 , Andrei Kholkin2 and
Nikolai Sobolev1
1 Department of Physics & I3N, University of Aveiro, 3810-193
Aveiro, Portugal
2 Department of Materials and Ceramic Engineering & CICECO,
University of Aveiro, 3810-193 Aveiro, Portugal 1

2. Introduction
The linear Magnetoelectric (ME) effect
o Direct ME effect (MEH): o Converse ME effect (MEE):
• Induction of a
polarization, P, by
an applied
magnetic field, H.
• Induction of a
magnetization, M,
by an applied
electric field, E.
*αij (s/m) - linear ME susceptibility tensor. 2

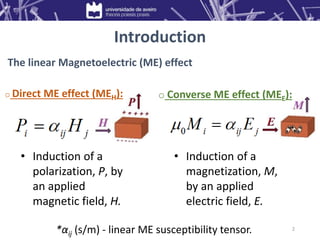
3. Introduction
• DC and AC magnetic field sensors;
• Electric current sensors;
• Multiple-state memories;
• RAM memories;
• Transformers;
• Read-heads;
• Diodes;
• Spin wave generators;
• Electrically tunable
microwave devices.
Applications
• Single-phase (multiferroics) • Composites
ME materials
• Intrinsic ME effect;
• Too small for any
practical application;
• Only at very low
temperatures.
• Incorporate both
ferroelectric (FE) and
ferri/ferromagnetic
(FM) compounds;
• Can exhibit large ME
effects at RT.
[W. Eerenstein et al.,
Nature 442 (2006)]
3

4. Introduction
Figure: ME effect
mediated by the elastic
coupling:
a) Direct effect;
b) Converse effect.
ME composites
Figure: Different
connectivity types.
4

5. Introduction
Past research on ME composites has been mostly focused
on FEs with large piezoelectric (d) and dielectric (ε)
coefficients such as PZT or PMN-PT.
ME composites
• Low Curie and depolarization temperatures (ca. 100oC);
• Toxicity of lead;
• Chemical and electrical instabilities;
• Non-linear behavior;
• Uneasy growth of high-quality PMN-PT crystals;
• Very high price.
Disadvantages
5

6. Introduction
MEH 𝑒𝑓𝑓𝑒𝑐𝑡 =
𝐸𝑙𝑒𝑐𝑡𝑟𝑖𝑐𝑎𝑙
𝑀𝑒𝑐ℎ𝑎𝑛𝑖𝑐𝑎𝑙
×
𝑀𝑒𝑐ℎ𝑎𝑛𝑖𝑐𝑎𝑙
𝑀𝑎𝑔𝑛𝑒𝑡𝑖𝑐
;
αij = kc(∂Pi/∂Hj ) = kc(∂Pi/∂Sk)(∂Sk/∂Hj) = kcdikqjk;
Since the measurable direct ME voltage coefficient (αEij ) is
proportional to the ratio between d and ε:
αEij = ∂Ei/∂Hj = αij/εij, (V/(cm·Oe))
alternative lead-free FEs also expected to exhibit large αEij in
composites.
ME composites
Piezoelectricity Magnetostriction
6

7. Properties of piezoelectric materials
BaTiO3 LiNbO3 GaPO4 PZT-5 PZT-4 PZN-PT PMN-PT PVDF NKN
𝒅𝟑𝟏
(pC/N)
–90 –0.85 -1.58 (𝒅𝟏𝟒) –175 –109 –1280 ≈ 700 16.5 -
𝒅𝟑𝟑
(pC/N)
191 6 4.37 (𝒅𝟏𝟏) 400 300 2000-2500 2000 –33 158
𝜺𝒓𝟑𝟑 1700 28.7 5.8 1750 1350 7200 5000 10 -
𝑻𝒄 (oC) 152 ≈ 1150 ≈ 933 360 320 163 80 129 415
𝝆 (g/cm3) 6 4.65 3.57 7.7 7.6 8.2 7.8 1.78 -
𝑸𝒎 - - - 80 500 - - 4 234
𝒌𝟑𝟑 0.63 - - 0.72 0.68 0.94 ≈ 0.9-0.94 0.19 0.46
d31 and d33 - piezoelectric strain coefficients; εr33 - relative dielectric permittivity; Tc/d
- Curie or depolarization temperature; ρ - mass density, Qm - mechanical quality
factor; k33 - electromechanical coupling factor. 7

8. Properties of magnetostrictive materials
NiFe2O4 Terfenol–D Galfenol Metglas 2605
𝝀𝒔 (ppm) 27 1400 200 40
𝒒𝟑𝟑
(ppm/Oe)
≈ 0.18 ≈ 1-2 ≈ 1.5 ≈ 4.0
𝝁𝒓𝟑𝟑 20 ≈ 6-10 20 > 40,000
𝑻𝒄 (oC) 535 380 - -
𝝆 (g/cm3) 5.37 7.8 7.7 7.18
𝝆′ (Ω.m) 1 x 106 5.8 x 10–7 6 x 10–7 1.3 x 10–6
λs - saturation magnetostriction; μr33 - relative magnetic permeability; ρ - mass
density; ρ‘ - electrical resistivity; TC - Curie temperature; q33 - piezomagnetic
coefficient.
8

9. Introduction
We report the possibility of generating relatively
large direct αEij of up to ca. 250 V/(cm·Oe) and
23 V/(cm·Oe) in tri-laminated systems containing
Metglas and crystalline LiNbO3 (LNO) and GaPO4
(GPO), respectively, under electromechanical
(EM) resonance conditions.
9
a) b)
Figure: Trigonal
structures of:
a) LNO (3m);
b) GPO (32).

10. Preliminary calculations
Estimation of the maximum expected transversal αE3a
for perfectly coupled ME tri-layered composites of
Metglas/Piezocrystal/Metglas by means of an
averaging quasi-static method*.
*H.-Y. Kuo et al., Smart Mater. Struct. 19 (2010). 10
Figure:
a) Tri-layered ME
composite operating
in the L-T mode.
b) Euler angles used in
the rotation of the
crystallographic
frame of the
piezocrystal.

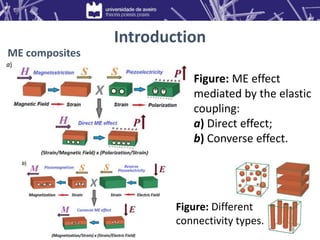
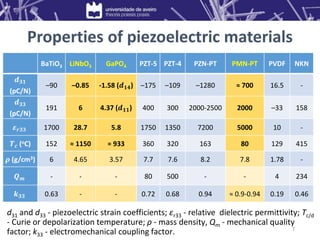
11. Preliminary calculations
 (deg)

(deg)
LiNbO3 Maximum |E| (V/cm-Oe)
0 20 40 60 80 100 120 140 160 180
0
20
40
60
80
100
120
140
160
180
5
10
15
20
25
 (deg)

(deg)
GaPO4 Maximum |E| (V/cm-Oe)
0 20 40 60 80 100 120 140 160 180
0
20
40
60
80
100
120
140
160
180
5
10
15
20
25
30
35
Piezoelectric
crystal
Maximum
|𝛼𝐸3𝑎|
(V/(cm·Oe))
Crystal cut
LNO 27.2 (ZXl) 39o
α–GPO 35.6 (XYt) 12o
PMN–31%PT
([011]-poled)
23.2 Z
Conclusion: Selection of
crystals with an appropriate
cut → very important step in
the development of good
ME composites.
Table: maximum expected
direct ME voltage coefficients.
LNO
GPO
11

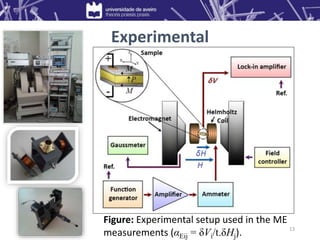
12.  Metglas/Piezocrystal/Metglas tri-layered composites
prepared:
Piezocrystals: Y-, 41oY-cut LNO and [011]-poled PMN-PT;
Bounding method: Cyanoacrylate-based glue;
Piezocrystals: Y-, 41oY-cut LNO and X-cut GPO;
Bounding method: Epoxy resin.
 ME properties studied:
• Impedance spectroscopy performed using a simple I-V
equivalent circuit;
• Direct ME effects measured by a dynamic lock-in technique
using a home-made setup.
Experimental
12

13. Figure: Experimental setup used in the ME
measurements (αEij = δVi/t.δHj).
Experimental
13

14. Direct ME effect
Figure: Direct ME measurements: a) αE31 and b)
αE32 (@ f = 5 kHz and δH = 1 Oe).
Composites bounded with a cyanoacrylate-based glue
14
0 25 50 75 100
0.0
0.2
0.4
0.6
0.8
1.0
1.2
41ºY-cut LNO
Y-cut LNO
PMN-PT
H (Oe)

E31
(V/(cm
·
Oe))
a)
0 25 50 75 100
-0.4
-0.2
0.0
0.2
0.4 41ºY-cut LNO
Y-cut LNO
PMN-PT
H (Oe)

E32
(V/(cm
·
Oe))
b)

15. Direct ME effect
i. Soft magnetic
properties of Metglas →
maximum ME effect in
H as low as 25 Oe;
ii. Samples demonstrate
anisotropy of the in-
plane ME properties
(αE31 ≠ αE32);
iii. Qualitative agreement
between calculated and
experimental values;
15
0 25 50 75 100
0.0
0.2
0.4
0.6
0.8
1.0
1.2
41ºY-cut LNO
Y-cut LNO
PMN-PT
H (Oe)

E31
(V/(cm
·
Oe))
a)
0 25 50 75 100
-0.4
-0.2
0.0
0.2
0.4 41ºY-cut LNO
Y-cut LNO
PMN-PT
H (Oe)

E32
(V/(cm
·
Oe))
b)

16. Direct ME effect
iv. αE3a one order of magnitude smaller than
expected → far from optimal elastic coupling
between phases;
v. Maximum αE31 of 1.15 V/(cm·Oe) in PMN-PT
sample → only ca. 3x larger than 0.47 and
0.42 V/(cm·Oe) in Y-cut and 41oY-cut LNO
samples.
Conclusion: The 3x greater αE3a of PMN-PT hardly
justifies an order of magnitude higher price and
an order of magnitude lower Curie temperature.
16

17. Impedance spectroscopy
50 100 150
0.01
0.1
1
10 2)
1) PMN-PT
Sim.
b)
|Y|
(mS)
f (kHz)
Figure:
Experimental and
simulated (using a
two dimensional
finite element
method)
impedance
spectra of: a) LNO
and b) PMN-PT
piezoelectric
crystals.
250 300 350 400
1E-3
0.01
0.1
1
4)
3)
2)
1)
Y-cut
Sim. Y
41ºY-cut
Sim. 41ºY
|Y|
(mS)
f (MHz)
a)
17

18. Direct ME effect at resonance
Figure: Direct ME
effect (αE31) under
EM resonance(@ H
= 25 Oe and δH =
0.5 Oe).
i. The 41oY-cut LNO tri-layer shows the maximal
effect of about 90 V/(cm·Oe), while in the PMN-PT
tri-layer this is only of ca. 70 V/(cm·Oe). 18
100 150 200 250 300 350
0
20
40
60
80

E31
(V/(cm
·
Oe))
41ºY-cut LNO
Y-cut LNO
PMN-PT
f (kHz)

19. Direct ME effect
Composites bounded with epoxy
Figure: Direct ME
measurements
(@ f = 1 kHz and
δH = 1 Oe).
19
-100 -50 0 50 100
0.0
0.2
0.4
0.6
0.8
1.0 41ºY-cut LNO
Y-cut LNO
X-cut GPO
|

E31
|
(V/(cm·Oe))
H (Oe)

20. Direct ME effect
i. Y-cut LNO:
αE31 ~ 0.95 V/(cm·Oe);
41o-cut LNO:
αE31 ~ 0.83 V/(cm·Oe);
X-cut GPO:
αE31 ~ 0.24 V/(cm·Oe);
ii. αE31 for LNO samples 2x as large as the ones
obtained for the same tri-layers bonded with a
cyanoacrylate-based glue; 20
-100 -50 0 50 100
0.0
0.2
0.4
0.6
0.8
1.0 41ºY-cut LNO
Y-cut LNO
X-cut GPO
|

E31
|
(V/(cm·Oe))
H (Oe)

21. Direct ME effect
iii. Almost complete absence of hysteretic
response → linear piezoelectric
properties of both LNO and GPO;
iv. 3x larger coefficient was expected for the
X-cut GPO sample, in relation to the Y-cut
LNO one → discrepancy between
piezoelectric/dielectric coefficients in
literature and the actual properties of
commercial GPO crystals.
21

22. Direct ME effect at resonance
Figure: Direct ME
effect (αE31) under
EM resonance
conditions (@ H =
25 Oe and δH = 0.1
Oe).
i. 41oY-cut LNO tri-layer shows a very large coefficient of
250 V/(cm·Oe) at 323 kHz;
ii. GPO sample shows four resonance peaks. The largest is
of 23 V/(cm·Oe) at 200 kHz.
22
150 200 250 300 350 400 450
0
40
80
120
160
200
240 41ºY-cut LNO
Y-cut LNO
X-cut GPO
|

E31
|
(V/(cm·Oe))
f (kHz)

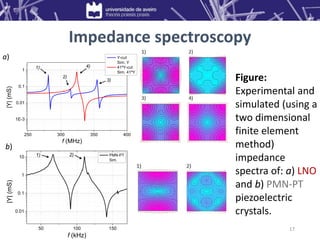
23. 23
Composite
Crystal
dimensions
(mm3)
Quasi-static
|αE3a|
(V/(cm·Oe))
EM resonance
|αE3a|
(V/(cm·Oe))
Ref.
M / 41oY-cut LNO / M 10 x 10 x 0.5 0.8 @ 25 Oe 250 @ 323 kHz -
M / X-cut GPO / M 10 x 10 x 0.5 0.2 @ 25 Oe 23 @ 200 kHz -
M / [011]-poled PMN-PT / M 10 x 10 x 0.5 1.2 @ 27 Oe 70 @ 150 kHz -
P / X-cut Quartz / P 45 x 5 x 0.5 4.8 @ 30 Oe 175 @ 58 kHz [1]
P / X-cut LGT / P 25 x 4.5 x 0.4 6.3 @ 40 Oe 155 @ 80 kHz [2]
P / PZT / P 25 x 4.5 x 0.4 0.6 @ 90 Oe 110 @ 90 kHz [2]
P / [001]-poled PMN-PT / P 20 x 5 x 0.3 1.3 @ 180 Oe 70 @ 115 kHz [2]
Direct ME effect
Table: Summary of the ME properties in some tri-layered composites.
FM alloys: Metglas (M); Permendur (P).
[1] G. Sreenivasulu et al., Phys. Rev. B 86(21), 214405 (2012);
[2] G. Sreenivasulu et al., Appl. Phys. Lett. 100(5), 052901 (2012).

24. Conclusions
•The direct ME effects exhibit
comparable magnitudes in layered
composites containing LNO, GPO and
PMN-PT crystals;
•A very large direct ME coefficient of
ca. 250 V/(cm·Oe) has been obtained
on the 41oY-cut LNO sample under
EM resonance;
24

25. Conclusions
• The EM resonances are situated in a very
suitable frequency range. As possible
applications, a full implementation could be
done using standard low-cost electronic
components (e.g. magnetic sensor based on a
crystal oscillator employing a ME composite as
resonator);
25
-100 -50 0 50 100
257.0
257.5
258.0
258.5
E31
E32
Res.
Frequency
(kHz)
H (Oe)
Figure: Resonance
frequency vs H in
ME M/GPO/M
crystal oscillator
sensor.

26. •The use of piezoelectric crystals with
different cuts should also allow one
to engineer desired anisotropic
properties;
•Crystalline LNO and GPO were
identified as strong candidates to
form their own field of ME-based
lead-free, linear, low-cost, high-
temperature magnetic-field sensors.
26
Conclusions

27. 27
Future work
• Further optimization of the relative
thickness of the layers and a better
mechanical coupling between them is
expected to enhance the ME effect by up
to an order of magnitude.
• In future this could be achieved by a direct
deposition of FM alloys on the
piezocrystals using thin-film technology
which would also open the way to the
miniaturization of such composites.

28. Thank you for your
attention
28