Laporan ini membahas percobaan pengolahan sinyal digital yang meliputi sinyal waktu kontinu dan diskrit, operasi dasar terhadap sinyal, dan penyelesaian persamaan beda rekursif menggunakan program M-file. Tujuan praktikum ini adalah memahami konsep sinyal waktu diskrit dan kontinu beserta operasinya serta sistem waktu diskrit.

1. LAPORAN PRAKTIKUM PENGOLAHAN SINYAL DIGITAL
PRAKTIKUM I
DisusunOleh :
Evrynda Widyasari P.D.
1400022058
PRODI TEKNIK ELEKTRO
FAKULTAS TEKNOLOGI INDUSTRI
UNIVERSITAS AHMAD DAHLAN
YOGYAKARTA
2017

2. A. TUJUAN
1. Memahami sinyal waktu diskrit dan kontinyu.
2. Memahami operasi-operasi pada sinyal
3. Memahami system waktu diskrit.
B. DASAR TEORI
Sinyal waktu kontinu (continu time) adalah sinyal dengan variable
independen bernilai nyata (read). Sinyal waktu diskrit (diskrate time)
adalah sinyal dengan variable independen bernilai integer. Perhatikan dua
sinyal berikut ini :
x(t) =sin (t/6) x(n)={
0.8 𝑛
,𝑛≥0
0 ,𝑦𝑎𝑛𝑔_𝑙𝑎𝑖𝑛
}
Sinyal x(t) adalah sinyal waktu kontinyu. Sinyal x(n) adalah sinyal waktu
diskrit.
Operasi Dasar Terhadap Sinyal :
a. Shift; suatu sinyal dapat digeser waktunya dengan mengganti variable
n dengan n-k, dengan k adalah bilangan bulat yang menyatakan unit
waktu bergeseran. Jika k bernilai positif maka pergeseran akan
menghasilkan sinyal yang tertunda (delay). Dalam grafik hal ini
ditunjukan dengan menggeser kekanan sejauh k. jika k bernilai
negative maka sinyal akan lebih cepat sebesar |k| (digeser ke kiri
sebesar |k|).
b. Folding/Reflection; operasi ini mencermikan x(n) x(-n).
c. Addition; jumlah dua buah sinyal pada saat yang bersamaan adalah
sama dengan jumlah dari besar kedua sinyal pada saat tersebut.
y(n) =𝑥1(n) +𝑥2(n).
d. Product; operasi ini didefinisikan melalui persamaan berikut:
y(n) =𝑥1(n) *𝑥2(n).
e. Scaling; mengalikan besar suatu sinyal dengan suatu konstanta A
y(n) = Ax(n).
C. HASIL DAN PEMBAHASAN

3. 1. Kita ketikkan program seperti pada langkah percobaan ke 1, pada M-
file, dan berikut tampilannya setelah kita ketikkan :
Setelah kita debug pada command window keluar sebagai berikut :

4. Keluaran dari M-File sebagai berikut :
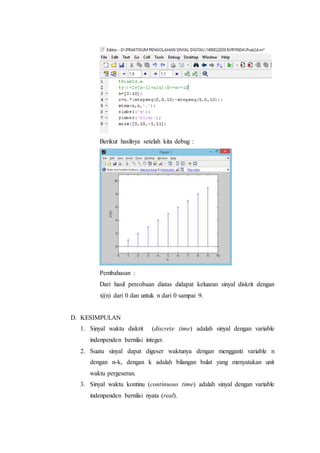
Pembahasan :
Dari hasil percobaan diatas kita ketahui bahwa hasil keluaran dari
sinyal kontinyu dari masukan pada M-file nilai x=e.-0.8t.sin (2/3t)
dengan matrik nilai [ 0 30 -1 1 ] dan nilai t memiliki rentang 0 sampai
30 dengan rasio 0.1 diatas, maka keluaranya adalah bentuk gelombang
sinusoida.Hasil keluaran dari sinyal Diskrit yang terbentuk dari
masukan pada M-file nilai x menujukan pada rentang -2 samapi 6
bernilai diskrit atau amplitudenya = [0 0 1 2 1 0 -1 0 0] .
2. Sistem pembayaran pinjaman Bank dapat dimodelkan sebagai sistem
waktu diskrit dengan persamaan beda sebagai berikut :
𝑦[ 𝑛] − (1 +
𝑎
12
) 𝑦[ 𝑛 − 1] = −𝑥[𝑛]
Dimana :
α : bunga pertahun
x[n] : jumlah angsuran per bulan
y[n] : sisa pinjaman setelah bulan ke-n
Untuk menentukan keluaraan y[n] dapat dilakukan perhitungan secara
rekursif sebagai berikut :

5. 𝑦[ 𝑛] = (1 +
𝑎
12
) 𝑦[ 𝑛 − 1] − 𝑥[𝑛]
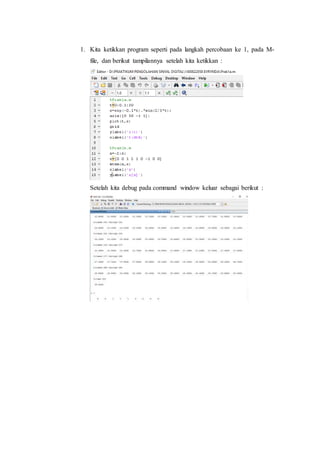
Pada M-File kita ketikkan program berikut ini :
Selanjutnya kita debug, berikut hasilnya saat angsuran perbulan 200:

6. Berikut perbandingan bila angsuran perbulan 300 :

7. Pembahasan :
Perbedaanya terlihat saat masukan angsuran perbulan 200 dan masukan
angsuran perbulan 300 nilai keluaran dari ans berbeda, angsuran 200
memiliki hasil akhir sampai=3.9857 sedangkan angsuran 300 memiliki hasil
akhir sampai=3.9170 .
3. Memodifikasi Program di atas, untuk menghitung penyimpanan uang
di bank, dengan bunga tiap kwartal yang dimodelkan dengan
persamaan beda berikut:
y[n]- 1+
𝑎
12
y[n-1]= -x[n].
Berikut kita ketikkan programnya di M-File :
Dengan a=10% , selanjutnya kita hitung y[n] untuk n=1.2.3.4 bila y[0]=1000 dan
x[n]=1000 untuk n≥1 .
Berikut hasilnya setelah kita debug dan kita masukkan seperti soal diatas :

8. Pembahasan :
Dari hasil percobaan diatas menghasilkan nilai c=1000 dan untuk hasil dari
0sampai 0.8333 tidak melebihi 1.
4. Pada M-File kita ketikkan program berikut ini :
Selanjutnya kita debug, maka akan menghasilkan figur berikut ini :
Pembahasan :
Dari hasil percobaan diatas didapat keluaran sinyal diskrit yang
bermulai dari x|(n) 0, dan n dari 0 sampai 9 dan berlanjut ke 0 sampai
seterusnya.
5. Buatlah program untuk menyelesaikan persamaan beda yang
berbentuk rekursif berikut, untuk 0≤n≤10
a. y[n]=0.5y[n-1]+u[n-1] y[-1]=0

9. Berikut programnya :
Selanjutnya kita debug, dan berikut hasilnya :
Pembahasan :
Dari hasil percobaan diatas didapat bahwa sinyal diskrit untuk x|(n)
dimulai dari 0 dan untuk n saro 0 sampai 4 lalu kembali ke 0
sampai seterusnya .

10. b. y[n]=2y[n-1]+u[n] y[-1]=1
Berikut programnya :
Selanjutnya kita debug, dan berikut hasilnya :
Pembahasan :
Dari hasil diatas didapat sinyal diskrit x|(n) dari 0 dan n dari 0
sampai 9
c. y[n]=0.5y[n-1]+0.1y[n-2]+u[n-1] ;y[-2]=1,y[-1]=0
Berikut programnya setelah kita ketikkan :

11. Berikut hasilnya setelah kita debug :
Pembahasan :
Dari hasil percobaan diatas didapat keluaran sinyal diskrit dengan
x|(n) dari 0 dan untuk n dari 0 sampai 9.
D. KESIMPULAN
1. Sinyal waktu diskrit (discrete time) adalah sinyal dengan variable
indenpenden bernilai integer.
2. Suatu sinyal dapat digeser waktunya dengan mengganti variable n
dengan n-k, dengan k adalah bilangan bulat yang menyatakan unit
waktu pergeseran.
3. Sinyal waktu kontinu (continuous time) adalah sinyal dengan variable
indenpenden bernilai nyata (real).

12. 4. Dari percobaan diatas juga merupakan kombinasi dari sinyal waktu
kontinyu dengan diskrit.
E. REFERENSI
Fadlil,Abdul.2017.Petunjuk Praktikum Pengolahan Sinyal Digital.
Yogyakarta : Universitas Ahmad Dahlan.