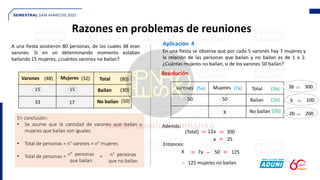
This document discusses ratios and their applications in arithmetic and geometry. It provides examples of using ratios to solve problems involving ages, mixtures, meetings, and mobile objects. Ratios can be expressed as comparisons using subtraction in arithmetic ratios or division in geometric ratios. The key points are that ratios of initial quantities are maintained even after amounts are added or removed, and time or distance ratios between objects will match their velocity or speed ratios. The document concludes with applications of ratios to word problems involving ages over time, mixing liquids with changing volumes, tracking attendees at events, and objects moving towards each other.

2. - RAZONES
- APLICACIÓN DE LAS RAZONES
ARITMÉTICA

3. Razón
En matemáticas, una razón
es la comparación de dos
cantidades.
Ésta comparación puede
realizarse por medio de la
sustracción o la división.
2 L 3 L
S/ 7.00 S/ 9.00

4. Razón Aritmética
Si las longitudes de los ríos Rímac y Chillón son 204 km y 126
km respectivamente. Halle la razón aritmética de sus
longitudes
Es la comparación de dos cantidades mediante la sustracción, en dicha comparación se determina en cuanto
excede una de las cantidades a la otra.
Ejemplo
204 126
− = 78
razón aritmética valor de la razón
aritmética
“La longitud del rio Rímac excede a la longitud
del rio Chillón en 78 km”
a b
− = r
antecedente consecuente valor de la razón
aritmética
En General

5. El puntaje obtenido por Alex
excede en 300 puntos al obtenido
por Beto; mientras que el puntaje
de Carlos es excedido por el de
Beto en 200 puntos. ¿Cuál es el
puntaje obtenido por Beto, si la
suma de puntajes de Alex y Carlos
es 2500?
Resolución
Aplicación 1
Sean:
• A: puntaje de Alex
• B: puntaje de Beto
• C: puntaje de Carlos
De los datos, tenemos que:
A B
− = 300
∴ Beto obtuvo 1200 puntos
2B
−
= 2400
A C
−
= 2500
A 300 +
= B
B C
− = 200 C B
= 200
Además, se sabe que:
+
( 300 + B ) + ( B 200 ) = 2500
B = 1200
Si P excede a Q en 12
unidades, tendremos:
P Q
− = 12
Si P es excedido por Q en 12
unidades, tendremos:
Q P
− = 12
Nota
Piden: Puntaje de Beto (B)

6. Razón Geométrica
Los precios de un medicamento comercial y genérico son
S/60 y S/20. Halle la razón geométrica de estos precios.
Es la comparación de dos cantidades mediante la división, en dicha comparación se determina cuantas veces
está contenido una cantidad en la otra.
Ejemplo
60
20
____ = 3
razón
geométrica
valor de la razón
geométrica
“El costo de un medicamento comercial es 3
veces el costo de un genérico”
antecedente
consecuente
a
b
____ = k
valor de la razón
geométrica
En General

7. Observaciones referentes a la razón geométrica
A es dos veces B, se expresa:
A = 2B
A es dos veces más que B, se expresa:
Observación 1
A = B + 2B
A = 3B
Observación 3
Si dos números A y B son entre como 7 es a 3, tendremos:
A
B
___ =
7
3
__ 14
6
21
9
A
B
. . .
. . .
7 k
3 k
x2
x2
x3
x3
Observación 2
De los dos tipos de razones, la que tiene mayor
aplicación es la razón geométrica. Entonces, si en
problema se indica la palabra razón, se entenderá
que hace referencia a la razón geométrica.

8. Aplicaciones
de las razones
Con el tema de razones
podemos resolver diversas
situaciones, como problemas
de edades, móviles,
reuniones, mezclas, etc.
A continuación detallaremos
algunas de ellas.

9. Razones en problemas de edades
Sandra y Valeria actualmente tienen 24 y 18 años
respectivamente. ¿Cuáles eran sus edades hace 4 años y
que edad tendrán dentro de 8 años?
Sandra
Valeria
Presente Futuro
Pasado
24
18
32
26
20
14
4 años 8 años
Diferencia de
edades
6 6
6
En conclusión, cuando comparemos las edades de dos
personas se deberá tener en cuenta que la diferencia de
las edades de estas es siempre la misma.
La diferencia de las edades
siempre es la misma
Aplicación 2
Las edades de José y Eduardo están en la relación de 7 a 3
respectivamente y dentro de 20 años sus edades estarán en la
relación de 3 a 2. ¿Cuál es la edad de José?
José
Eduardo
Presente Futuro
3b
2b
7a
3a
20 años
Diferencia de edades 4a 1b
iguales
De la tabla tenemos:
Toma el
valor de 5a
5a = 20
a = 4
∴ José tiene: 7 a = 28
Resolución
= 4a
= 8a
= 12a

10. Razones en problemas de mezcla
En conclusión, cuando tengamos una mezcla, los
volúmenes de los ingredientes que hay al inicio, en lo que
se extrae y en lo que queda siempre se encuentran en la
misma relación
Aplicación 3
De una mezcla de 70 L de agua y 30 L de alcohol, se extraen 40 L.
¿Cuánto de alcohol se le debe agregar a lo que queda de la mezcla,
para que la relación inicial de agua y alcohol se invierta?
Luego
En un recipiente se tiene una mezcla de 30 litros de agua
con 20 litros de vino. Si se extrae 15 litros de la mezcla,
¿cuánto de agua y vino quedará?
agua
vino
Inicio Extrae Queda
(3k)
(2a)
(3a)
(2k)
5k = 15
K= 3
9L
6L
21L
14L
(3b)
(2b)
15 L
Resolución
70L
30L
agua
alcohol
Inicio Extrae Queda
(7b)
(3a)
(7a)
(3b)
9L
40 L 60 L
42L
18 L
100 L
42
18 + x
_____ =
3
7
__
(14)
(14)
18 + x = 98
x = 80
∴ Se debe agregar 80 L de alcohol.
30L
20L
Se agrega x
litros de
alcohole
10b = 40
b= 4
12 L
28 L

11. Razones en problemas de reuniones
A una fiesta asistieron 80 personas, de los cuales 48 eran
varones. Si en un determinando momento estaban
bailando 15 mujeres, ¿cuántos varones no bailan?
Mujeres
Varones (32)
En conclusión:
• Se asume que la cantidad de varones que bailan y
mujeres que bailan son iguales
• Total de personas = n° varones + n° mujeres
• Total de personas = +
Aplicación 4
En una fiesta se observa que por cada 5 varones hay 7 mujeres y
la relación de las personas que bailan y no bailan es de 1 a 2.
¿Cuántas mujeres no bailan, si de los varones 50 bailan?
Resolución
Bailan
No bailan
(48)
(30)
15
(50)
33
15
17
Total (80)
n° personas
que bailan
n° personas
que no bailan
Mujeres
Varones (7a)
Bailan
No bailan
(5a)
(1b)
50
(2b)
50
X
Total
b = 100
(Total) = 12a = 300
a = 25
Entonces:
X = 7a − 50 = 125
∴ 125 mujeres no bailan.
Además:
(3b) 3b = 300
2b = 200

12. Razones en problemas de móviles
Dos móviles A y B parten simultáneamente a su encuentro
con velocidades de 20 km/h y 30 km/h. ¿En que relación
estarán las distancias recorridas después de t horas?
En conclusión, cuando el tiempo que transcurre sea igual
para ambos móviles, la relación de las velocidades será el
mismo que la relación de sus distancias recorridas.
Aplicación 5
Luis y Erick están separados cierta distancia y parten a su
encuentro con velocidades que están en la relación de 5 a 7. Si al
cabo de cierto tiempo aún están separados 500 m y hasta ese
momento Erick avanzó 140 m, ¿cuál es la separación inicial de las
personas?
Resolución
∴ La distancia inicial de separación es 740 m.
𝑉𝐴= 20 km/h 𝑉𝐵 = 30 km/h
t h t h
𝑑𝐴 = 20t 𝑑𝐵 = 30t
Donde:
___ =
2
3
__
𝑉𝐴
𝑉𝐵
___ =
2
3
__
𝑑𝐴
𝑑𝐵
𝑉𝐿 = 5a 𝑉𝐸 = 7a
140 m
500 m
Luis Erick
X m
𝑑𝐿
Donde:
___ =
5
7
__
𝑑𝐿
140 (20)
(20)
Entonces:
X = 100 + 500 + 140 = 740

13. w w w. aduni. edu. pe