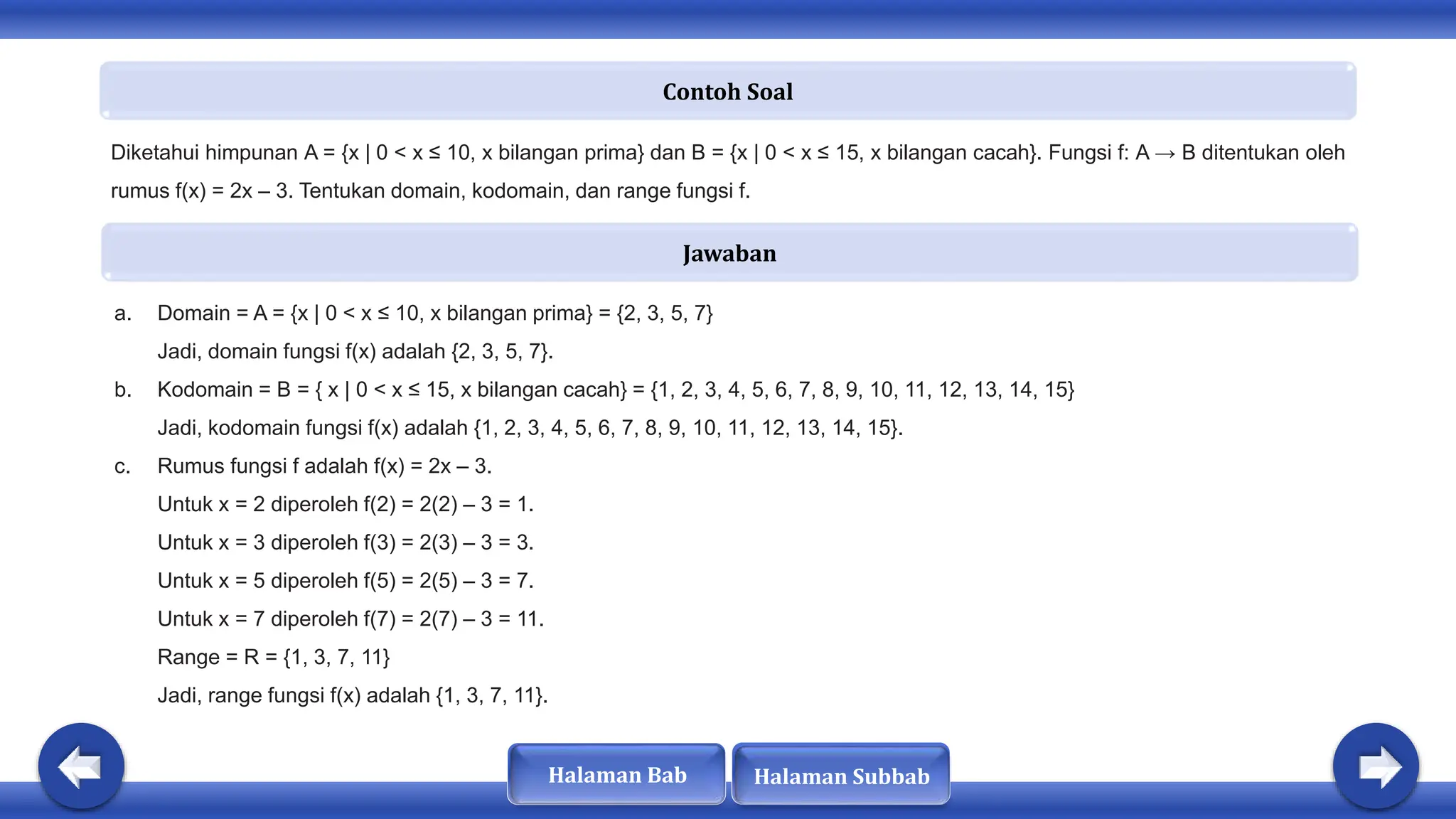
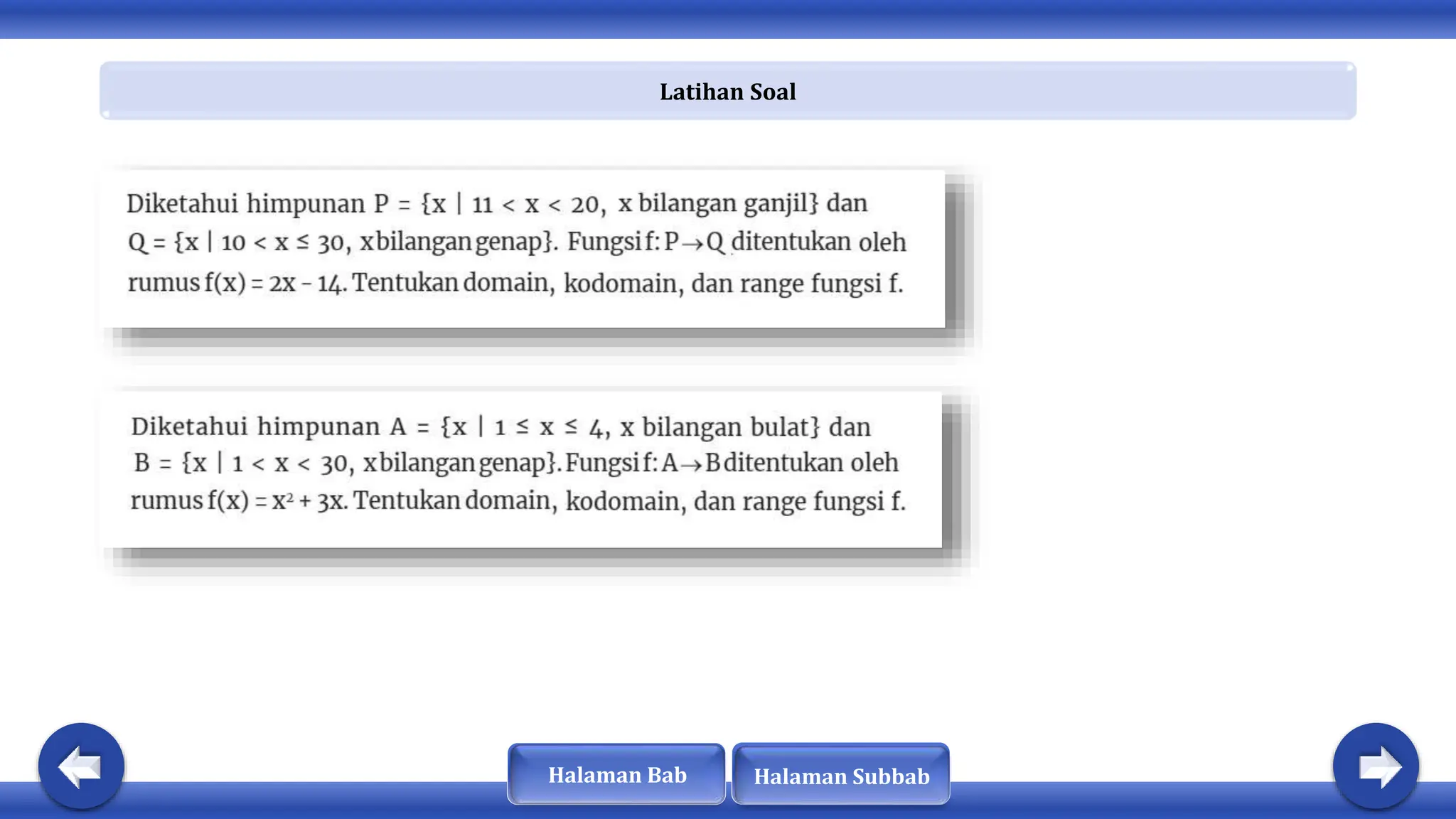
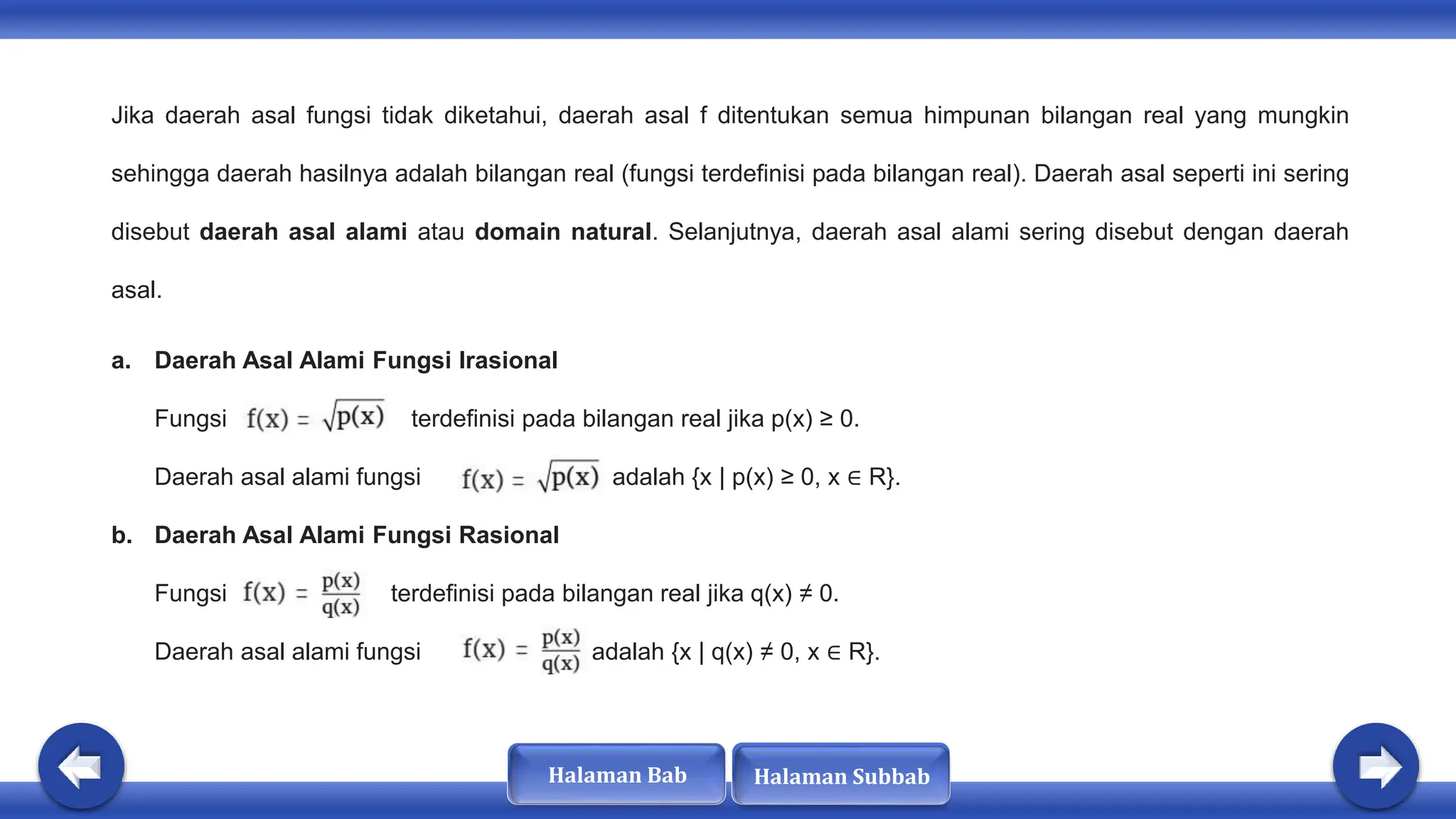
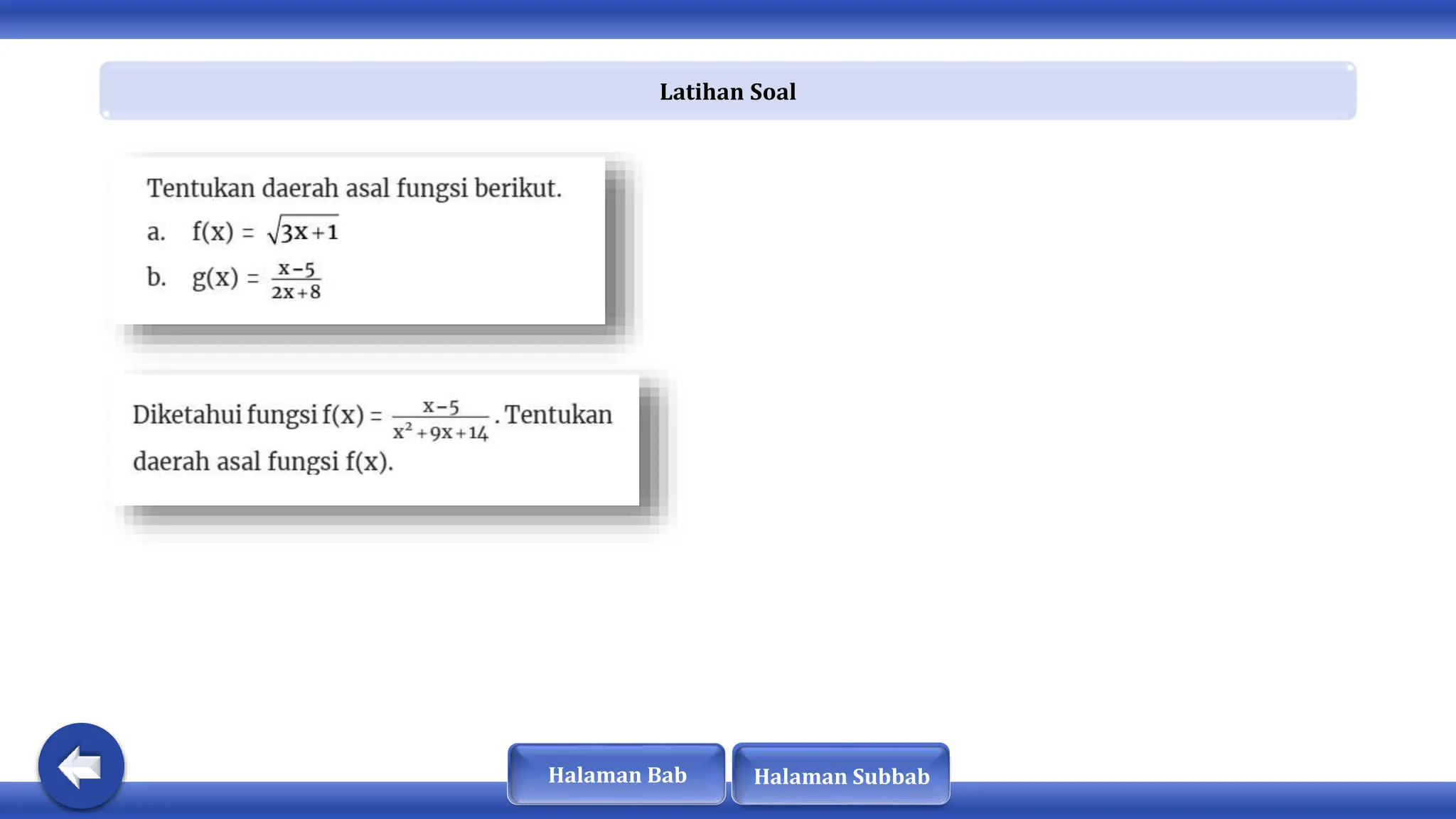
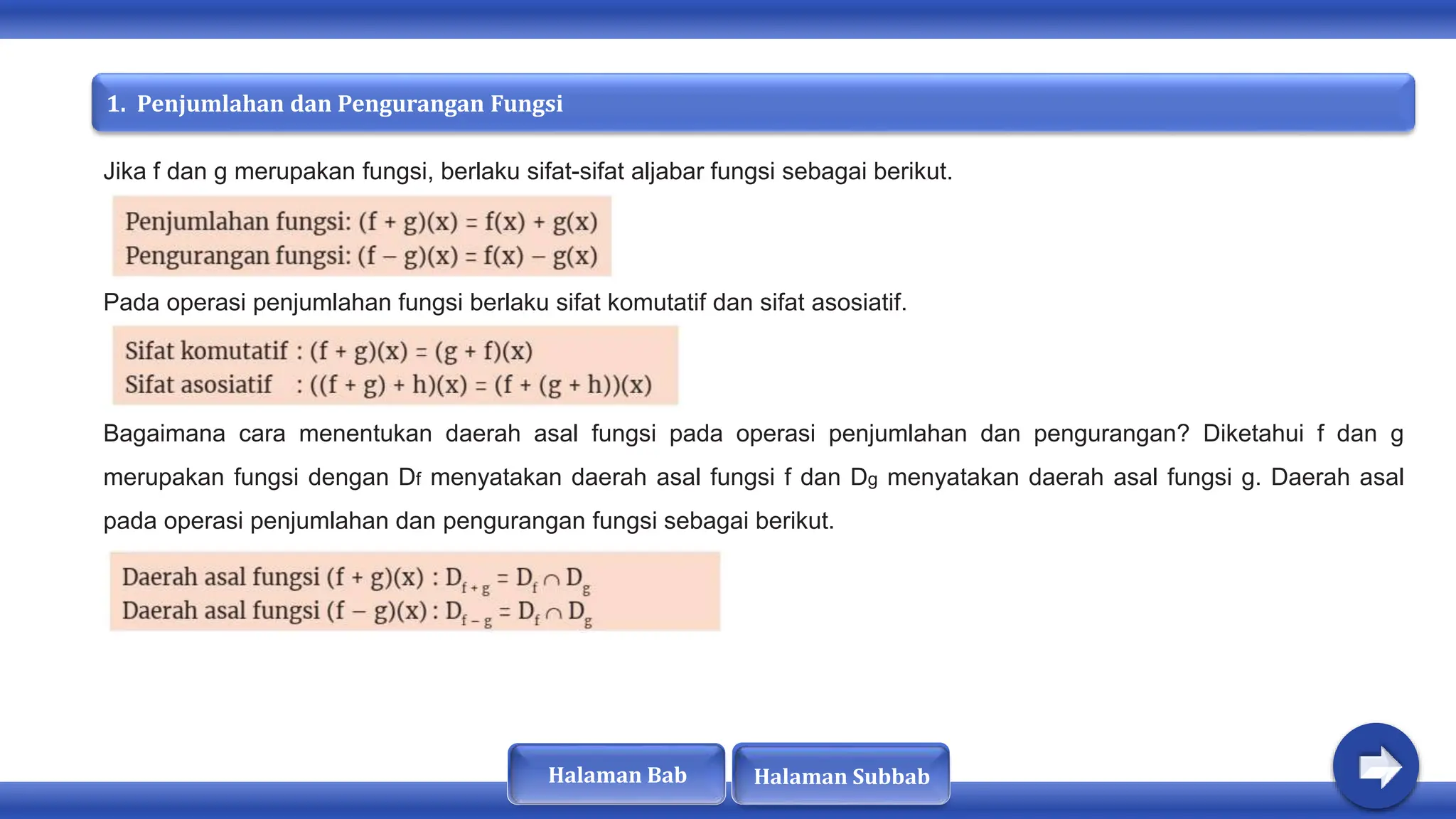
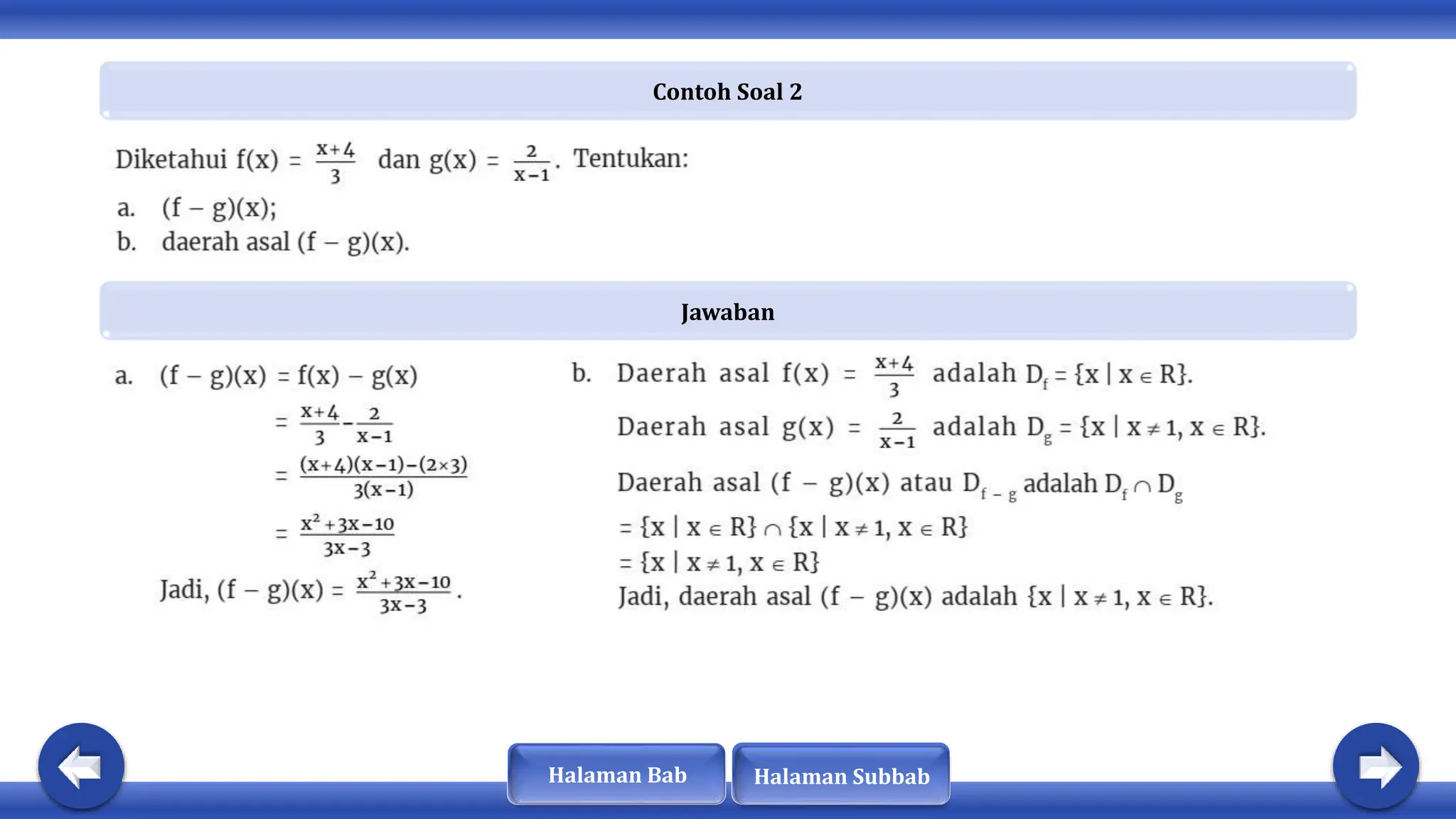
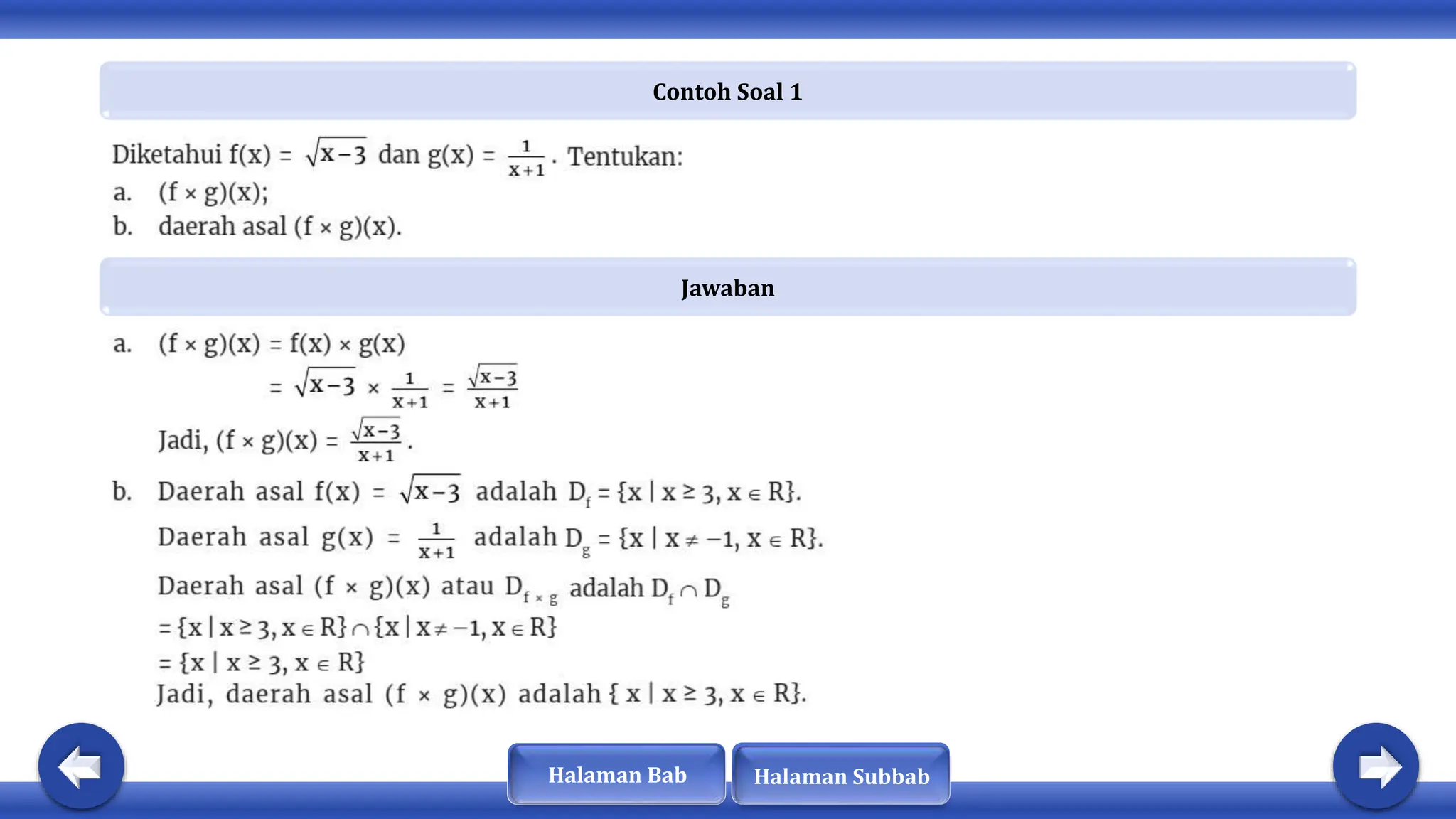
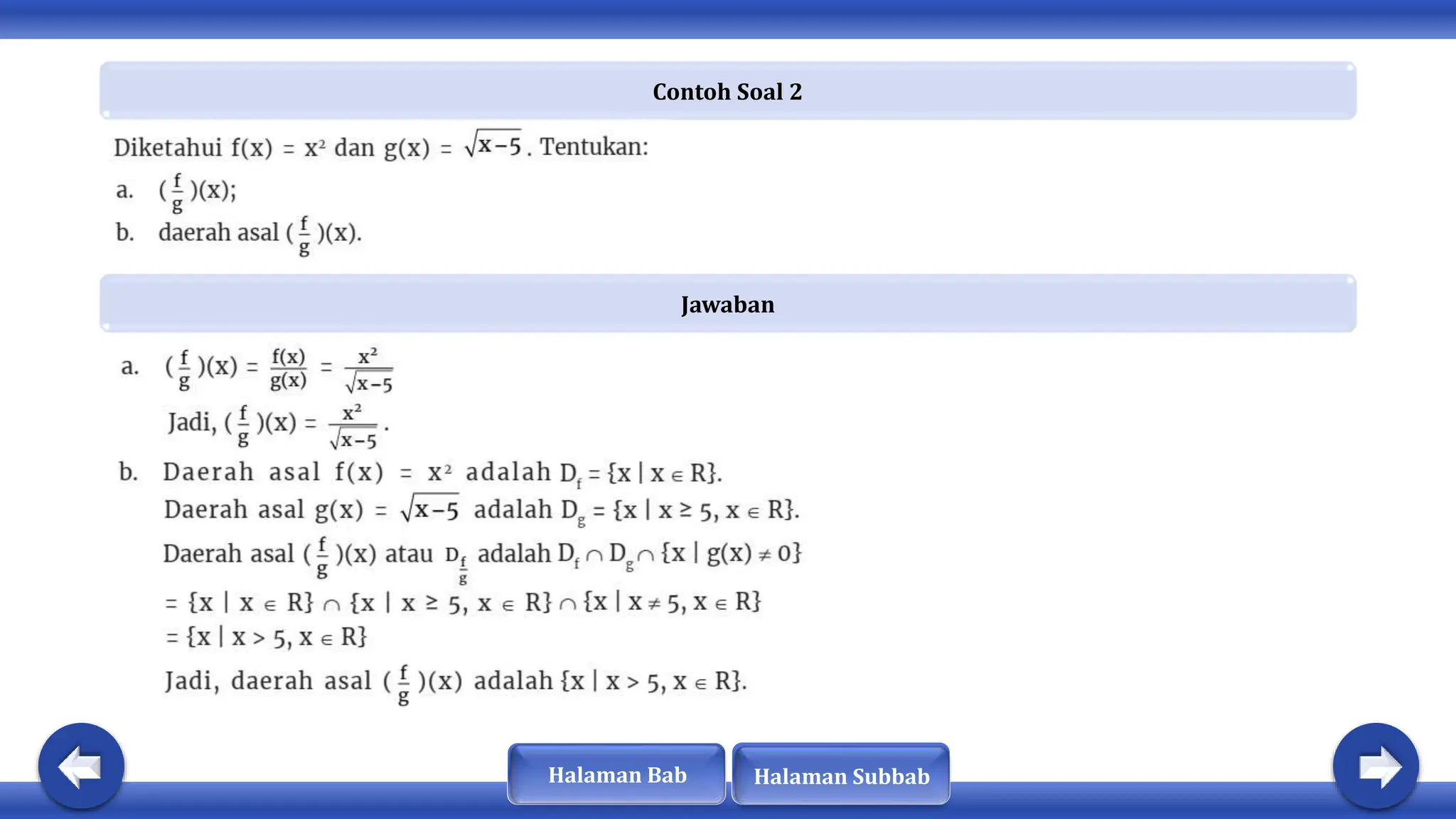
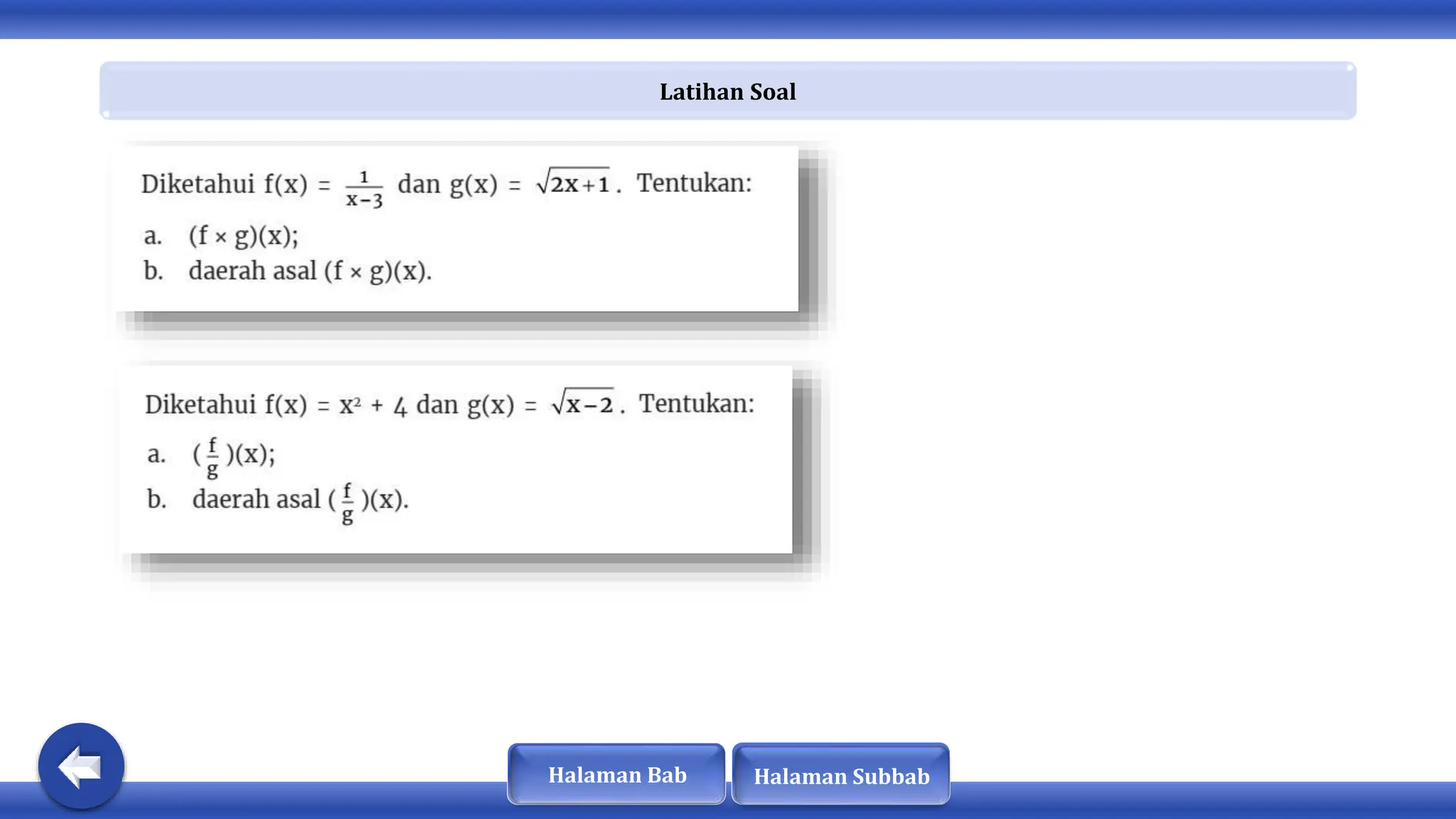
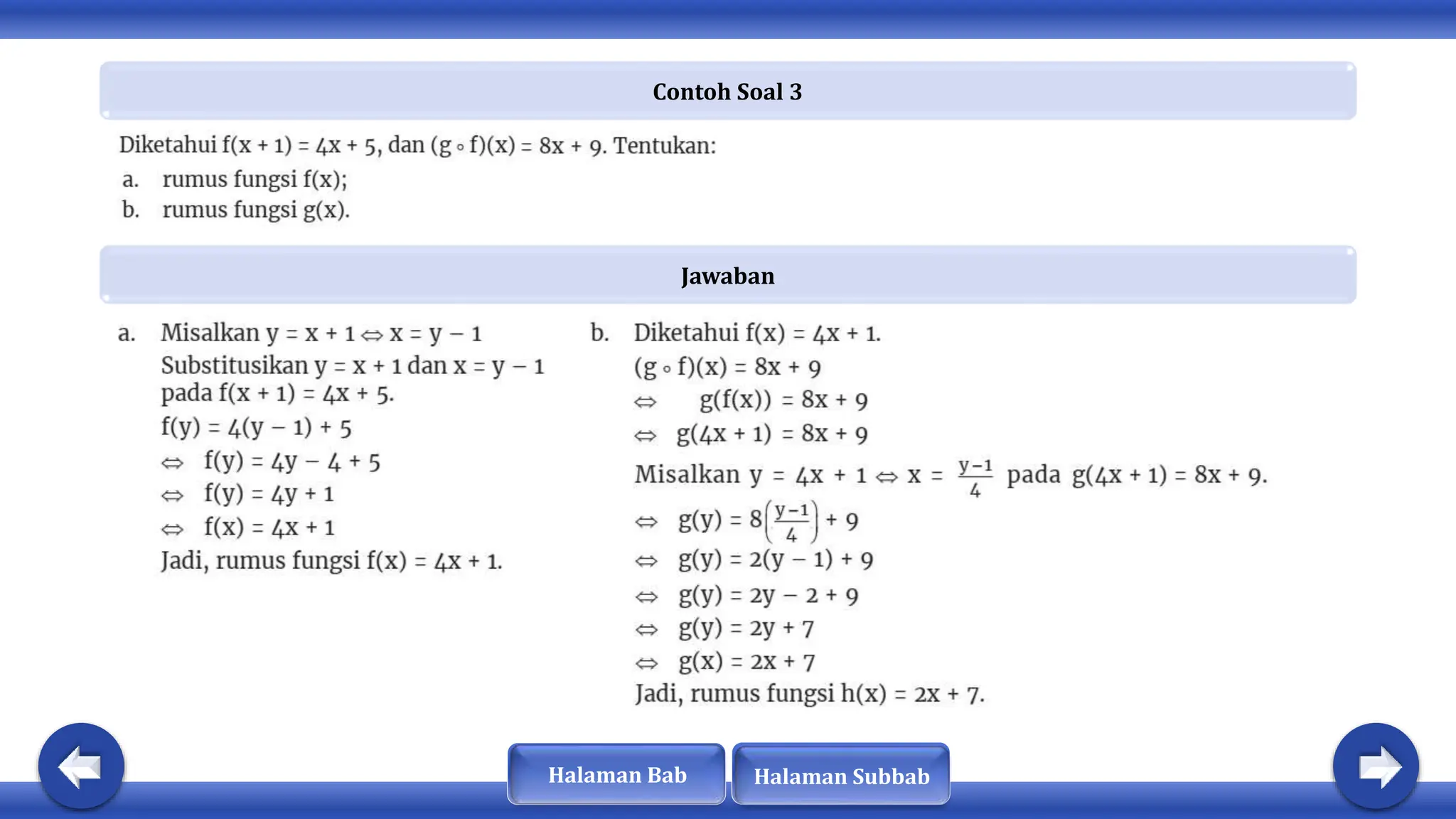
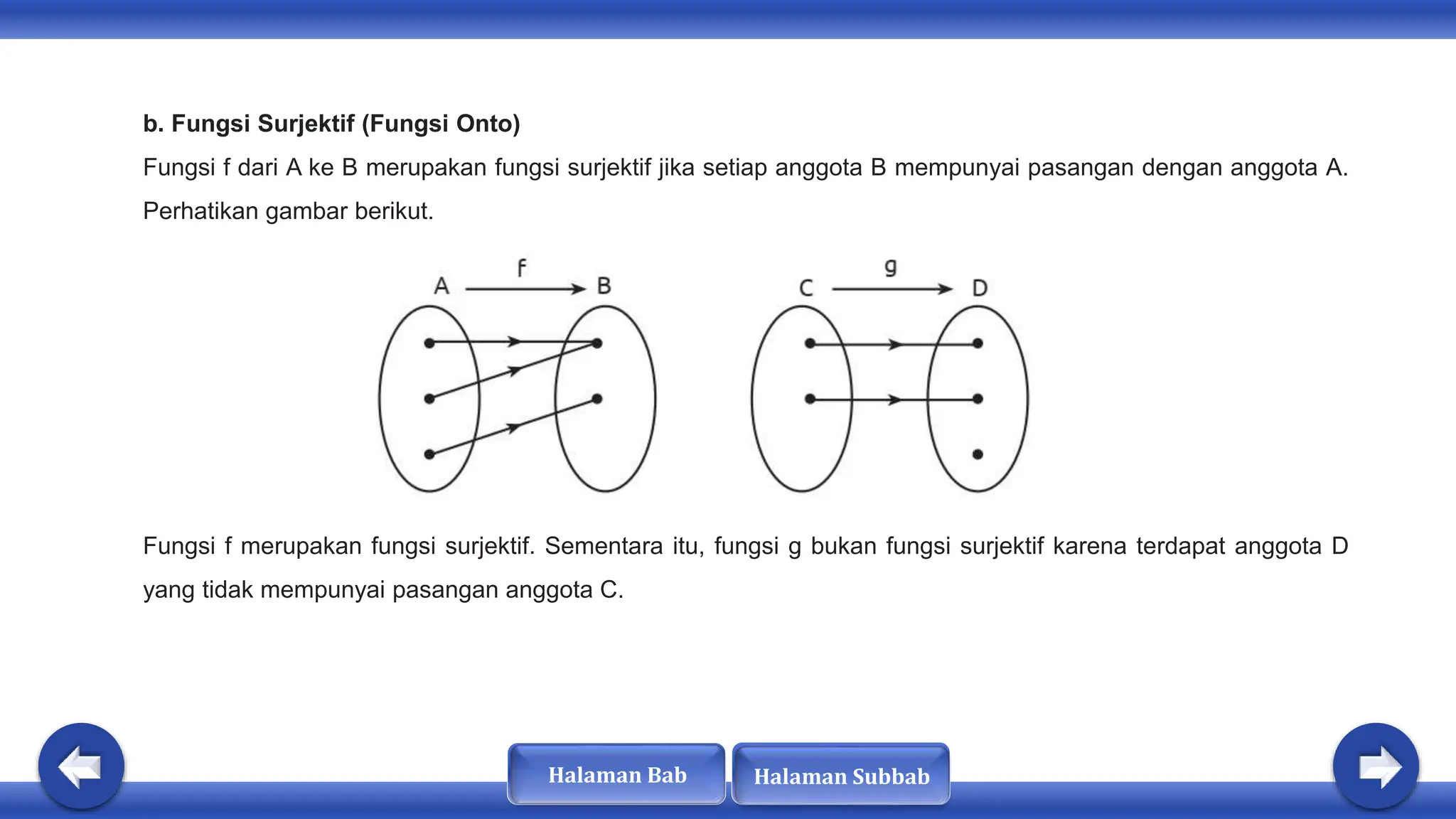
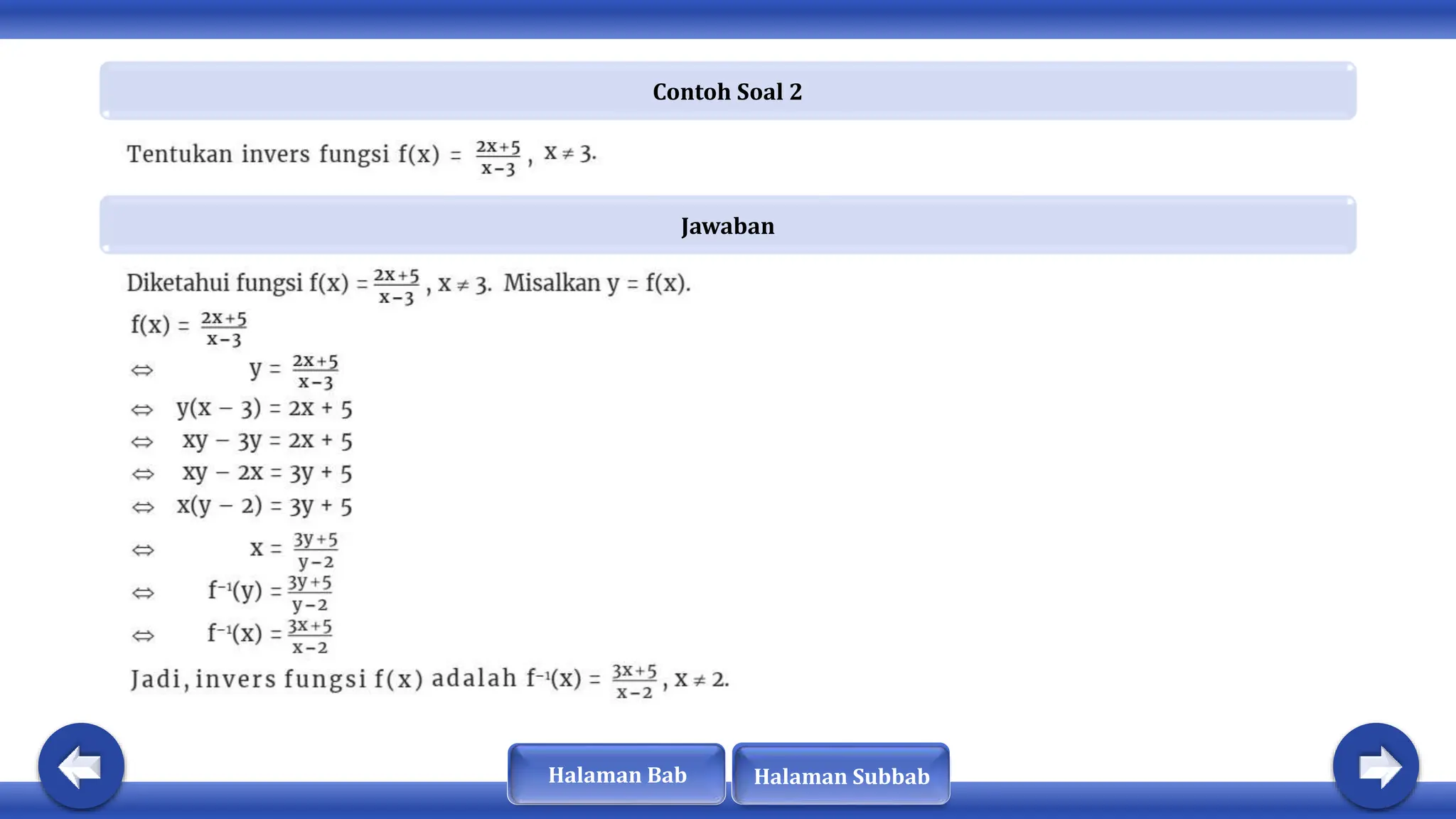
Dokumen ini membahas tentang konsep fungsi, komposisi fungsi, dan fungsi invers. Dinyatakan bahwa fungsi memiliki sifat khusus dan terdapat hubungan antara domain, kodomain, dan range. Selain itu, fungsi dapat diklasifikasikan sebagai injektif, surjektif, atau bijektif, dan hanya fungsi bijektif yang memiliki invers.