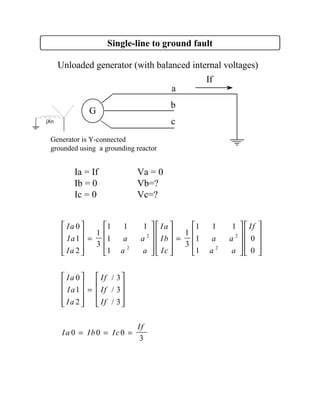
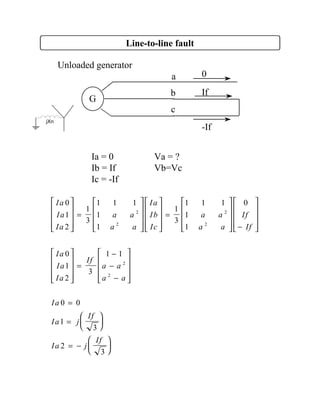
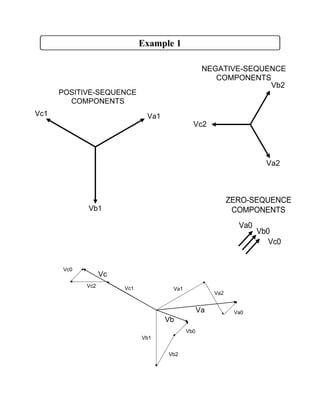
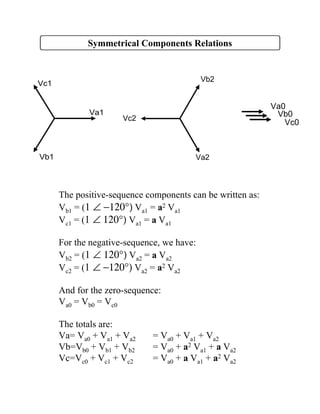
Symmetrical components decompose unbalanced three-phase systems into three balanced component systems - positive, negative, and zero sequences. The positive sequence components are balanced phasors equal in magnitude and displaced 120 degrees from each other with the same phase sequence as the original phasors. The negative sequence components are balanced but with the opposite phase sequence. The zero sequence components have equal phasors with zero phase displacement. The original phasors are the sum of their symmetrical components. Symmetrical components allow the analysis of faults in three-phase systems.

1. Symmetrical Components
à Fortescue’s Theorem
o 3 unbalanced phasors of a 3-phase system can be
resolved into 3 balanced systems of phasors.
The balanced sets of components are:
•Positive-sequence components
+ 3 balanced phasors
ð equal in magnitude
ð displaced from each other by 120°
ð same phase sequence as the original
phasors (for example a-b-c)
‚Negative-sequence components
− 3 balanced phasors
ð equal in magnitude
ð displaced from each other by 120°
ð opposite phase sequence to the
original phasors (for example a-c-b)
€Zero-sequence components
0 3 equal phasors
ð equal in magnitude
ð zero phase displacement from each
other

2. Symmetrical Components
Original voltages:
Va Vb Vc
Positive-sequence components:
Va1 Vb1 Vc1
or
Va+ Vb+ Vc+
Negative-sequence components:
Va2 Vb2 Vc2
or
Va- Vb- Vc-
Zero-sequence components:
Va0 Vb0 Vc0
ORIGINAL PHASORS ARE THE SUM OF THEIR
COMPONENTS:
Va = Va0 + Va1 + Va2
Vb = Vb0 + Vb1 + Vb2
Vc = Vc0 + Vc1 + Vc2

3. Example 1
Va1
Vb1
Vc1
POSITIVE-SEQUENCE
COMPONENTS
NEGATIVE-SEQUENCE
COMPONENTS
Va2
Vb2
Vc2
Va0
Vb0
Vc0
ZERO-SEQUENCE
COMPONENTS
Va1
Vb1
Vc1
Vc2
Vc0
Va2
Va0
Vb2
Vb0
Va
Vb
Vc

4. Example 2
Va1
Vb1
Vc1
Va2
Vb2
Vc2
Va0
Vb0
Vc0
Va
Vb
Vc

5. Example 3
Va1
Vb1
Vc1
Va2
Vb2
Vc2
Va0=Vb0=Vc0=0
Va=Vc
Vb

6. Operators
à Lets define a phasor:
a = 1 ∠ 120° = -0.5 + j 0.8666
The following relations are true:
a2 = (1∠120°)(1∠120°) = 1 ∠240°= 1 ∠ −120°
a3 = 1 ∠360°= 1 ∠ 0°
1 + a + a2 = 0
120°
a 3 = 1
a 2 = 1 -120
a = 1 120

7. Symmetrical Components Relations
Va1
Vc1
Vb1
The positive-sequence components can be written as:
Vb1 = (1 ∠ −120°) Va1 = a2 Va1
Vc1 = (1 ∠ 120°) Va1 = a Va1
For the negative-sequence, we have:
Vb2 = (1 ∠ 120°) Va2 = a Va2
Vc2 = (1 ∠ −120°) Va2 = a2 Va2
And for the zero-sequence:
Va0 = Vb0 = Vc0
The totals are:
Va= Va0 + Va1 + Va2 = Va0 + Va1 + Va2
Vb=Vb0 + Vb1 + Vb2 = Va0 + a2 Va1 + a Va2
Vc=Vc0 + Vc1 + Vc2 = Va0 + a Va1 + a2 Va2
Va2
Vb2
Vc2
Va0
Vb0
Vc0

8. Symmetrical Components Relations
I n m a t r i x f o r m :
V a
V b
V c
T h i s d e f i n e s t h e t r a n s f o r m a t i o n m a t r i x :
A =
I t s i n v e r s e i s :
A =
1
3
T h e r e f o r e :
V
V
V
1
3
- 1
a 0
a 1
a 2










=


















































=





1 1 1
1
1
1 1 1
1
1
1 1 1
1
1
1 1 1
1
1
2
2
0
1
2
2
2
2
2
2
2
a a
a a
V
V
V
a a
a a
a a
a a
a a
a a
a
a
a
( )
( )
( )















+ +
+ +
+ +
V a
V b
V c
V a V b V c
V a a V b a V c
V a a V b a V c
o r :
V =
1
3
V =
1
3
V =
1
3
a 0
a 1
a 2
2
2

9. Example
Ia=10 A.
Ib=-Ia
Ic=0
[ ]
[ ]
[ ]
Ia =10 0 A. Ib = 10 180 A. Ic = 0 A.
Ia0 =
1
3
10 0 10 180
Ia1=
1
3
10 0 10 180
Ia2 =
1
3
10 0 10 180
Ib0 = Ia0 = 0
Ib1=
Ib2 =
Ic0 = Ia0 = 0
Ic1=
∠ ° ∠ °
∠ °+ ∠ °+ =
∠ °+ ∠ ° ∠ ° + = ∠ − °
∠ °+ ∠ ° ∠ − ° + = ∠ °
∠ − °− °= ∠ − °
∠ + °+ °= ∠ + °
∠ − °+
0 0
1 120 0 578 30
1 120 0 578 30
578 30 120 578 150
578 30 120 578 150
578 30
( )( ) .
( )( ) .
. .
. .
. 120 578 90
578 30 120 578 90
°= ∠ + °
∠ + °− °= ∠ − °
.
. .
Ic2 =

10. Unloaded Generator
a
b
c
n
Ea
Eb
Ec
+
+
+
-
-
-
Internal voltages are balanced.
Find the symmetrical components for the internal voltages.
Ea0
Ea1
Ea2
Ea
Eb
Ec
Ea
Ea
Ea
Ea0
Ea1
Ea2
0
Ea
0










=




















=






























=










1
3
1 1 1
1
1
1
3
1 1 1
1
1
2
2
2
2
2
a a
a a
a a
a a
a
a
Only positive-sequence voltage exists!!!
jXn
Generator is grounded through a grounding reactor

11. Generator Equivalent
jX1
+
Ea1
-
Positive-sequence
jX2
Negative-sequence
jX0
j3Xn
Zero-sequence
Xn=Impedance from
neutral to ground
The current in the neutral of the generator is:
In = Ia + Ib + Ic = ( Ia1 + Ib1 + Ic1) + (Ia2 + Ib2 + Ic2 ) + Ia0 + Ib0 + Ic0
The positive and negative sequence components add to zero:
Ia1 + Ib1 + Ic1 = 0
Ia2 + Ib2 + Ic2 = 0
This means that the neutral does not carry positive or negative sequence
components.
However, the zero-sequence components are in phase, and their sum is:
In = Ia0 + Ib0 + Ic0 = 3 Ia0
Therefore the zero sequence equivalent has a grounding impedance of
value: Zg = 3 j Xn

12. Single-line to ground fault
Unloaded generator (with balanced internal voltages)
a
b
c
G
Generator is Y-connected
grounded using a grounding reactor
If
Ia = If Va = 0
Ib = 0 Vb=?
Ic = 0 Vc=?
Ia
Ia
Ia
a a
a a
Ia
Ib
Ic
a a
a a
If
Ia
Ia
Ia
If
If
If
Ia Ib Ic
If
0
1
2
1
3
1 1 1
1
1
1
3
1 1 1
1
1
0
0
0
1
2
3
3
3
0 0 0
3
2
2
2
2










=




















=






























=










= = =
/
/
/
jXn

13. Single-line to ground fault
jX1
+
Ea1
-
jX2
jX0
j3Xn
Ia1=Ia2=Ia0
Ia2
Ia0
+
Va = Va0 + Va1 + Va2 = 0
-
+
Va1
-
+
Va2
-
+
Va0
-
We have Ia1=Ia2=Ia0 and Va=0.
This situation can be represented in the following way:
From the circuit:
Ia0 = Ia1 = Ia2 =
Ea1
jX1 + jX2 + jX0 + j3Xn
Va1 = Ea1 - (jX1)(Ia1)
Va2 = 0 - (jX2)(Ia2)
Va0 = 0 - j(X0 + 3Xn)(Ia0)
With this term
we include the
value of the
grounding
reactor

14. Example: Line-to-ground fault in an unloaded generator
Assume:
X1 = X2 = 0.12 p. u. X0 = 0.06 p. u., Xn = 0 Ea1 = 1 p. u.
Ia0 = Ia1 = Ia2 =
1
p. u.
Ia = If = 3Ia1 = -j10 p. u.
Ib = 0
Ic = 0
Va0 = -jX0(Ia0) = -j0.06(-j3.33) = -0.2
Va1 = Ea1 - jX1(Ia1) = 1 - j0.12(-j3.33) = 1 - j0.4 = 0.6
Va2 = -jX2(Ia2) = -j0.12(-j3.33) = -0.4
Va
Vb
Vc
Va0
Va1
Va2
∠ °
+ +
= −










=















0
0 12 0 12 0 06
3 33
1 1 1
1
1
2
2
j
j
a a
a a
( . . . )
.





=
∠ ° ∠ °
= ∠ − °
= ∠ ° ∠ °
= ∠ + °
Va = Va0 + Va1 + Va2 = -0.2 + 0.6 - 0.4 = 0
Vb Va0 + Va1 + Va2
Vb = -0.2 + 0.6 - 0.4 = -0.2 + 0.6 - 120 -0.4 120
Vb
Vc Va0 + Va1 + Va2 = -0.2 + 0.6 120 -0.4 -120
Vc
a a
a a
a a
2
2
2
0 9165 109 1
0 9165 109 1
. .
. .

15. Line-to-line fault
a
b
c
G
Unloaded generator
If
Ia = 0 Va = ?
Ib = If Vb=Vc
Ic = -If
Ia
Ia
Ia
a a
a a
Ia
Ib
Ic
a a
a a
If
If
Ia
Ia
Ia
If
a a
a a
Ia
Ia j
If
Ia j
0
1
2
1
3
1 1 1
1
1
1
3
1 1 1
1
1
0
0
1
2
3
1 1
0 0
1
3
2
2
2
2
2
2
2










=




















=









 −




















=
−
−
−










=
=






= −
If
3






-If
0
jXn

16. +
Va1
-
+
Va2
-
+
Va0
-
Line-to-line fault
jX1
+
Ea1
-
jX2
jX0
j3Xn
Ia1
Ia2=-Ia1
Ia0=0
We have Ia1=-Ia2, Ia0=0.
This situation can be represented in the following way:
From the circuit:
Ia1 = -Ia2 =
Ea1
jX1 + jX2
Va1 = Ea1 - (jX1)(Ia1)
Va2 = Va1
Va0 = 0

17. Example: Line-to-line fault in an unloaded generator
A ssum e:
X 1 = X 2 = 0 .12 p. u . X 0 = 0 .06 p. u . , X n = 0 E a 1 = 1 p . u .
Ia1 = -Ia2 =
1
p . u .
Ia0 = 0
Phase currents during the fault are:
Ia = 0
Ib = If = -j 3 Ia1 = -7.22 p. u .
Ic = -If = 7 .22 p. u .
V a 0 = -jX 0 (Ia0) = 0
V a 1 = E a 1 - jX1(Ia1) = 1 - j0.12(-j4.1 7 ) = 1 - 0 .5 = 0 .5
V a 2 = -jX 2 (Ia2) = -j0 .12(j4.1 7 ) = 0 .5
Phase voltages during the fault are:
V a = V a 0 + V a 1 + V a 2
V a = 0 + 0 .5 + 0 .5 = 1 .0 p. u . D id not change!!!
V b V a 0 + V a 1 + V a 2
∠ °
+
= −
=
0
0 1 2 0 1 2
4 1 7
2
j
j
a a
( . . )
.
V b = 0 + 0 .5 + 0 .5 = .5(
V b p . u .
V c V a 0 + V a 1 + V a 2
V c = 0 .5(
V c p . u .
a a a a
a a
a a
2 2
2
2
0 0 5 1
0 5
0 5
0 5
+ = −
= −
=
+ = −
= −
) . ( )
.
) .
.

18. à Objective: Isolation of the problem with the
minimum service disruption
à Based on the protective device Time-Current
characteristics
à Information needed for a protection study:
o Protective device manufacturer and type
o Protective device ratings
o Trip settings and ratings
o Short circuit current at each bus
o Full load current of all loads
o Voltage level at each bus
o Power transformers data
o Instrumentation transformers ratios
Protection in Industrial Electric Networks
time
current

19. Coordination of the Protection