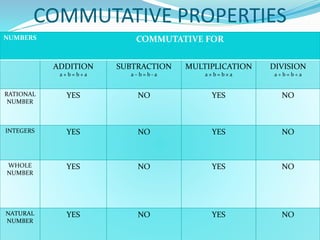
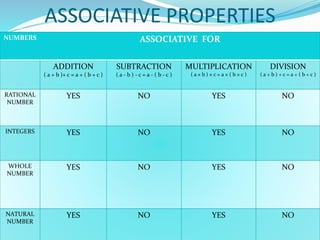
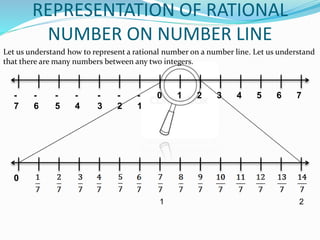
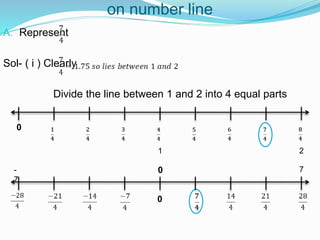
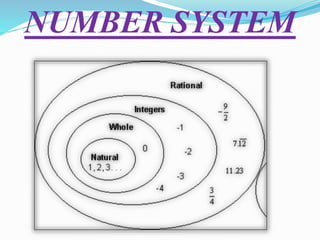
The document provides a comprehensive overview of rational numbers, including their definition, properties, and operations such as addition, subtraction, multiplication, and division. It details the closure, commutative, associative, and distributive properties specific to rational numbers, along with illustrative examples. The document also discusses additive and multiplicative identities and inverses, emphasizing the significance of these concepts in mathematics.

2. CONTENT
I. PRIOR KNOWLEDGE
II. RATIONAL NUMBER – DEFINITION
III. PROPERITIES OF NUMBERS
IV. PROPERTIES OF RATIONAL NUMBERS
V. REPRESENTATION OF RATIONAL NUMBERS ON NUMBER LINE
VI. RATIONAL NUMBERS BETWEEN TWO RATIONAL NUMBERS
VII. VARIOUS TYPES OF QUESTIONS

3. PRIOR -KNOWLEDGE
Brief knowledge on fraction, i.e fraction addition
subtraction, multiplication, and division.
Also there should be sufficient knowledge on LCM and HCF.
Some knowledge on properties of numbers that you learn in
previous classes.
Also some knowledge on number lines

4. RATIONAL NUMBERS
DEFINATION - The number which can be written in the
form of where p and q are integers and q≠0.
All the integers are rational numbers
Rational numbers are represented by ‘Q’.
Examples of Rational numbers –
, , 5 , -6 , ,
If q is equal to 0 then, becomes ‘not defined’ then
q can’t be equal to 0
Positive rational number= ,

5. NUMBER SYSTEM

6. PROPERITIES OF NUMBERS
Under the properties of numbers, we studies the following
properties of number system-
i. CLOSRE PROPERTY
 Closer under addition
 Closer under subtraction
 Closer under multiplication
 Closer under division
ii. COMMUTATIVE PROPERTY
 Commutative for addition
 Commutative for subtraction
 Commutative for multiplication
 Commutative for division

7. iii. ASSOCIATIVE PROPERTY
 Associative for addition
 Associative for subtraction
 Associative for multiplication
 Associative for division
iv. DISTRIBUTIVE PROPERTY OF MULTIPLICATION
OVER ADDITION
v. ADDITIVE INVERSE
vi. ADDITIVE IDENTITY
vii. MULTIPLICATIVE INVERSE
viii. MULTIPLICATIVE IDENTITY

8. CLOSER PROPERTY
I. CLOSER UNDER ADDITION
A number system is said to closed under addition if and only
if the result of the sum of two numbers in a system also
exist in that system. Lets understand with some number
systems that we have studied in previous classes-
a. NATURAL NUMBERS- The sum of two natural number is
always a natural number. For example- 5+7=12 (12 is a
natural number).
b. WHOLE NUMBERS- The sum of two whole number is
always a whole number. For example- 8+3=11 (11 is a
whole number) 0+0=0 (0 is whole number)

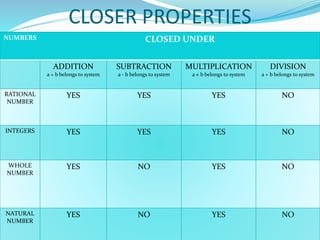
9. II. CLOSER UNDER SUBTRACTION
A number system is said to closed under subtraction if and
only if the result of the difference of two numbers in that
system also exist in that system. Lets understand with
some number systems that we have studied in previous
classes-
a. NATURAL NUMBERS- The difference of two natural
number is not always a natural number. For example- 5-
7=(-2) [-2 is not a natural number].
b. WHOLE NUMBERS- The difference of two whole number
is not always a whole number. For example- 0-5=(-5) [-5
is not a whole number]
c. INTEGERS- The difference of two integers is always a
integers . For example- (-8)-4=(-12) [-12 is a

10. III. CLOSER UNDER MULTIPLICATION
A number system is said to closed under multiplication if and
only if the result of the product of two numbers in that
system also exist in that system. Lets understand with
some number systems that we have studied in previous
classes-
a. NATURAL NUMBERS- The product of two natural
number is always a natural number. For example-
9×6=54 (54 is a natural number).
b. WHOLE NUMBERS- The product of two whole number is
always a whole number. For example- 0×5=0 (0 is a
whole number).
c. INTEGERS- The product of two integers is always a
integers . For example- (-8)×4=(-32) [-32 is a

11. IV. CLOSER UNDER DIVISION-
A number system is said to closed under division if and only
if the result of the division of two numbers in that system
also exist in that system. Lets understand with some
number systems that we have studied in previous classes-
a. NATURAL NUMBERS- The division of two natural
number is not always a natural number. For example-
5÷7= [ is not a natural number].
b. WHOLE NUMBERS- The division of two whole number is
not always a whole number. For example-
4÷0 = (not defined) [it is not a whole number]
c. INTEGERS- The division of two integers is not always a
integers . For example- (-5) ÷4 = ( ) [

12. COMMUTATIVE PROPERTY
I. COMMUTATIVE FOR ADDITION -
A number system is said to commutative under addition if and
only if the result of the sum of two numbers in a system
doesn’t depends on the order of addition. Lets understand
with some number systems that we have studied in previous
classes-
a. NATURAL NUMBERS- The sum of two natural number will
always remains same if also we change there position.For
example- 5 + 7 = 7 + 5 = 12
b. WHOLE NUMBERS- The sum of two whole number will
always remains same if also we change there position. For
example- 15 + 0 = 0 + 15 = 15

13. II. COMMUTATIVE FOR SUBTRACTION-
A number system is said to commutative under subtraction if
and only if the result of the difference of two numbers in a
system doesn’t depends on the order of subtraction. Lets
understand with some number systems that we have
studied in previous classes-
a. NATURAL NUMBERS- The difference of two natural
number will not be same if we change there position. For
example- 5 - 7 ≠ 7 - 5
⇒ (-2) ≠ (2)
b. WHOLE NUMBERS- The difference of two whole number
will not be same if we change there position. For
example- 15 - 0 ≠ 0 - 15
⇒ (15) ≠ (-15)
c. INTEGERS- The difference of two integers will not be

14. III. COMMUTATIVE FOR MULTIPLICATION-
A number system is said to commutative under multiplication
if and only if the result of the product of two numbers in a
system doesn’t depends on the order of multiplication. Lets
understand with some number systems that we have
studied in previous classes-
a. NATURAL NUMBERS- The product of two natural
number will always remains same if also we change there
position. For example- 5 × 7 = 7 × 5 = 35
b. WHOLE NUMBERS- The product of two whole number
will always remains same if also we change there
position. For example- 15 × 0 = 0 × 15 = 0
c. INTEGERS- The product of two integer will always
remains same if also we change there position. For

15. IV. COMMUTATIVE FOR DIVISION-
A number system is said to commutative under subtraction if and
only if the result of the difference of two numbers in a system
doesn’t depends on the order of subtraction. Lets understand
with some number systems that we have studied in previous
classes-
a. NATURAL NUMBERS- The division of two natural number will
not be same if we change there position. For example- 5 ÷
7 ≠ 7 ÷ 5
⇒ ≠
b. WHOLE NUMBERS- The division of two whole number will
not be same if we change there position. For example-
15 ÷ 0 ≠ 0 ÷ 15
⇒ (not defined) ≠ 0
c. INTEGERS- The division of two integers will not be same if we
change there position. For example-

16. ASSOCIATIVE PROPERTY
I. ASSOCIATIVE FOR ADDITION -
A number system is said to associative under addition if you can
add regardless of how the numbers are grouped. By 'grouped'
we mean 'how you use parenthesis'. In other words, if you are
adding it does not matter where you put the parenthesis. Lets
understand with some number systems that we have studied in
previous classes-
a. NATURAL NUMBERS- The sum of natural number will
remains same regardless of how the numbers are grouped.
For example- (5 + 7) + 3 = 5 + (7 + 3)
⇒
12 + 3 = 5 + 10 ⇒ 15 = 15
b. WHOLE NUMBERS- The sum of whole number will remains
same regardless of how the numbers are grouped. For
example- (3 + 0) + 6 = 3 + (0 + 6)

17. II. ASSOCIATIVE FOR SUBTRACTION-
A number system is said to associative under subtraction if you
can subtract regardless of how the numbers are grouped. By
'grouped' we mean 'how you use parenthesis'. In other words, if
you are subtracting it does not matter where you put the
parenthesis. Lets understand with some number systems that
we have studied in previous classes-
a. NATURAL NUMBERS- The difference of natural numbers will
change if the grouping changes . For example-
(5 - 7) - 3 ≠ 5 - (7 - 3)
⇒ (-2) -
3 ≠ 5 – (4) ⇒ (-5) ≠ 1
b. WHOLE NUMBERS- The difference of whole numbers will
change if the grouping changes. For example- (3 - 0) - 6
≠ 3 - (0 - 6)
⇒ 3 - 6 ≠ 3 + 6
⇒ (-3) ≠ (9)

18. III. ASSOCIATIVE FOR MULTIPLICATION -
A number system is said to associative under multiplication if you
can multiply regardless of how the numbers are grouped. By
'grouped' we mean 'how you use parenthesis'. In other words, if
you are multiplying it does not matter where you put the
parenthesis. Lets understand with some number systems that
we have studied in previous classes-
a. NATURAL NUMBERS- The product of natural number will
remains same regardless of how the numbers are grouped.
For example- (5 × 7) × 3 = 5 × (7 × 3)
⇒ 35 × 3 = 5 × 21 ⇒ 105 = 105
b. WHOLE NUMBERS- The sum of whole number will remains
same regardless of how the numbers are grouped. For
example- (3 × 0) × 6 = 3 × (0 × 6)
⇒ 0 ×
6 = 3 × 0 ⇒ 0 = 0

19. IV. ASSOCIATIVE FOR DIVISION-
A number system is said to associative under division if you
can divide regardless of how the numbers are grouped. By
'grouped' we mean 'how you use parenthesis'. In other
words, if you are dividing it does not matter where you put
the parenthesis. Lets understand with some number
systems that we have studied in previous classes-
a. NATURAL NUMBERS- The division of natural numbers
will change if the grouping changes . For example-
(150 ÷ 10) ÷ 5 ≠ 150 ÷ (10 ÷ 5)
⇒
(15) ÷ 5≠ 150 ÷ (2) ⇒ 3 ≠ 75
b. WHOLE NUMBERS- The division of whole numbers will
change if the grouping changes. For example- (45 ÷
9) ÷ 3 ≠ 45 ÷ (9 ÷ 3)
⇒ 5 ÷ 3 ≠
45 ÷ 3 ⇒ ≠ 15
c. INTEGERS- The division of integers will change if the
grouping changes . For example-

20. DISTRIBUTIVE PROPERTY
The distributive property of multiplication states that when
multiplying a number by the sum/difference of two numbers,
the final value is equal to the sum/difference of each addend
multiplied by the third number. Lets understand with some
number systems that we have studied in previous classes-
A. DISTRIBUTIVE PROPERTY OF MULTIPLICATION OVER
ADDITION
5 × (6 + 8)
5 × (6 + 8)
⇒ (5 × 6) + (5 × 8) OR
⇒ 5 × 14 = 70
⇒ 30 + 40 = 70
B. DISTRIBUTIVE PROPERTY OF MULTIPLICATION OVER
ADDITION
8 × (7 – 2)
8 × (7 – 2)

21. ADDITIVE INVERSE
In mathematics, the additive inverse of a number a is the
number that, when added to a, yields zero. This number is
also known as the opposite (number), sign change, and
negation. For a real number, it reverses its sign: the
opposite to a positive number is negative, and the opposite
to a negative number is positive.
For example- Additive inverse of 7 is (-7) as 7 + (-7)
= 0
ADDITIVE IDENTITY
In mathematics , the additive identity of a number is a
number that should added to the number so that we get the
number itself. When we add zero to any number we get the

22. MULTIPLICATIVE INVERSE
In mathematics, the multiplicative inverse of a number a is
the number that, when multiplied to the number, yields
one. This number is also known as the reciprocal (number)
as when we multiply a number with its reciprocal we get 1.
For example- Multiplicative inverse of 7 is as
7 × = 1
MULTIPLICATIVE IDENTITY
In mathematics, the multiplicative identity of a number a is
the number that, when multiplied to the number, gives the
number itself as a result. When we multiply one to a
number we get the number itself.
For example – Multiplicative identity of 7 is 1 as

23. PROPERITIES OF RATIONAL NUMBERS
Under the properties of numbers, we studies the following
properties of number system-
i. CLOSRE PROPERTY
 Closer under addition
 Closer under subtraction
 Closer under multiplication
 Closer under division
ii. COMMUTATIVE PROPERTY
 Commutative under addition
 Commutative under subtraction
 Commutative under multiplication
 Commutative under division

24. iii. ASSOCIATIVE PROPERTY
 Associative under addition
 Associative under subtraction
 Associative under multiplication
 Associative under division
iv. DISTRIBUTIVE PROPERTY OF MULTIPLICATION
OVER ADDITION
v. ADDITIVE INVERSE
vi. ADDITIVE IDENTITY
vii. MULTIPLICATIVE INVERSE
viii. MULTIPLICATIVE IDENTITY

25. Closer Property Of Rational Number
I. CLOSER UNDER ADDITION-
Sum of any two rational number is always a rational number.
Example - + = =
(it is a rational number)
II. CLOSER UNDER SUBTRACTION-
Difference of any two rational number is always a rational number.
Example - - = =
(it is a rational number)
III. CLOSER UNDER MULTIPLICATION-
Product of any two rational number is always a rational number.
Example - × =
(it is a rational number)
IV. CLOSER UNDER DIVISION-

26. Commutative Property Of Rational Number
I. COMMUTATIVE FOR ADDITION-
The sum of two rational number will always remains same if also we
change there position.
Example - + = + = =
II. COMMUTATIVE FOR SUBTRACTION-
The difference of two natural number will not be same if we change
there position.
Example - - ≠ - ⇒ ≠
⇒ ≠
III. COMMUTATIVE FOR MULTIPLICATION-
The sum of two rational number will always remains same if also we
change there position.
Example - × = × =

27. Associative Property Of Rational Number
I. ASSOCIATIVE FOR ADDITION-
The sum of rational number will remains same regardless of how
the numbers are grouped
Example- + [ + ] = + = OR [
+ ] + = + =
II. ASSOCIATIVE FOR SUBTRACTION-
The difference of rational numbers will change if the grouping
changes.
Example - - [ - ] ≠ [ - ] -
III. ASSOCIATIVE FOR MULTIPLICATION-
The product of rational number will remains same regardless of how
the numbers are grouped
Example - × [ × ] = × = OR [

28. Distributive Property Of Rational Number
A. DISTRIBUTIVE PROPERTY OF MULTIPLICATION
OVER ADDITION-
Lets us consider three rational numbers , ,
× [ + ]
× [ + ]
⇒ [ × ] + [ × ] OR
⇒ +
⇒ + =
⇒ + = =
B. DISTRIBUTIVE PROPERTY OF MULTIPLICATION
OVER SUBTRACTION-

29. ADDITIVE INVERSE
In mathematics, the additive inverse of a number a is the
number that, when added to a, yields zero. This number is
also known as the opposite (number), sign change, and
negation.
For example- Additive inverse of is as
+ = 0
ADDITIVE IDENTITY
In mathematics , the additive identity of a number is a
number that should added to the number so that we get the
number itself. When we add zero to any number we get the
number itself.
For example- Additive identity of is 0 as +

30. MULTIPLICATIVE INVERSE
In mathematics, the multiplicative inverse of a number a is
the number that, when multiplied to the number, yields
one. This number is also known as the reciprocal (number)
as when we multiply a number with its reciprocal we get 1.
For example- Multiplicative inverse of is as
× = 1
MULTIPLICATIVE IDENTITY
In mathematics, the multiplicative identity of a number a is
the number that, when multiplied to the number, gives the
number itself as a result. When we multiply one to a
number we get the number itself.
For example – Multiplicative identity of is 1 as

31. SUMMARISATION OF
PROPERTIES

32. CLOSER PROPERTIES
NUMBERS CLOSED UNDER
ADDITION
a + b belongs to system
SUBTRACTION
a - b belongs to system
MULTIPLICATION
a × b belongs to system
DIVISION
a ÷ b belongs to system
RATIONAL
NUMBER
YES YES YES NO
INTEGERS YES YES YES NO
WHOLE
NUMBER
YES NO YES NO
NATURAL
NUMBER
YES NO YES NO

33. COMMUTATIVE PROPERTIES
NUMBERS COMMUTATIVE FOR
ADDITION
a + b = b + a
SUBTRACTION
a – b = b - a
MULTIPLICATION
a × b = b × a
DIVISION
a ÷ b = b ÷ a
RATIONAL
NUMBER
YES NO YES NO
INTEGERS YES NO YES NO
WHOLE
NUMBER
YES NO YES NO
NATURAL
NUMBER
YES NO YES NO

34. ASSOCIATIVE PROPERTIES
NUMBERS ASSOCIATIVE FOR
ADDITION
( a + b )+ c = a + ( b + c )
SUBTRACTION
( a - b ) - c = a - ( b - c )
MULTIPLICATION
( a × b ) × c = a × ( b × c )
DIVISION
( a ÷ b ) ÷ c = a ÷ ( b ÷ c )
RATIONAL
NUMBER
YES NO YES NO
INTEGERS YES NO YES NO
WHOLE
NUMBER
YES NO YES NO
NATURAL
NUMBER
YES NO YES NO

35. DISTRIBUTIVE PROPERTY
A. DISTRIBUTIVE PROPERTY OF MULTIPLICATION OVER
ADDITION-
a × ( b + c ) = (a × b ) + (a × c)
B. DISTRIBUTIVE PROPERTY OF MULTIPLICATION OVER
SUBTRACTION-
a × ( b - c ) = (a × b ) - (a
× c)
ADDITIVE IDENTITY PROPERTY-
a + 0 = a
ADDITIVE INVERSE PROPERTY-
a + (-a) = 1

36. REPRESENTATION OF RATIONAL
NUMBER ON NUMBER LINE
-
7
-
6
-
5
-
4
-
3
-
2
-
1
0 1 2 3 4 5 6 7
Let us understand how to represent a rational number on a number line. Let us understand
that there are many numbers between any two integers.
0
1 2

37. RATIONAL NUMBERS BETWEEN
TWO RATIONAL NUMBER
 There are many rational numbers between any two rational
number
 Let the two rational numbers be
 You may thought there are only
 But if I multiply 10 in both numerator and denominator we get -
 So numbers between are
 We will find the rational numbers in two different ways
A. LCM method
B. Average method

38. LCM METHORD OF FINDING
RATIONAL NUMBER
When you are given with two rational numbers and asked to
find some rational numbers between them then follow the
steps-
STEP 1 - Make sure that the denominator of the two
fractions are same otherwise make the denominator same
by taking the LCM.
STEP 2 – If the desire number of rational numbers are
present in between the resultant rational numbers the
answer is over
STEP 3 – If desire number of rational numbers are not
obtained then multiply suitable numbers at numerator as
well as denominator and get the resultant rational numbers

39. AVERAGE METHORD OF
FINDING RATIONAL NUMBER
Let us assume that ‘x’ and ‘y’ are two rational numbers
 1st rational number between x and y is
 2nd rational number between
 3rd rational number between y and is
x
y
x
y

40. SOME IMPORTANT CONCEPTS
 Comparison of two rational numbers can be done by
making there denominator same (taking LCM) and then
comparing.
 Equality of two rational number can be checked by cross
multiplication method-
(numerator of 1st ) × (denominator of 2nd ) = (numerator of 2nd
) × (denominator of 1st )
Methods of finding prime numbers- (Sieve of
Eratosthenes) Let us assume that we are given with a
number ‘n’ and we have to check weather it is a prime
number or not.
First of all find and see all the prime numbers less
than and check weather ‘n’ is divisible by these prime
numbers or not.

41. VARIOUS TYPES OF QUESTIONS
 TYPE 1 – Application of Mathematical operations of rational
numbers (BODMAS Formula)
 TYPE 2 – Proper use of all the properties of rational numbers
 TYPE 3 – Rational numbers between two rational numbers
 TYPE 4 – Representation of rational number on number line
 TYPE 5 – Comparison of two rational numbers
 TYPE 6 – Verification of properties of rational numbers

42. operations of rational numbers (BODMAS
Formula)
A. Add
Sol-
B. Subtract
Sol-
C. Multiply
Sol-

43. rational numbers
A. Solve
Sol-

44. rational numbers
A. Find 10 rational numbers between
Sol- LCM of 6 and 8 is 24 ,so
Thus we have
and we can choose any 10 out of these.

45. on number line
A. Represent
Sol- ( i ) Clearly
Divide the line between 1 and 2 into 4 equal parts
0
1 2
0
-
7
70

46. numbers
A. Compare the rational numbers
Lets make there LCM same and then compare them. So,
and

47. numbers
A. Verify : for
, ,
We have ,
LHS =
RHS =

48. THANK YOU
ABHISHEK MISHRA
FACEBOOK PAGE- LEARNING WITH ABHISHEK
YOUTUBE - ABHISHEK MISHRA