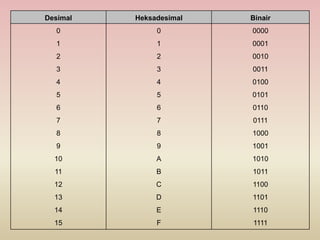
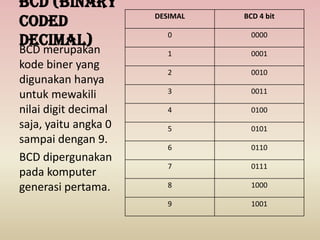
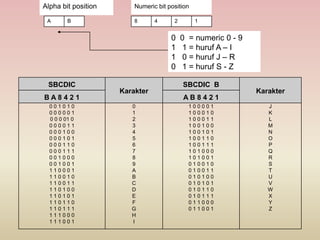
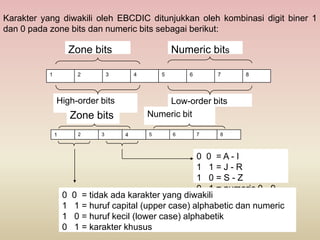
Dokumen ini membahas berbagai sistem bilangan, termasuk desimal, biner, heksadesimal, dan oktadesimal, serta cara konversi antar sistem tersebut. Juga dijelaskan tentang kode yang mewakili data dalam komputer, seperti BCD, SBCDIC, EBCDIC, dan ASCII, serta penggunaannya dalam generasi komputer yang berbeda. Penjumlahan dan pengurangan dalam berbagai sistem bilangan juga dicontohkan.

1. SISTEM BILANGAN &
KODE
TRI NURPRATIWI
41812120164

2. SISTEM BILANGAN DASAR SEPULUH
(DESIMAL)
Bilangan ialah suatu jumlah dan suku-suku angka.
Dimana tiap suku angka adalah merupakan hasil
perkalian antara angka dengan hasil perpangkatan
dan bilangan dasar, dimana pangkat ini sesuai dengan
letak suku angka tersebut.
Contoh: Bilangan 127 dalam sistem bilangan dasar
sepuluh dapat diuraikan sbb.
(127) 10 = 1 x 102 + 2 x 101 + 7 x 100
Sistem bilangan yang menggunakan kombinasi angka-
angka dan not sampai dengan sembilan.
Contoh: 123, dibaca sebagai seratus dua puluh tiga

3. SISTEM BILANGAN DASAR DUA
(SISTEM BINAIR)
Mempunyai bilangan dasar (base) = 2, karena
hanya mengenal 2 notasi yaitu 0 dan 1.
Digunakan untuk perhitungan didalam
komputer, karena komponen-komponen dasar
komputer hanya dua keadaan saja yaitu hidup
dan mati.
Contoh :
(1011)2 = 1 x 23 + 0 + 22 + 1 x 21 + 1 x 20 = (11)10

4. SISTEM BILANGAN DASAR ENAM
BELAS (SISTEM HEKSADESIMAL)
Mempunyai bilangan dasar (base) = 16.
Kombinasi dari system bilangan heksadesimal
ini dibentuk dari bilangan 0 sampai 9 dan
abjad A sampai F.
Contoh :
(AF01)16 = A x 163 + F x 162 + 0 x 161 + 1 x 160

5. SISTEM BILANGAN DASAR DELAPAN
(SISTEM OKTADESIMAL)
Mempunyai bilangan dasar (base) = 8.
Kombinasi dari system bilangan oktadesimal
ini dibentuk dari bilangan 0 sampai 7.
Contoh :
(701)8 = 7 x 82 + 0 x 81 + 1 x 80 = (449)10

6. MACAM-MACAM KONVERSI
Konversi dari system desimal
ke system binair
Bilangan Bulat
(235)10 = (…………….)2
Hasilnya: (11101011)2
Bilangan Pecahan
(0,625)10 = (………..)2
Hasilnya ( 0.101)2

7. Konversi dari system binair
ke system desimal
Bilangan Bulat
Contoh :
(10111)2 = (……………) 10
1 0 1 1 1
x x x x x
24 23 22 21 20
16 + 0 + 4 + 2 +
1 = (23)10
Bilangan Pecahan
Contoh :
( 0 111) 2 = ( ……………) 10
0 1 1 1
x x x x
2-1 2-2 2-3 2-4
0 + ¼ + 1/8 + 1/16
= (0.4375)10

8. Konversi binair ke
bilangan heksadesimal
Bilangan Bulat
( 1110110111011)2 =
(………….) 16
0001 1101 1011 1011
1 D B B
 (1DBB)16
Bilangan Pecahan
(1110110111011)2 =
(………….)16
1110 1101 1101 1000
E D D 8
 (.EDD8)16

9. Desimal Heksadesimal Binair
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111

10. Konversi bilangan
heksadesimal ke bilangan
binair
Contoh :
(ABC097)16 = (………….) 2
A B C 0 9 7
1010 1011 1100 0000 1001 0111
Hasilnya  (101010111100000010010111)2

11. Konversi
bilangan
oktadesimal
ke bilangan
binair
Contoh :
(732)8 = (………)2
7 3 2
111 011 010
(111011010)2
Konversi
bilangan
desimal ke
bilangan
oktadesimal
Contoh :
( 235) 10 = ( ……………)8
Hasilnya  ( 352) 8

12. Konversi bilangan
heksadesimal ke bilangan
oktadesimalContoh:
(AF821) 16 = ( …………..) 8
Langkah 1: Konversi dari bilangan heksadesimal ke bilangan binair
A F 8 2 1
1010 1111 1000 0010 0001
Hasil : 10101111100000100001
Langkah 2: Konversi dari bilangan binair ke bilangan oktadesimal
010 101 111 100 000 100 001
2 5 7 4 0 4 1
Hasilnya : 2574041

13. Penjumlahan
Bilangan
Penjumlahan Bilangan
Desimal
a. (125)10 + (200)10 =
125
200
----- +
325  (325)10
b. (780)10 + (236)10 =
780
236
-----+
1016  (1016)10
Penjumlahan Bilangan Binair
a. (1000)2 + (111)2 =
1000
111
------ +
1111  (1111)2
b. ( 1 1 0 1 ) 2 + ( 1 0 0 1 ) 2 =………. 2
1 1 0 1
1 0 0 1
---------- +
1 0 1 1 0  hasilnya

14. Penjumlahan Bilangan
Oktadesimal
a. ( 235)8 + (122)8 =
235
122
------ +
357  (357)8
b. ( 7 4 2 ) 8 + ( 2 1 0 ) 8 =..…8
7 4 2
2 1 0
---------- +
1 1 5 2  hasilnya
Penjumlahan Bilangan
Heksadesimal
a. (345)16 + (269)16 =
345
269
----- +
5AE  (5AE)16
c. (8DBE)16 + (CF01)16 =
8DBE
CF01
-------- +
15CBF  ( 15CBF)16

15. Pengurangan Bilangan
Pengurangan Bilangan
Desimal
a. (937)10 – (824)10 =
937
824
---- -
113  (113)10
b. (785)10 – (398)10 =
785
398
---- -
384  (384)10
Pengurangan Bilangan
Binair
a. (1110)2 + (110)2 =
1110
110
------ -
1000  (1000)2
b. (11001)2 – (111)2 =
11001
111
------- -
10010  (10010)2

16. Pengurangan bilangan
Oktadesimal
a. ( 765 ) 8 – (342)8 =
765
342
----- -
423  (423)8
b. (432)8 – (276)8 =
432
276
----- -
134  (134)8
Pengurangan bilangan
Heksadesimal
a. (9AB801)16 – ( 889601)16 =
9AB801
8 89601
---------- -
122200  (122200)16
b.(D237)16 – ( 1918)16 =
D237
1918
------ -
C91F  (C91F)16

17. Kode yang mewakili
data
• Komputer 1 byte untuk 4 bit menggunakan
kode biner yang berbentuk kombinasi 4 bit yaitu
BCD (Binary Coded Decimal).
• Komputer yang menggunakan 1 byte untuk 6
bit, menggunakan kode biner dengan kombinasi
6 bit yaitu SBCDIC (Standard Binary Coded
Decimal Interchange Code).
• Komputer 1 byte untuk 8 bit menggunakan
kode biner dengan kombinasi 8 bit yaitu EBCDIC
(Extended Binary Coded Decimal Interchange
Code) atau ASCII (American Standard Code for
Information Interchange).

18. BCD (Binary
Coded
Decimal)
DESIMAL BCD 4 bit
0 0000
1 0001
2 0010
3 0011
4 0100
5 0101
6 0110
7 0111
8 1000
9 1001
BCD merupakan
kode biner yang
digunakan hanya
untuk mewakili
nilai digit decimal
saja, yaitu angka 0
sampai dengan 9.
BCD dipergunakan
pada komputer
generasi pertama.

19. SBCDIC (Standar Binary Coded
Decimal Interchange Code)
• SBCDIC banyak digunakan pada komputer generasi
kedua.
• SBCDIC menggunakan kombinasi 6-bit, sehingga lebih
banyak kombinasi yang dihasilkan yaitu sebanyak 64 (26
= 64) kombinasi kode adalah 10 kode untuk digit angka,
26 kode untuk huruf alphabetic dan sisanya karakter-
karaker khusus yang dipilih.
• Posisi bit di SBCDIC dibagi menjadi 2 zone yaitu 2 bit
pertama (diberi nama A dan B) disebut alpha bit
position dan 4 bit berikutnya (diberi nama bit 8, bit 4
dan bit 1) disebut numeric bit position.

20. A B 8 4 2
Alpha bit position
1
Numeric bit position
0 0 = numeric 0 - 9
1 1 = huruf A – I
1 0 = huruf J – R
0 1 = huruf S - Z
SBCDIC
Karakter
SBCDIC B
Karakter
B A 8 4 2 1 A B 8 4 2 1
0 0 1 0 1 0
0 0 0 0 0 1
0 0 0 01 0
0 0 0 0 1 1
0 0 0 1 0 0
0 0 0 1 0 1
0 0 0 1 1 0
0 0 0 1 1 1
0 0 1 0 0 0
0 0 1 0 0 1
1 1 0 0 0 1
1 1 0 0 1 0
1 1 0 0 1 1
1 1 0 1 0 0
1 1 0 1 0 1
1 1 0 1 1 0
1 1 0 1 1 1
1 1 1 0 0 0
1 1 1 0 0 1
0
1
2
3
4
5
6
7
8
9
A
B
C
D
E
F
G
H
I
1 0 0 0 0 1
1 0 0 0 1 0
1 0 0 0 1 1
1 0 0 1 0 0
1 0 0 1 0 1
1 0 0 1 1 0
1 0 0 1 1 1
1 0 1 0 0 0
1 0 1 0 0 1
0 1 0 0 1 0
0 1 0 0 1 1
0 1 0 1 0 0
0 1 0 1 0 1
0 1 0 1 1 0
0 1 0 1 1 1
0 1 1 0 0 0
0 1 1 0 0 1
J
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y
Z

21. EBCDIC (Extended Binary Coded Decimal
Interchange Code) atau ASCII (American
Standard Code for Information Interchange).
• EBCDIC banyak digunakan pada computer
generasi ketiga, seperti IBM S/360.
• EBCDIC terdiri dari kombinasi 8-bit yang
memungkinkan untuk mewakili karakter
sebanyak 256 (2 8 = 256) kombinasi karakter. Pada
EBCDIC high-order bits atau 4-bit pertama
disebut dengan zone bits dan low-order bits atau
4 bit kedua disebut dengan numeric bits.

22. 1 2 3 4 5 6 7 8
Zone bits Numeric bits
High-order bits Low-order bits
1 2 5 6 7
Zone bits
8
Numeric bit
0 0 = A - I
1 1 = J - R
1 0 = S - Z
0 1 = numeric 0 - 9
43
0 0 = tidak ada karakter yang diwakili
1 1 = huruf capital (upper case) alphabetic dan numeric
1 0 = huruf kecil (lower case) alphabetik
0 1 = karakter khusus
Karakter yang diwakili oleh EBCDIC ditunjukkan oleh kombinasi digit biner 1
dan 0 pada zone bits dan numeric bits sebagai berikut:

23. ASCII 7-bit
ASCII singkatan dari American Standard Code
for Information Interchange,dikembangkan
oleh ANSI (American National Standards
Institute) untuk tujuan membuat kode biner
yang standar. Kode ASCII yang standar
menggunakan kombinasi 7-bit, dengan
kombinasi sebanyak 127 dari 128 (27 =
128).ASCII 7-bit banyak digunakan untuk
komputer-komputer generasi sekarang,
termasuk komputer mikro.

24. Kemungkinan kombinasi ASCII , yaitu
26 buah huruf capital (upper case) dari A s/d Z
26 buah huruf kecil (lower case) dari a s/d z
digit decimal dari 0 s/d 9
34 karakter kontrol yang tidak dapat dicetak
hanya digunakan untuk informasi status operasi
computer
32 karakter khusus (special characters)

25. ASCII 8-bit
ASCII 8-bit terdiri dari kombinasi 8-bit
mulai banyak digunakan, karena lebih
banyak memberikan kombinasi karakter.
Dengan ASCII 8-bit, karakter-karakter
graphic yang tidak dapat diwakili ASCII 7-
bit, seperti ♥ ♦ ♣ ♠ α β ►◄ karakter dan
sebagainya dapat diwakili. Komputer IBM
PC menggunakan ASCII 8-bit.