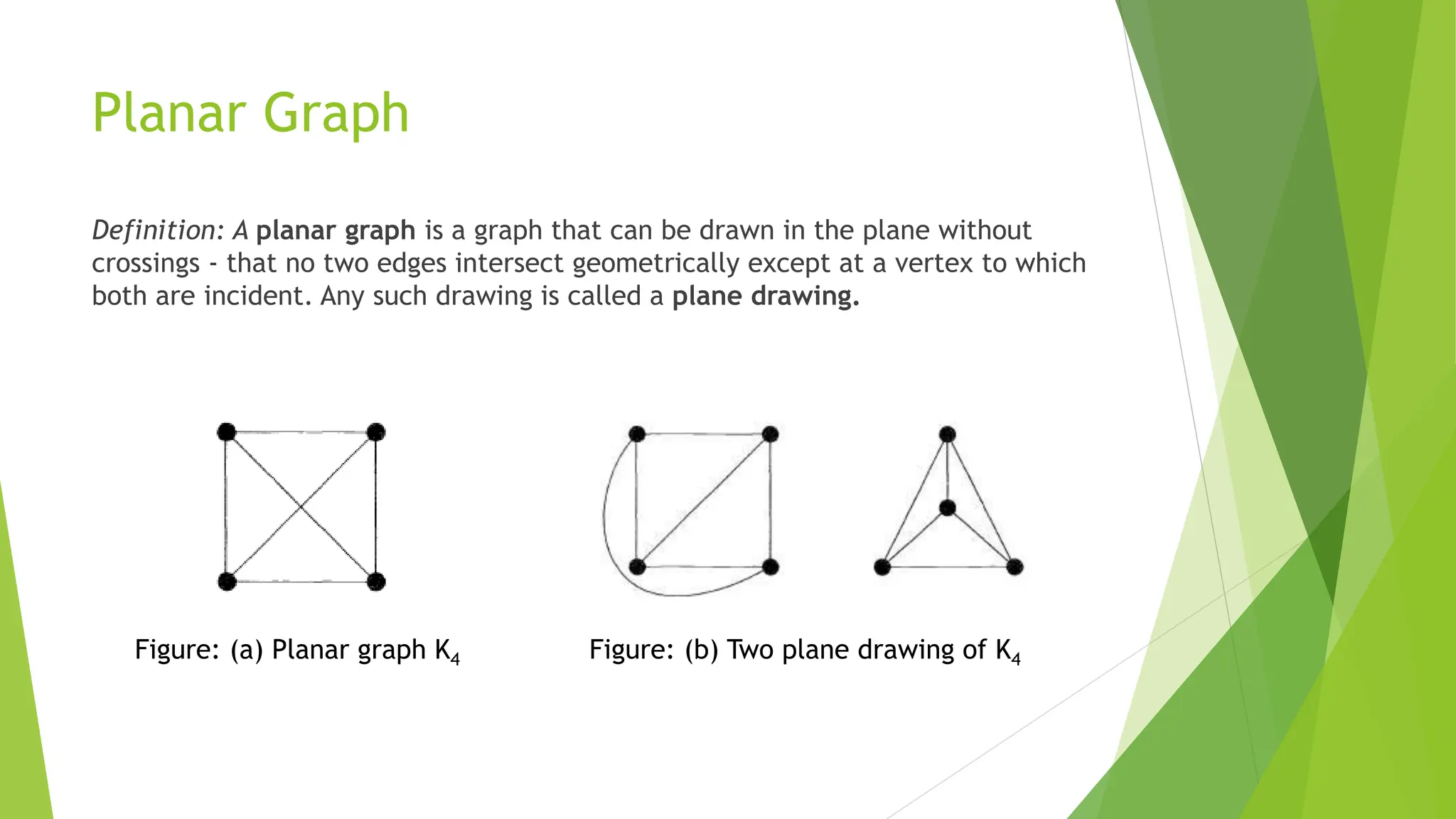
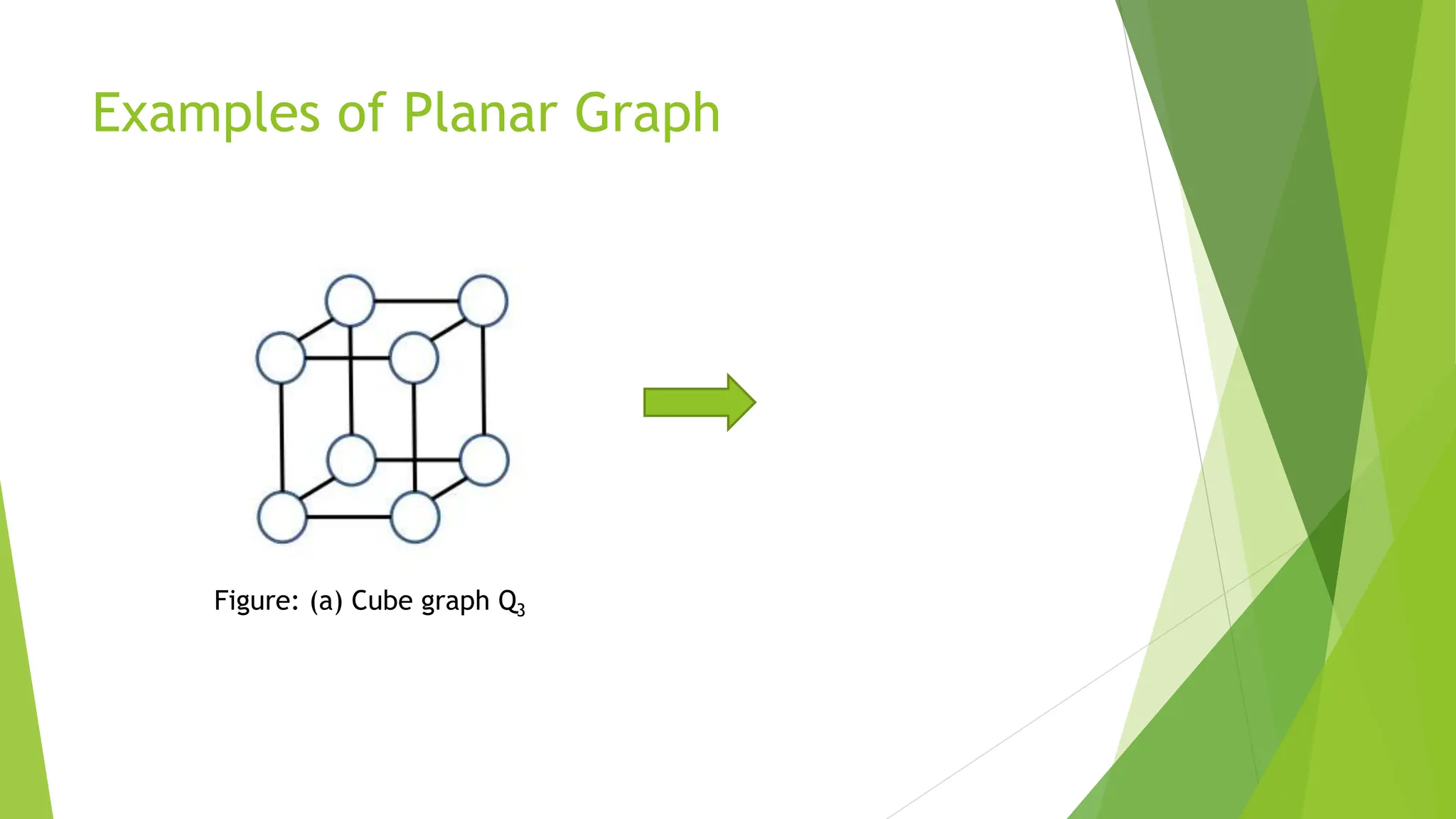
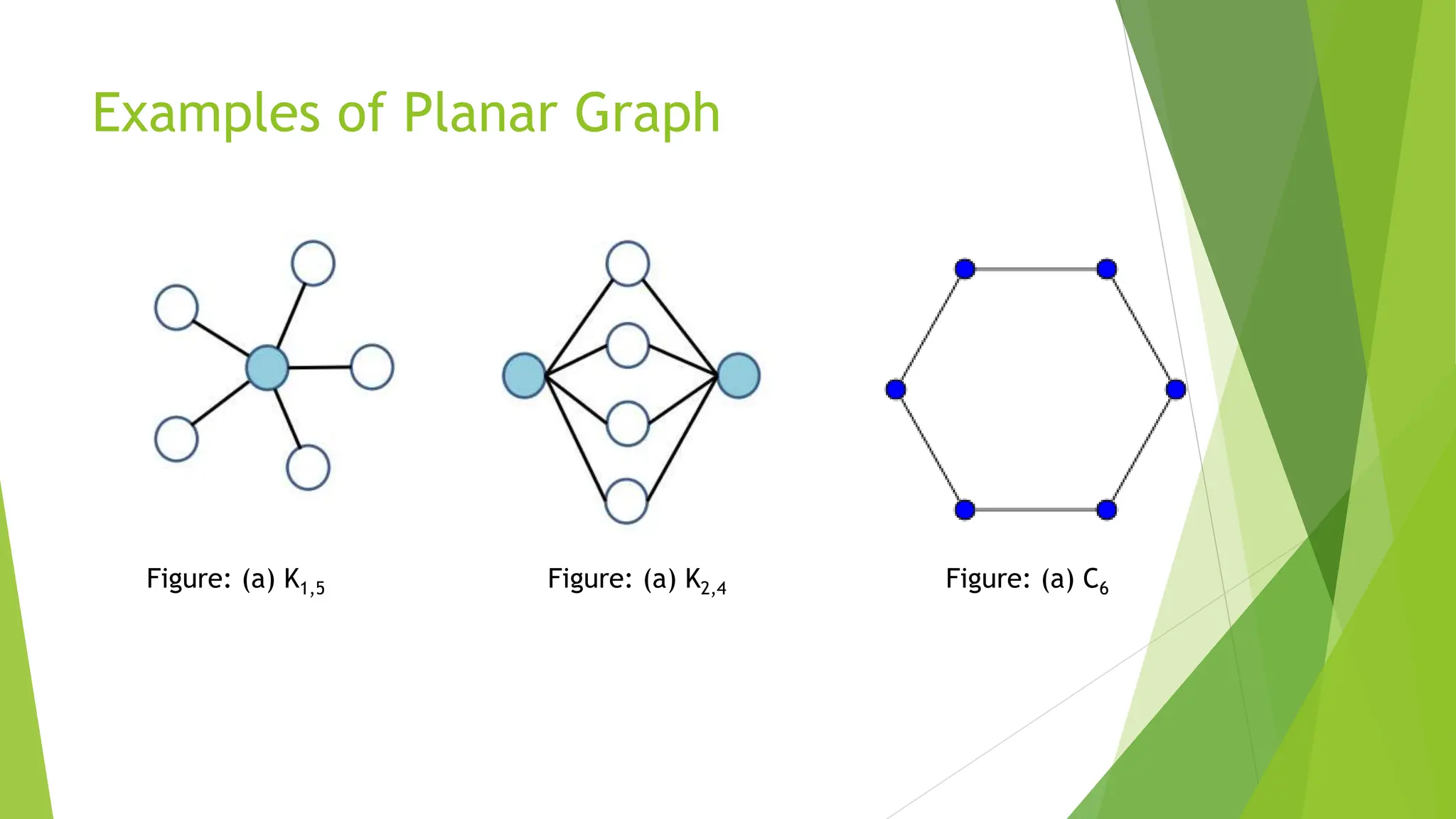
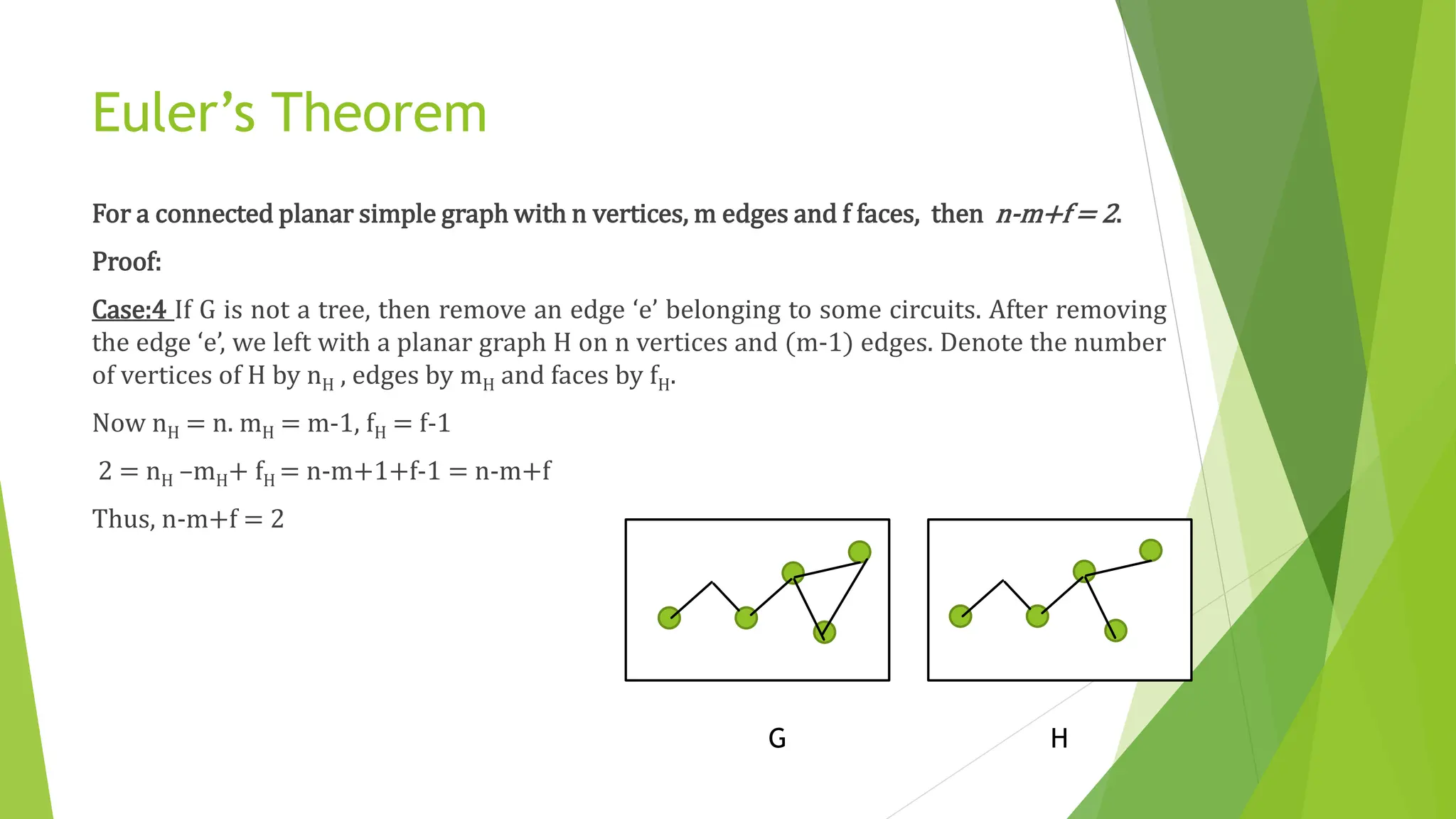
The document discusses the planar graph three utilities problem, focusing on the conditions under which a graph can be drawn without crossing edges. It defines planar graphs, describes planarity testing, and presents Kuratowski's theorem as well as Euler's theorem, which relate to the properties of planar graphs. Additionally, it outlines corollaries regarding the maximum number of edges in relation to vertices, particularly for graphs without triangles.

1. Planar Graph

2. Three Utilities Problem
 Can each house be connected to each utility, with no connection lines crossing?

3. Planar Graph
Definition: A planar graph is a graph that can be drawn in the plane without
crossings - that no two edges intersect geometrically except at a vertex to which
both are incident. Any such drawing is called a plane drawing.
Figure: (a) Planar graph K4 Figure: (b) Two plane drawing of K4

4. Examples of Planar Graph
Figure: (a) Cube graph Q3

5. Examples of Planar Graph
Figure: (a) K1,5 Figure: (a) K2,4 Figure: (a) C6

6. Examples of Non-Planar Graph
Figure: (a) K5 Figure: (b) K3,3

7. Detection of Planarity
1. Since addition/removal of self loops does not effect planarity, remove all self loops
2. Eliminate edges in parallel by removing all but one edge between every pair of
vertices
3. Elimination of a vertex of degree two by merging two edges in series
The resultant graph:
 Single edge
 K4
 Non-separable simple graph with n>=5 and e>= 7
 Then check if e <= 3n-6 satisfies
The graph is Planar
The graph is Planar

8. Kuratowski's Theorem: Planarity Testing
THEOREM: (Kuratowski, 1930). A graph is planar if and only if it contains
no subgraph homeomorphic to K5 or K3,3.
Homeomorphism: Two graphs G and G’ are homeomorphic if there is an
isomorphism from some subdivision of G to some subdivision of G’

9. Kuratowski's Theorem: Planarity Testing
Show that the Petersen graph is non-planar:

10. Euler’s Theorem
For a connected planar simple graph with n vertices, m edges and f faces, then n-m+f = 2.
Proof:
Case:1
Suppose that m =0.Then for G to be a connected plane graph there must be only one vertex and
one face. So, n=1, m=0, f=1. Now, n-m+f = 1-0+1 = 2
Case:2
For m=1, there n=1 m=1 f=2.
Now, n-m+f = 1-1+2 = 2
For m=1, there n=2 m=1 f=1
Now, n-m+f = 2-1+1= 2
Case:3 If G is tree, then
there m=n-1, f=1.
Now, n-m+f = n-(n-1)+1= 2
Tree

11. Euler’s Theorem
For a connected planar simple graph with n vertices, m edges and f faces, then n-m+f = 2.
Proof:
Case:4 If G is not a tree, then remove an edge ‘e’ belonging to some circuits. After removing
the edge ‘e’, we left with a planar graph H on n vertices and (m-1) edges. Denote the number
of vertices of H by nH , edges by mH and faces by fH.
Now nH = n. mH = m-1, fH = f-1
2 = nH –mH+ fH = n-m+1+f-1 = n-m+f
Thus, n-m+f = 2
G H

12. Corollary
If G is a connected simple finite plane graph with n vertices (n≥ 3), then G has at most (3n-6)
edges. Furthermore, if G contains no triangles, then G has at most (2n-4) edges.
Proof: Suppose that G has m edges and f faces consider the number of pairs (e, F) where, e is one of
the edges bounding the face F.
For each edge, there are at most 2 faces that it bounds. So the total number of edge-face pairs have
to be less than 2m. On the other hand, because G is a simple graph, each face is bounded by at least
3 edges. So the total number of edge face pairs is greater than or equal to 3f.
3f ≤ 2m.
Now from Euler’s Theorem
n-m+f = 2
3n – m +3f =6
3f = 6-3n+3m
2m 6-3n+3m
2m-3m ≥ 6-3n
-m ≥ 6-3n
m≤ 3n-6 [Multiplied by -1]
Try by yourself:
If G contains no triangles, then G has at most (2n-4) edges.
e1
e2
e3
e4
e5
e5
e6
e7
e8
e9
e10
F1
F2
F3
F4
F5
Infinite face Here, n=8 m=10 and f = 5
No. of edge face pairs = 19
19 ≤ 2*10
19 ≥ 3*5

13. Corollary
Every finite simple plane graph has a vertex of degree less than 6.
Proof: Suppose G is a finite, simple plane graph with n vertices, m edges and the vertex j has
degree dj (1≤j ≤ n). Now from Handshaking theorem we know,
𝑗=1
𝑛
𝑑𝑗=2m
≤ 2 (3n-6) [m ≤ 3n-6]
≤ 6n-12
If each vertex had degree 6 or more, then the degree sum would be at least 6n. Thus there is
at least one vertex whose degree has less than 6.
Try by yourself:
Every finite simple plane graph (If there is no triangle) has a vertex of degree less than 4.