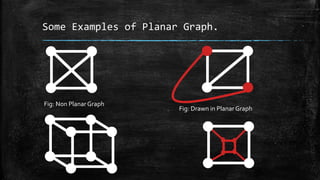
This document discusses planar graphs, including: - Definitions of planar graphs and examples. - Theorems like Kuratowski's and Euler's theorems about planar graphs. - Algorithms for planarity testing and drawing planar graphs. - Applications of planar graphs in VLSI circuits, computer vision, and electrical circuit design.

1. PLANAR GRAPH
ALGORITHMS & APPLICATIONS.

2. PREPARED BY
▪ SHAKIL AHMED

3. OUTLINE
▪ Definition of Planar Graph.
▪ Some Examples.
▪ Some Notations.
▪ SomeTheorems.
▪ Kuratowski /WagnerTheorem.
▪ EulerTheorem.
▪ Some Corollaries.
▪ Non Planarity.
▪ K3,3 and k5 is not Planar Graph.
▪ Drawing of a Planar Graph.
▪ PlanarityTesting.
▪ Algorithms.
▪ Applications.
▪ VLSICircuits.
▪ References.

4. What is Planar Graph?
▪ Plane :
Our world has three dimensions, but there are only two dimensions on a plane :
▪ Length(x) and Width(y) makes a Plane.
▪ No thickness and goes on forever.
▪ Planar Graph :
▪ It is a simple Graph.
▪ Can be drawn on the plane without edge crossings.

5. Some Examples of Planar Graph.
Fig: Drawn in Planar Graph
Fig: Non PlanarGraph

6. Some Notations.
▪ Faces
▪ Divide the Plane in many regions.
– Exterior face.
– Interior faces.
▪ Each edge is incident to 2 faces, except in special cases:
f1 f2
f3
f4
Exterior
Face

7. Some Theorems
▪ Kuratowski’s theorem (Ref-1)
– Theorem (Kuratowski, Wagner, 193*)
A graph is planar, if and only if it does not contain the K5 and the K3,3 as a
homeomorphic subgraph / as a minor.
▪ H is a minor of G, if H can be obtained from G by a series of or more
deletions of vertices, deletions of edges, and contraction of edges.
▪ Does not yield fast recognition algorithm!

8. Euler’s Theorem.
▪ Theorem (Euler)
Let G be a connected plane graph with n vertices, m edges,
and f faces.Then n + f – m = 2.
▪ Proof. By induction.
– True if m=0.
– If G has a circuit, then delete an edge
– If G has a vertex v of degree 1, then delete v

9. Euler’s Theorem Corollaries.
▪ Corollary 1: For any simple, connected, planar
– graph G, with |E| > 2, the following holds:
– |E| ≤ 3n – 6
▪ Proof:
▪ Each face is bounded by at least 3 edges, so:
Σd( fi) ≥ 3f
▪ Substitute 3f with 6 – 3n + 3|E|, and use the lemma.

10. Euler’s Theorem Corollaries. (Cont..)
▪ Corollary 2: For any simple
connected bipartite planar graph G,
with |E| > 2, the following holds:
▪ |E| ≤ 2n – 4
▪ Proof:
▪ Each face of G is bounded by at
least 4 edges.
▪ The result then follows as for the
previous corollary.
▪ Corollary 3: In a simple,
connected, planar graph there
exists at least one vertex of
degree at most 5.
▪ Proof:
▪ Without loss of generality we can
assume the graph to be connected,
and to have at least three vertices.
▪ If each vertex has degree at least
6, then we have 6n ≤ 2m, and so
3n ≤ m.
▪ It follows immediately from
previous Corollary that 3n ≤ 3n
— 6, which is a contradiction

11. Non Planarity.
▪ The House-and-Utilities Problem (Ref- 4)

12. The smallest graphs that are not planar.
▪ K5, K3,3
Ref - 1 & 4

13. The Petersen graph is not planar, as it has K3,3 as
minor.
Ref - 1 & 4

14. Drawing Of a Planar Graph.
In steps:
1. Test if G is planar, and
2. Find for each vertex, a
clockwise ordering of its
incident edges, such that
these orderings allow a
planar embedding, and
then
3. Assign coordinates to
vertices
▪ Different types
▪ Vertices are:
– Points in 2-dimensional space
– Rectangles, other objects
▪ Edges are
– Straight lines
– Curves
– Lines with bends
– Adjacencies or intersections of objects

15. Planarity Testing.
▪ Simple tests
▪ Following the simplifications, two elementary tests can be applied:
– If e < 9 or n < 5 then the graph must be planar.
– If e > 3n – 6 then the graph must be non-planar.
▪ If these tests fail to resolve the question of planarity, then we need to
use a more elaborate test.
Ref - 5

16. Planarity Testing Algorithms.
▪ Notations:
▪ Let B be any bridge of G relative to H.
▪ B can be drawn in a face f of H', if all the points of contact of B are in
the boundary of f.
▪ F(B,H): Set of faces of H' in which B is draw able.
▪ The algorithm finds a sequence of graphs G1, G2, …, such that Gi ⊂
Gi+1.
▪ If G is non-planar then the algorithm stops with the discovery of some
bridge B, for which F(B,Gi) = ∅
Ref - 5

17. Planarity Testing Algorithms. (Cont..).
Ref - 5

18. Planarity Testing Algorithms. (Cont..).
1
2
8
7
5
4
3 6
6
1
5
4
F2
2
3
6
1
5
4
F2
2
3
F1
F1
F3
6
1
5
4
F2
2
3
F1
F3
F47
6
1
5
4
F2
2
3
F1
F3
F4
7F5
6
1
5
4
F2
2
3
F1
F3
F4
7F5
F6
Ref - 5

19. Planarity Testing Algorithms. (Cont..).
Ref - 5
6
1
5
4
F2
2
3
F1
F3
F4
7F5
F6
F7
6
1
5
4
F2
2
3
F1
F3
F4
7F5
F6
F7
F8
6
1
5
4
F2
2
3
F1
F3
F4
7F5
F6
F7
F8
F9
6
1
5
4
F2
2
3
F1
F3
F4
7F5
F6
F7
F8
F9
F10

20. Planarity Testing Algorithms. (Cont..)
▪ Algorithm terminates when , f = e – n + 2:
▪ 16 – 8 + 2 = 10 = f
6
1
5
4
F2
2
3
F1
F3
F4
7F5
F6
F7
F8
F9
F10

21. Applications.
▪ Applications:
– Visually representing a network (e.g., social network, organization
structure, data bases (ER-diagrams), software (e.g., UML-diagrams),
flow charts, phylogenetic trees (biology, evolution), …
– Design of “chip” layout (VLSI)

22. Applications : (Electrical Circuits).
 Genus and crossing number have importance in the
manufacture of electrical circuits on planar sheets.
 A convenient method:
 Divide the circuit into planar sub circuits
 Separate them with insulating sheets
 Make connections between sub circuits, at the
vertices of the graph. X’ Y’
crossing
point
X Y
Ref - 3

23. Applications : (Computer Vision).
▪ In ComputerVision there is an abundance of problems that can be
addressed as finding a minimal cut through a planar graph.
▪ such as shape matching, image segmentation
▪ or cyclic time series.
Ref - 2

24. References.
1. Kuratowski, Kazimierz (1930), "Sur le problème des courbes gauches
en topologie" (PDF), Fund. Math. (in French), 15: 271–283.
2. Efficient Planar Graph Cuts with Applications in ComputerVision, IEEE
Computer Society Conference on ComputerVision and Pattern Recognition 2009,
Miami, Florida. c IEEE.
3. Design Of Integrated Circuits And Systems,Vol. 22, No. 5, May
2003, Pp 584-592.
4. Dudeney, Henry (1917), "Problem 251 –Water, Gas, and Electricity",
Amusements in mathematics,Thomas Nelson
5. K.S Booth ‘Testing graph planarity’ j-comp syst.sci (1976)