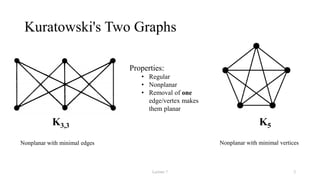
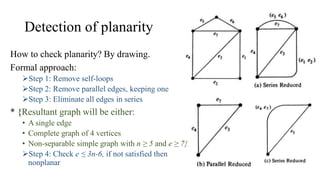
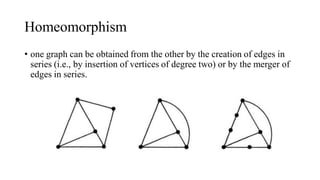
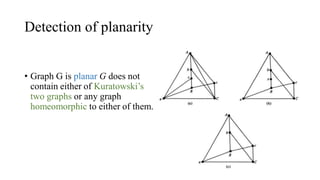
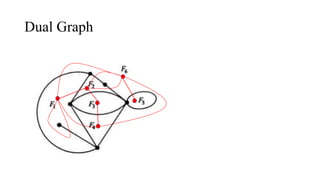
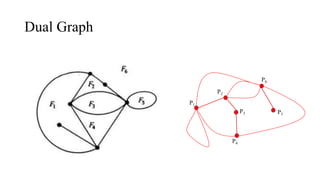
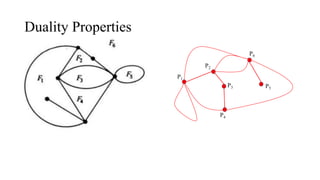
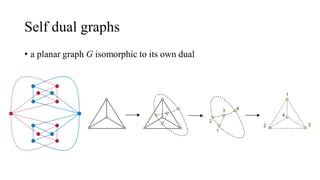
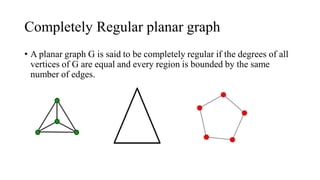
The document discusses planarity and dual graphs, focusing on Kuratowski's two graphs and properties of nonplanar graphs that become planar upon the removal of edges or vertices. It outlines a formal method for checking graph planarity and defines key concepts such as dual graphs, thickness, crossing number, and self-dual graphs. Additionally, it highlights the relationships between graph properties and conditions for planarity.

1. Planarity & Dual Graph
A.B.M. Ashikur Rahman

2. Kuratowski's Two Graphs
Lecture 7 2
Properties:
• Regular
• Nonplanar
• Removal of one
edge/vertex makes
them planar
K3,3 K5
Nonplanar with minimal edges Nonplanar with minimal vertices

3. Detection of planarity
How to check planarity? By drawing.
Formal approach:
Step 1: Remove self-loops
Step 2: Remove parallel edges, keeping one
Step 3: Eliminate all edges in series
* {Resultant graph will be either:
• A single edge
• Complete graph of 4 vertices
• Non-separable simple graph with n ≥ 5 and e ≥ 7}
Step 4: Check e ≤ 3n-6, if not satisfied then
nonplanar

4. Homeomorphism
• one graph can be obtained from the other by the creation of edges in
series (i.e., by insertion of vertices of degree two) or by the merger of
edges in series.

5. Detection of planarity
• Graph G is planar G does not
contain either of Kuratowski’s
two graphs or any graph
homeomorphic to either of them.

6. Dual Graph

7. Dual Graph
P1
P5
P4
P3
P6
P2

8. Dual Graph
Some Properties:
- Self-loop yields a pendant edge
(Vice-versa)
- Edges in series yields parallel edges
(Vice-versa)
- G* is also planar
G
{n, e, f, r, µ}
G*
{n *, e *, f *, r *, µ *}
- n* = f,
e* = e,
f* = n.
- r* = µ,
µ* = r.
P1 P5
P4
P3
P6
P2

9. Duality Properties
P1
P5
P4
P3
P6
P2

10. Thickness & Crossing
• Thickness: The least number of planar subgraphs whose union is the
given graph G.
• Thickness of a planar graph is 1
• Crossings: the fewest number of crossings (or intersections) necessary
in order to “draw” the graph in a plane?
• Crossing number of planar graph is 0
• Kuratowski’s graphs have a crossing number of 1.

11. Self dual graphs
• a planar graph G isomorphic to its own dual

12. Completely Regular planar graph
• A planar graph G is said to be completely regular if the degrees of all
vertices of G are equal and every region is bounded by the same
number of edges.