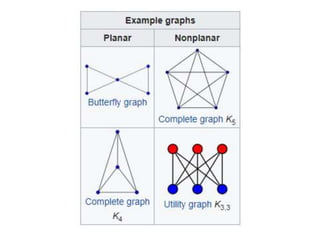
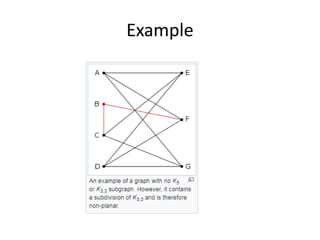
The document defines planar graphs, which can be drawn on a plane without edges crossing, and discusses their properties, including genus and planarity criteria. It covers Kuratowski's and Wagner's theorems that characterize planar graphs based on forbidden subgraphs and minors, respectively. Additionally, it presents planarity testing algorithms and inequalities related to edges, vertices, and faces in planar graphs.

1. Planar graph

2. Plan
1. Definition of the planar graph.
2. Kuratowski's and Wagner's theorems.
3. Planarity criteria.

3. 1. Definition of the planar graph.
A planar graph is a graph that can be embedded in
the plane, i.e., it can be drawn on the plane in such a way
that its edges intersect only at their endpoints. In other
words, it can be drawn in such a way that no edges cross
each other. Such a drawing is called a plane
graph or planar embedding of the graph. A plane graph
can be defined as a planar graph with a mapping from
every node to a point on a plane, and from every edge to
a plane curve on that plane, such that the extreme points
of each curve are the points mapped from its end nodes,
and all curves are disjoint except on their extreme points.

5. Plane graphs can be encoded by combinatorial
maps. A combinatorial map is
a combinatorial object
modelling topological structures with subdivided
objects.

6. A Planar graphs
Planar graphs generalize to graphs drawable on a
surface of a given genus. In this terminology, planar
graphs have graph genus 0, since the plane (and the
sphere) are surfaces of genus 0.
genus (plural genera) has a few different, but
closely related, meanings. The most common
concept, the genus of an (orientable) surface, is the
number of "holes" it has, so that a sphere has genus
0 and a torus has genus 1.

7. A sphere

8. A TORUS
In geometry, a torus (plural tori) is a surface of
revolution generated by revolving
a circle in three-dimensional space about an axis
that is coplanar with the circle.

9. Genus of orientable surfaces
In simpler terms, the value of an orientable
surface's genus is equal to the number of
"holes" it has.

10. SUMMARIZING
• The genus of a graph is the minimal integer n such that the
graph can be drawn without crossing itself on a sphere
with n handles (i.e. an oriented surface of genus n). Thus,
a planar graph has genus 0, because it can be drawn on a
sphere without self-crossing.
• The non-orientable genus of a graph is the minimal
integer n such that the graph can be drawn without
crossing itself on a sphere with n cross-caps (i.e. a non-
orientable surface of (non-orientable) genus n). (This
number is also called the demigenus.)
• The Euler genus is the minimal integer n such that the
graph can be drawn without crossing itself on a sphere
with n cross-caps or on a sphere with n/2 handles.

11. 2. Kuratowski's and Wagner's theorems
The Polish mathematician Kazimierz Kuratowski provided a
characterization of planar graphs in terms of forbidden graphs, now
known as Kuratowski's theorem:
A finite graph is planar if and only if it does not contain a subgraph that
is a subdivision of the complete graph K5 or the complete bipartite
graph K3,3 (utility graph). A subdivision of a graph results from inserting
vertices into edges (for example, changing an edge •——• to •—•—•)
zero or more times.
An example of a graph with no K5 or K3,3 subgraph. However, it
contains a subdivision of K3,3 and is therefore non-planar.
Instead of considering subdivisions, Wagner's theorem deals
with minors:
A finite graph is planar if and only if it does not have K5 or K3,3 as
a minor.

12. Example

13. A Forbidden graphs
In graph theory, a branch of mathematics, many
important families of graphs can be described by
a finite set of individual graphs that do not
belong to the family and further exclude all
graphs from the family which contain any of
these forbidden graphs as (induced) subgraph or
minor.

14. A minor of the grafp
In graph theory, an undirected graph H is called
a minor of the graph G if H can be formed
from G by deleting edges and vertices and
by contracting edges.

15. Subdivision and smoothing
In general, a subdivision of a graph G (sometimes
known as an expansion) is a graph resulting from the
subdivision of edges in G.
The subdivision of some edge e with endpoints
{u,v} yields a graph containing one new vertex w, and
with an edge set replacing e by two new edges, {u,w}
and {w,v}. For example, the edge e, with endpoints
{u,v}:

16. Subdivision

17. Smoothing out
The reverse operation, smoothing
out or smoothing a vertex w with regards to the
pair of edges (e1 ,e2 ) incident on w, removes both
edges containing w and replaces (e1 ,e2 ) with a new
edge that connects the other endpoints of the pair.
Here it is emphasized that only 2-valent
vertices can be smoothed. For example, the
simple connected graph with two edges, e1 {u,w}
and e2 {w,v}:

18. Smoothing out

19. Other planarity criteria
In practice, it is difficult to use Kuratowski's
criterion to quickly decide whether a given
graph is planar. However, there exist
fast algorithms for this problem: for a graph
with n vertices, it is possible to determine in
time O(n) (linear time) whether the graph may
be planar or not (see planarity testing).

20. Other planarity criteria
For a simple, connected, planar graph with v vertices
and e edges and f faces, the following simple conditions hold for v ≥ 3:
• Theorem 1. e ≤ 3v − 6;
• Theorem 2. If there are no cycles of length 3, then e ≤ 2v − 4.
• Theorem 3. f ≤ 2v − 4.
In this sense, planar graphs are sparse graphs, in that they
have only O(v) edges, asymptotically smaller than the maximum O(v2).
The graph K3,3, for example, has 6 vertices, 9 edges, and no cycles of
length 3. Therefore, by Theorem 2, it cannot be planar. These
theorems provide necessary conditions for planarity that are not
sufficient conditions, and therefore can only be used to prove a graph
is not planar, not that it is planar. If both theorem 1 and 2 fail, other
methods may be used.

21. A sparse graph
A dense graph is a graph in which the number of
edges is close to the maximal number of edges.
The opposite, a graph with only a few edges, is
a sparse graph. The distinction between sparse
and dense graphs is rather vague, and depends
on the context.

22. • For undirected simple graphs, the graph
density is defined as:
• For directed simple graphs, the graph density
is defined as:

23. Euler's formula
Euler's formula states that if a finite, connected,
planar graph is drawn in the plane without any
edge intersections, and v is the number of
vertices, e is the number of edges and f is the
number of faces (regions bounded by edges,
including the outer, infinitely large region), then
v-e+f=2.