Embed presentation
Downloaded 11 times





The document is a presentation by Pritam Chandra Shil on isomorphism, derived from Greek terms meaning 'equal form or shape'. It explains the concept of graph isomorphism, detailing conditions for two graphs to be isomorphic and its applications in organic chemistry. The document also touches on the complexity of the graph isomorphism problem and its classification in NP.
Introduction to the presentation and the presenter details.
Definition of isomorphism in mathematics, highlighting its properties as a bijective morphism.
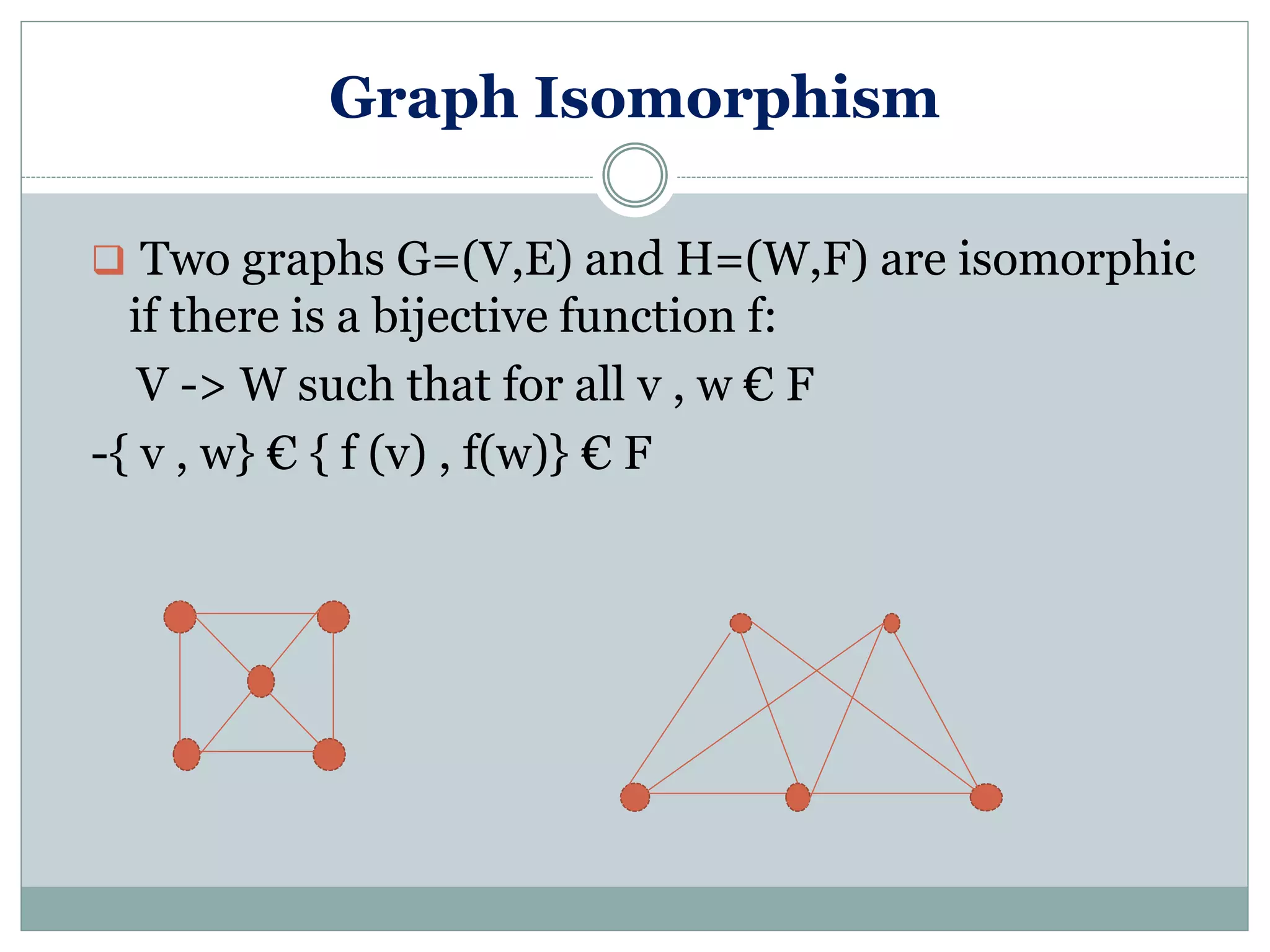
Explanation of graph isomorphism with the definition and conditions for two graphs to be isomorphic.
Conditions for labeled graphs to be isomorphic and its application in organic chemistry.
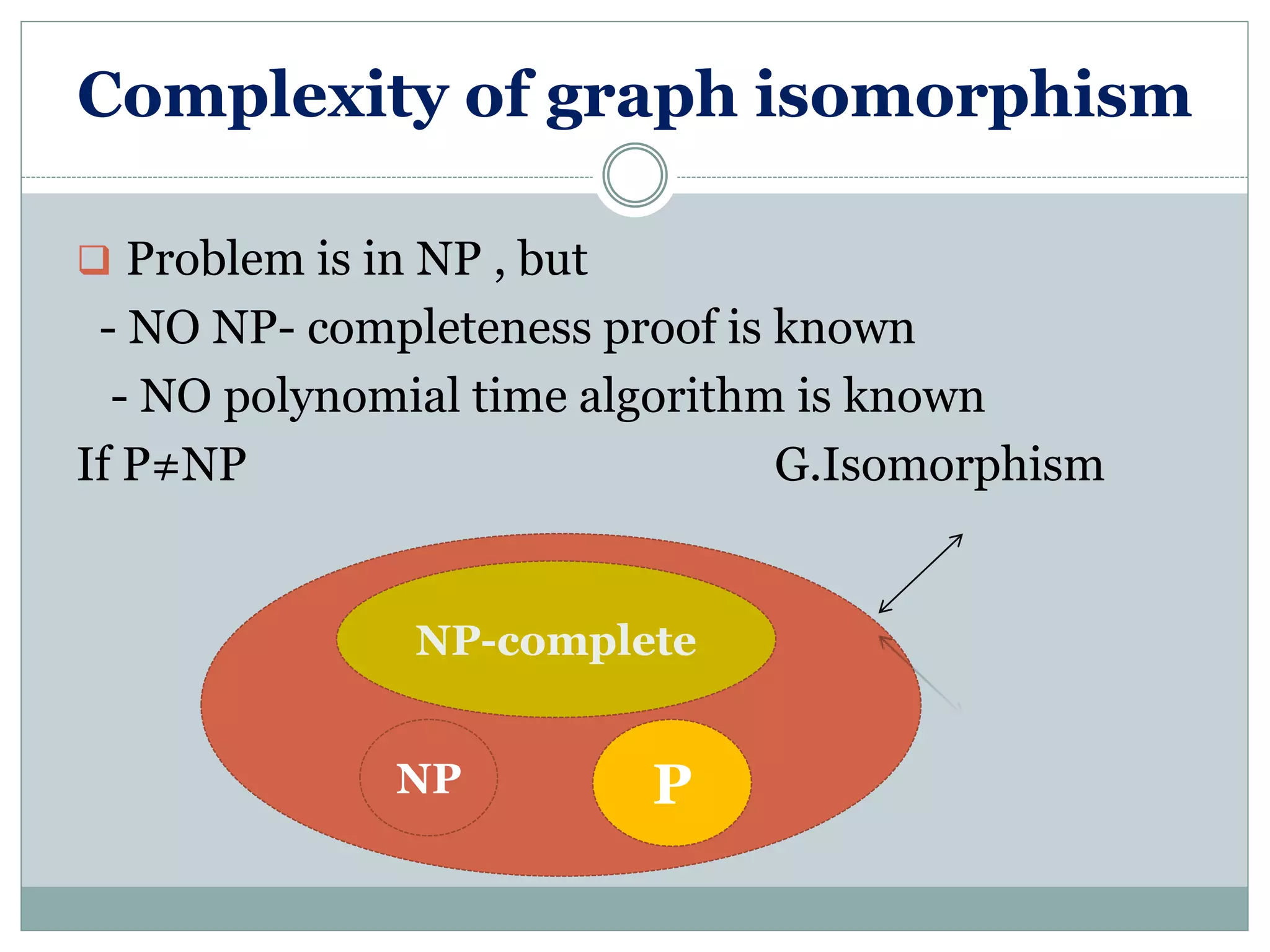
The complexity status of graph isomorphism, noting it is in NP without proofs for NP-completeness.
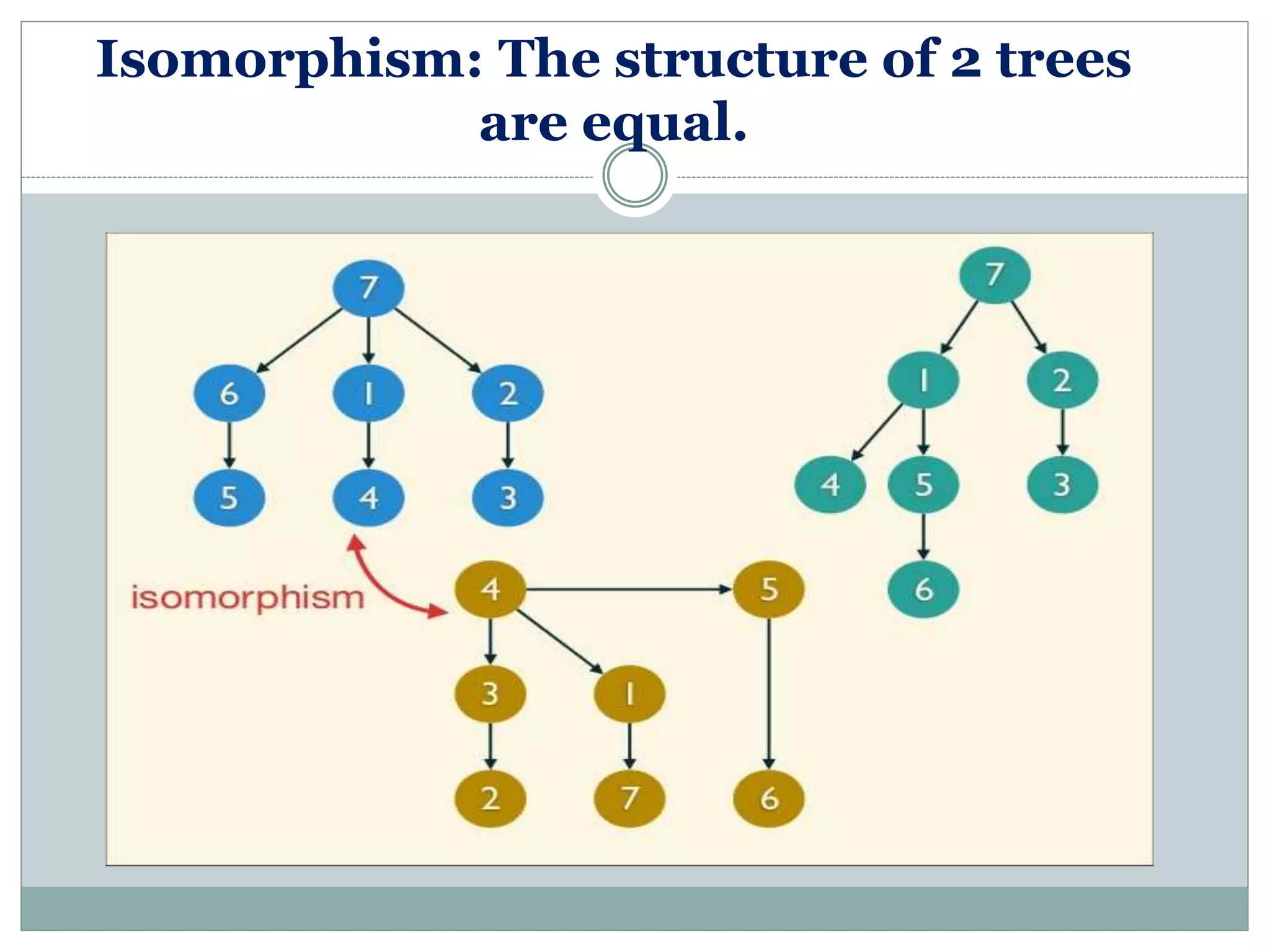
Illustrates that isomorphic trees share the same structure.
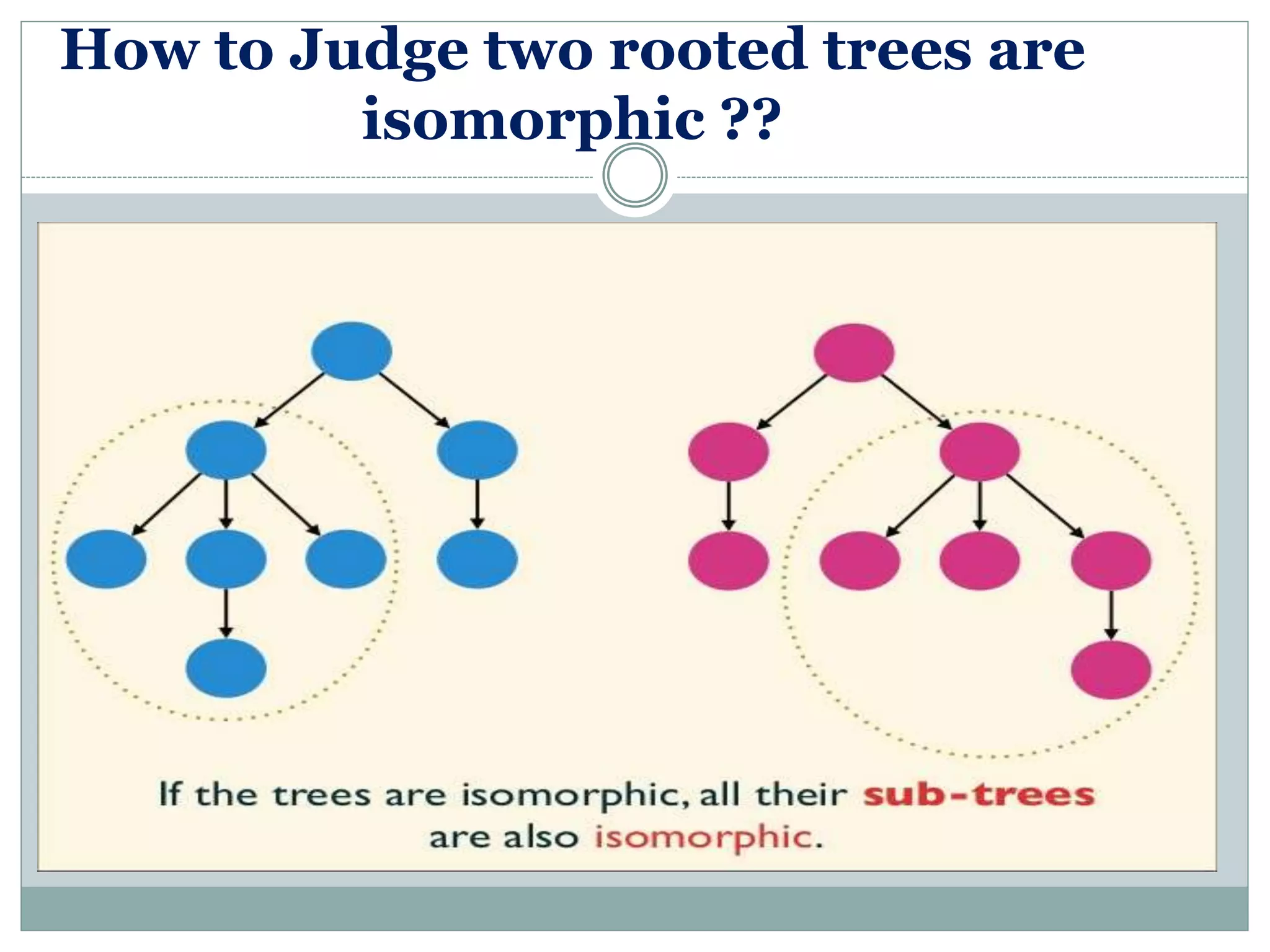
Introduction to methods for determining if two rooted trees are isomorphic.
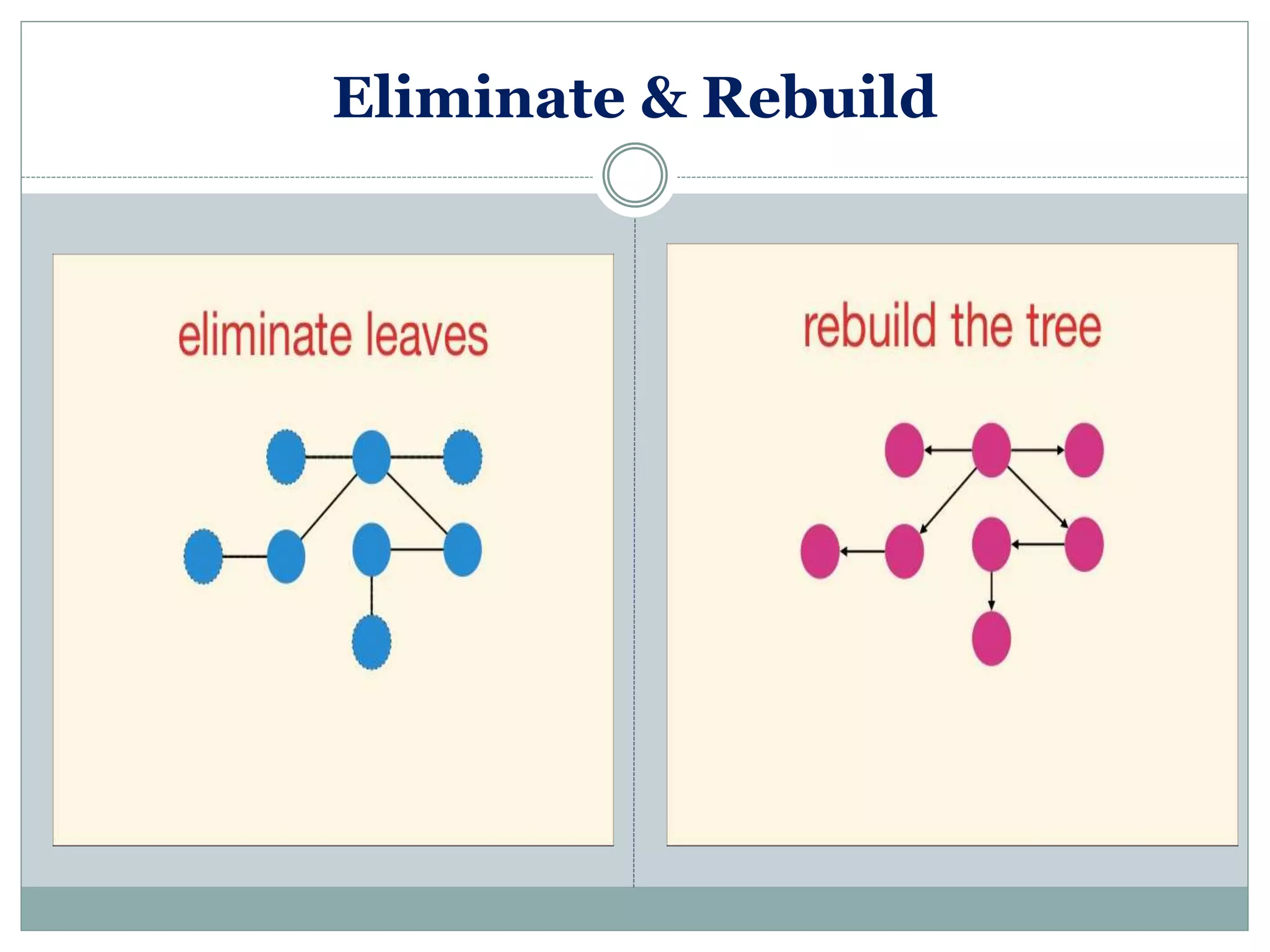
Description of the process of eliminating and rebuilding trees to check for isomorphism.
Closing remarks and thanks for the audience.









