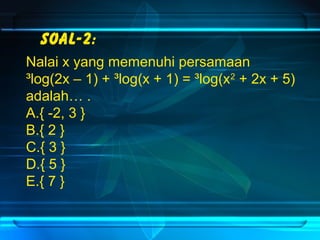
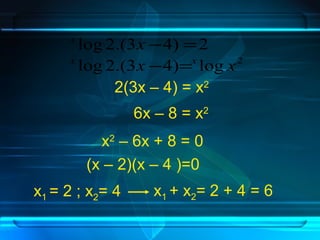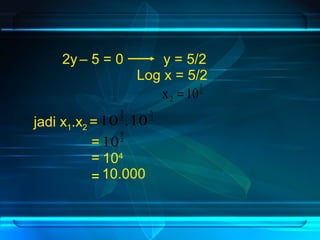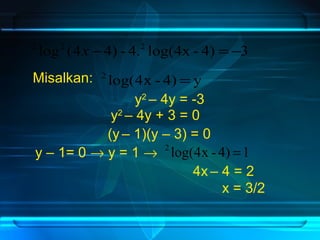Dokumen ini membahas tentang penyelesaian berbagai bentuk persamaan logaritma dan cara mengubahnya menjadi bentuk kuadrat. Beberapa contoh soal dan solusi disertakan untuk menunjukkan langkah-langkah dalam menyelesaikan persamaan logaritma. Selain itu, terdapat penjelasan mengenai kondisi yang diperlukan untuk menyelesaikan persamaan logaritma.

2. Kemampuan yang akan dibahas
Menyelesaikan berbagai bentuk
persamaan logaritma

3. Persamaan Logaritma
Persamaan logaritma dalam x
adalah persamaan yang memuat fungsi x
sebagai numerus atau bilangan pokoknya
Contoh: 1. 3 log(x + 2)=3 log 4
2.2 log(2x -1)=2 log(x +4)
3.
x log 2+x log(3x -4) =2

4. Bentuk persamaan logaritma
1.
2.
3.
a log f (x)=a logb
a log f (x)=a log g(x)
Persamaan logaritma yang diubah
ke bentuk kuadrat

5. 1.Bentuk:
a log f (x)=a log p
maka f(x) = p
asalkan a > 0, a ¹ 1
dan p > 0

6. Soal-1:
Jika 3log (x2 + 1) = 3log 5 maka x
sama dengan… .
A.1
B.2
C.3
D.± 2
E.± 3

7. Jawab:
3log (x2 + 1) = 3log 5
® x2 + 1 = 5
® x2 + 1 – 5 = 0
® x2 – 4 = 0
® (x + 2)(x – 2 ) = 0
® x1 = - 2 atau x2 = 2
Jawab: D

8. Soal-2:
Persamaan
x log 2+x log(3x -4) =2
mempunyai dua penyelesaian,
yaitu x1 dan x2. Harga x1 + x2 =….
Jawab: x log 2+x log(3x -4) =2
x log 2.(3x -4) =2

9. x log 2.(3x -4) =2
x log 2.(3x -4)=x log x2
2(3x – 4) = x2
6x – 8 = x2
x2 – 6x + 8 = 0
(x – 2)(x – 4 )=0
x1 = 2 ; x2= 4 x1 + x2= 2 + 4 = 6

10. 2.Bentuk:
a log f (x)=a log g(x)
maka f(x) = g(x)
asalkan a > 0; a¹ 1;
f(x) > 0 dan g(x) > 0

11. Soal-1:
3log(x2 + 1) . 5log 3 = 5log(x + 21)
apabila x = … .
A.3
B.4
C.5
D.-5 atau 4
E.-4 atau 5

12. Jawab:
3log(x2 + 1) . 5log 3 = 5log(x + 21)
5log 3 .3log(x2 + 1) = 5log(x + 21)
5log(x2 + 1) = 5log(x + 21)
® x2 + 1 = x + 21
® x2 – x – 20 = 0
® (x + 4)(x – 5) = 0
x = –4 atau x = 5 ® jawab: E

13. Soal-2:
Nalai x yang memenuhi persamaan
³log(2x – 1) + ³log(x + 1) = ³log(x2 + 2x + 5)
adalah… .
A.{ -2, 3 }
B.{ 2 }
C.{ 3 }
D.{ 5 }
E.{ 7 }

14. Jawab-2:
³log(2x – 1) + ³log(x + 1) = ³log(x2 + 2x + 5)
³log(2x – 1)(x + 1) = ³log(x2 + 2x + 5)
³log(2x2 + x – 1) = ³log(x2 + 2x + 5)
® 2x2 + x – 1 = x2 + 2x + 5
® x2 – x – 6 = 0
® (x + 2)(x – 3) = 0 ® x = -2 atau x = 3
Nilai x yang memenuhi adalah { 3 }
® jawab: C

15. Persamaan logaritma yang diubah
ke bentuk kuadrat
3.
A(a log x)2 +B(a log x)+C =0
Merupakan persamaan logaritma
yang di ubah ke bentuk persamaan
kuadrat dalam y, yaitu: Ay2 + By + C = 0.
Nilai x dapat ditentukan dengan terlebih
dahulu menentukan nilai y

16. Soal -1:
Jika xdan xadalah akar-akar
1 2 persamaan (3 log x)2 -33 logx + 2 = 0
maka x1.x2 =….
(3 log x)2 -33 logx +2 = 0
Jawab:
Misalkan:
3 log x = y
y2 – 3y + 2 = 0
(y – 1)(y – 2 ) = 0

17. (y – 1)(y – 2 ) = 0
y – 1= 0 ® y = 1 ® 3 log x =1
x1 = 3
y – 2= 0 ® y = 2 ® 3 log x =2
x = 32
x2 = 9
Jadi x1.x2 = 3.9 = 27

18. Soal-2:
Persamaan
mempunyai penyelesaian x1 dan x2.
Hasil kali x1.x2 =….
4(4 -log x)logx =15
( 16 -4 log x )logx = 15
16log x -4(log x)2 =15
-4(log x)2 +16(log x) -15 = 0
Jawab:
4(4-log x)logx =15

19. -4(log x)2 +16(log x)-15 =0
4(log x)2 -16(log x)+15 =0
Misalkan: log x =y
4y2 – 16y + 15) = 0
(2y – 3)(2y - 5) = 0
2y – 3 = 0 y = 3/2
Log x = 3/2
2 3
x 10 1 =

20. 2y – 5 = 0 y = 5/2
Log x = 5/2
x 105 2 =
2
5
2 3 10 . 10
jadi x1.x2 = 2
8 = 10
2
104
10.000
= =

21. Soal-3:
8 1
Nilai x yang memenuhi
2 log2 (4x - 4) -2 log(4x - 4)4=2 log
Jawab:
adalah….
2 log2 (4x -4) -2 log(4x - 4)4=2 log
2 log2 (4x - 4) -42 log(4x - 4)=2 log 2-3
2 log2 (4x -4) - 4.2 log(4x - 4) = -3
8 1

22. 2 log2 (4x -4) - 4.2 log(4x - 4) =-3
Misalkan:
2 log(4x - 4) = y
y2 – 4y = -3
y2 – 4y + 3 = 0
(y – 1)(y – 3) = 0
2 log(4x - 4) =1
y – 1= 0 ® y = 1 ®
4x – 4 = 2
x = 3/2

23. y – 3= 0 ® y = 3 ® 2 log(4x - 4) = 3
4x – 4 = 23
4x – 4 = 8
4x = 12
x= 3
2
jadi x1 = 3/2 atau x2 = 3

25. Jika x1 dan x2 adalah akar-akar persamaan
(log x)2 - 4(log x) + 3 = 0 , maka x1.x2 = ….
A.100
B.1000
C.10000