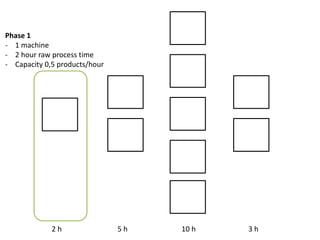
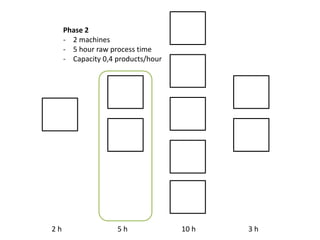
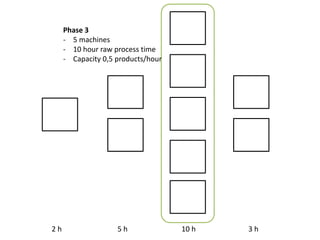
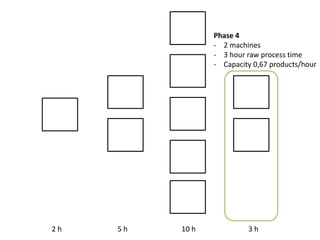
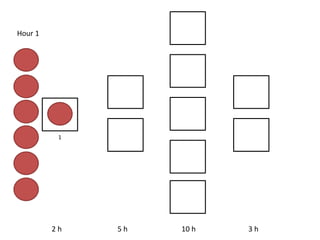
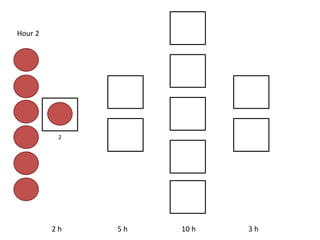
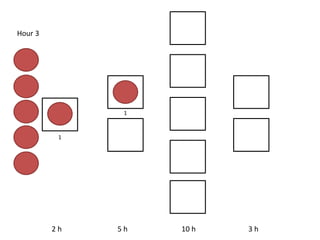
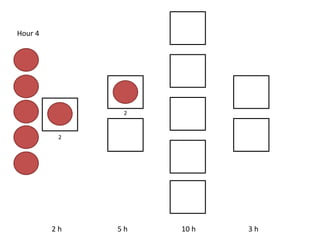
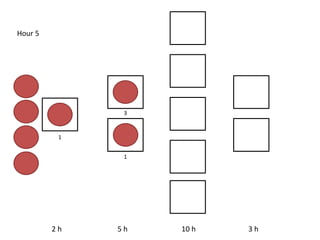
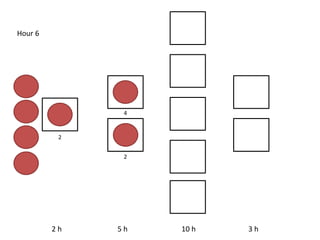
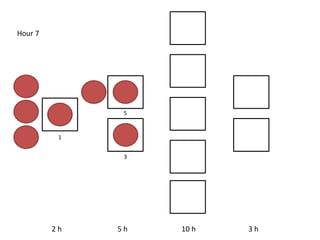
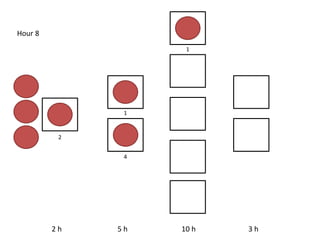
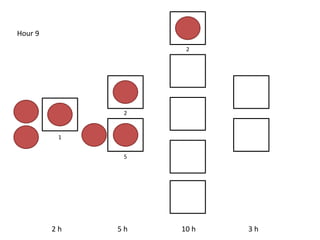
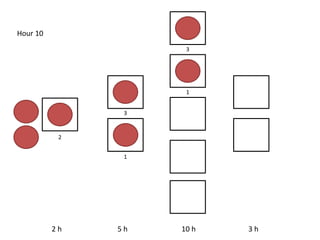
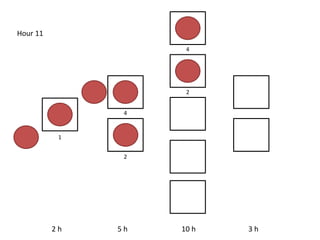
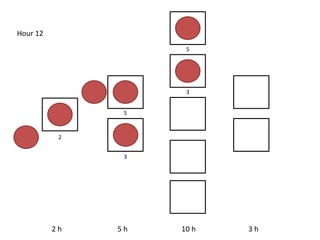
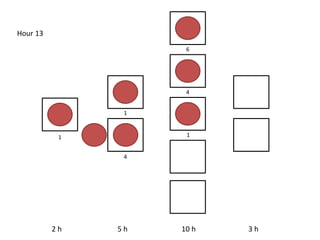
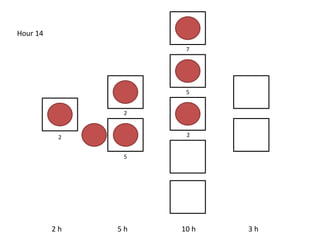
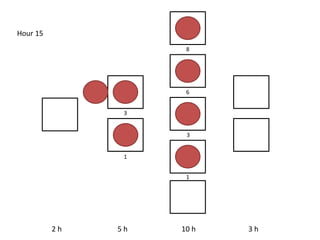
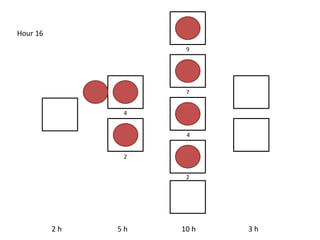
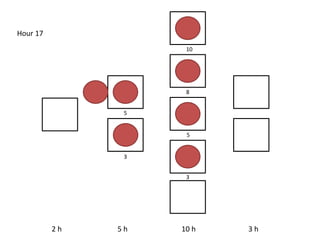
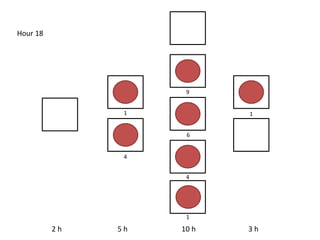
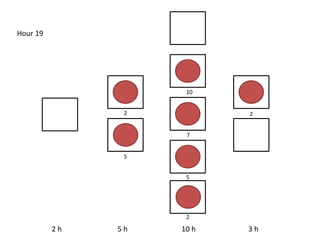
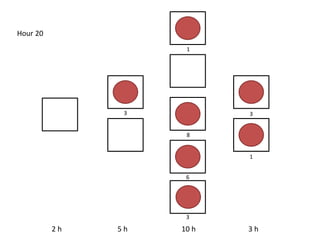
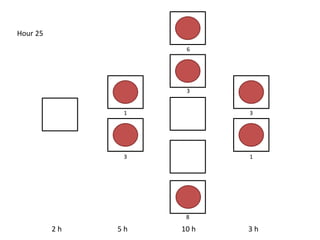
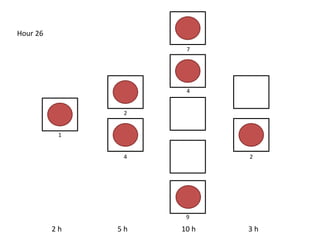
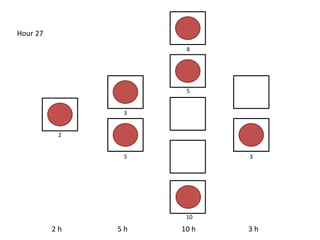
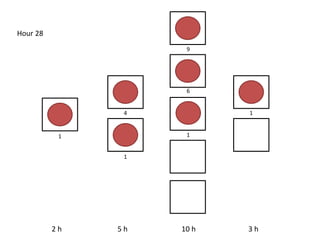
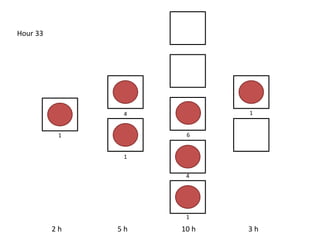
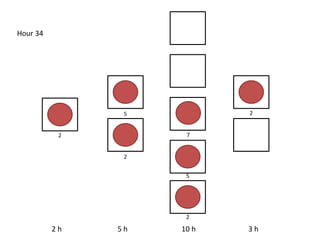
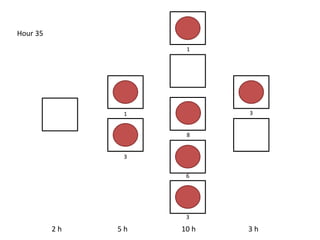
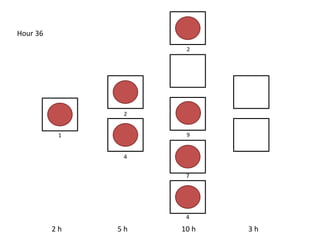
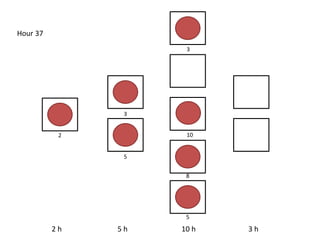
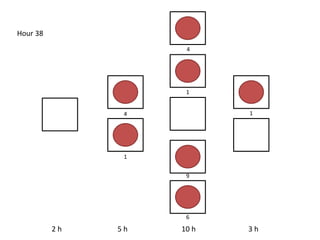
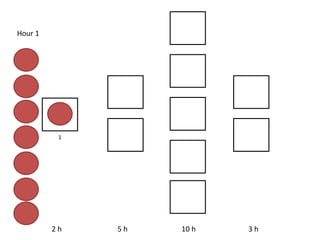
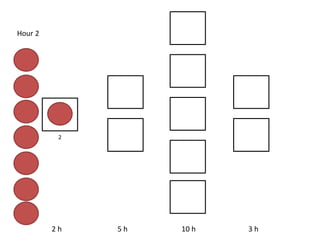
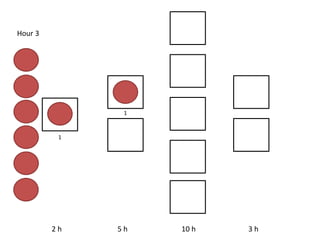
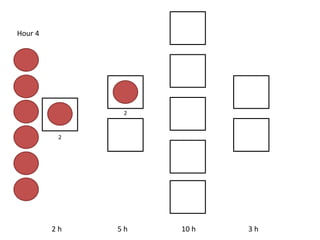
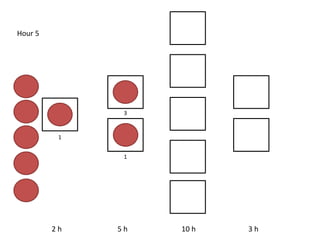
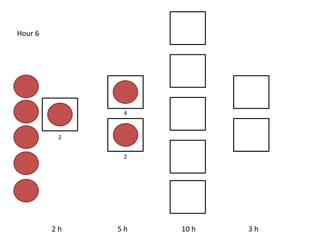
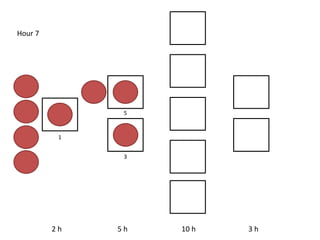
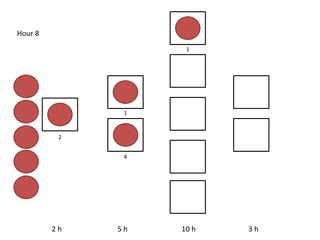
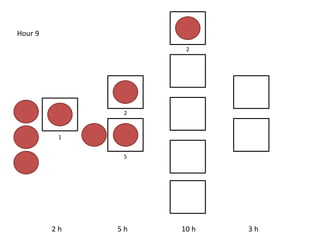
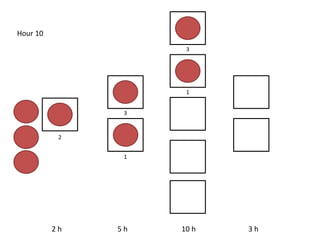
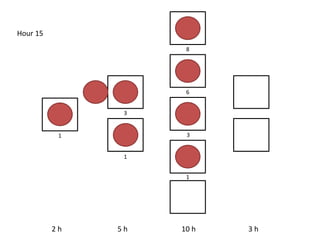
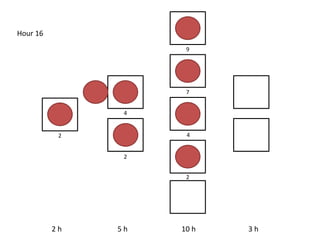
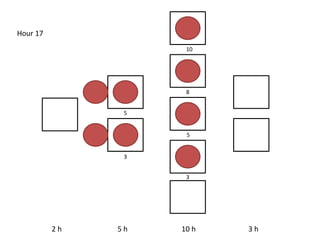
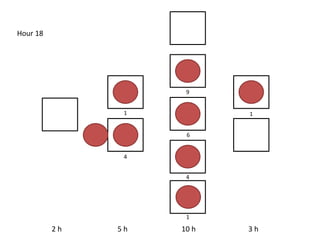
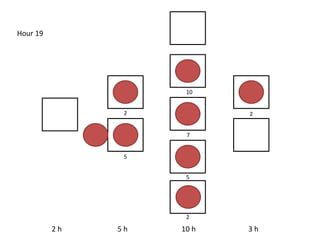
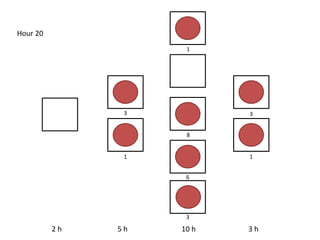
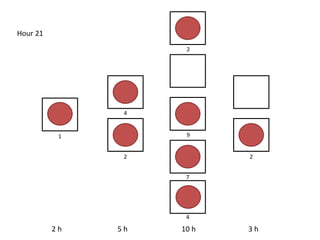
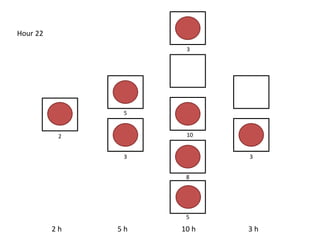
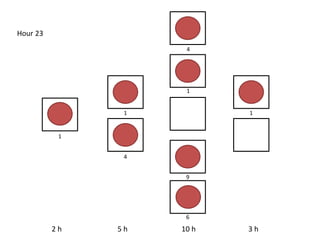
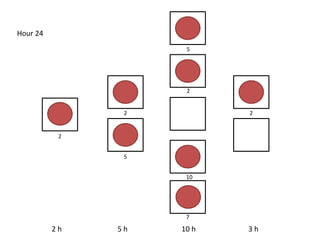
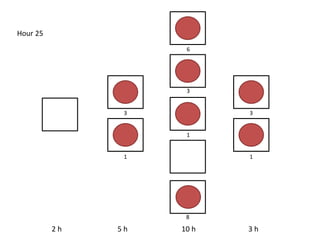
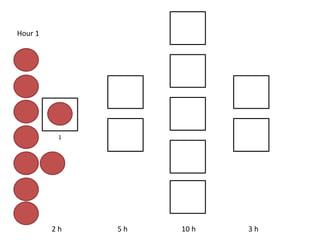
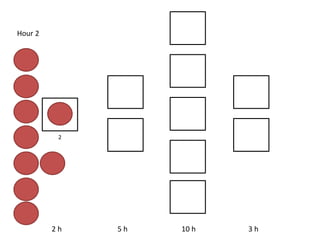
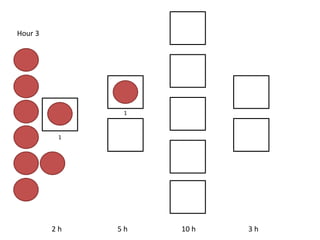
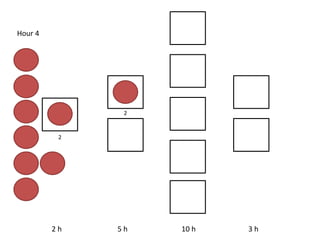
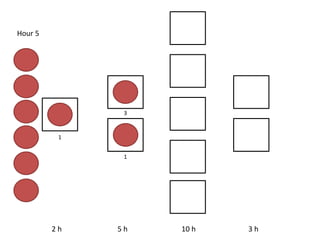
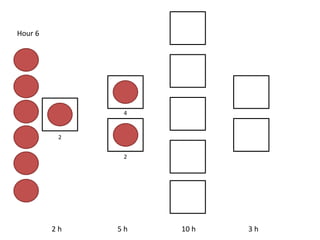
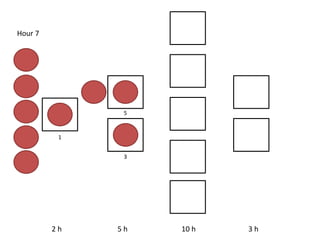
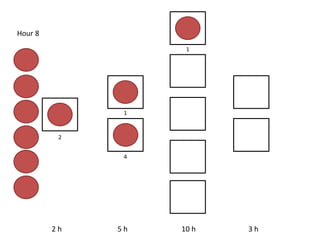
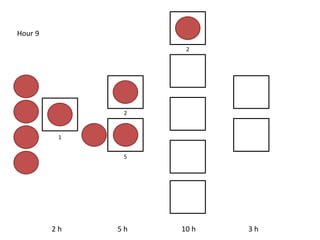
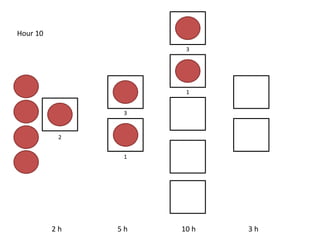
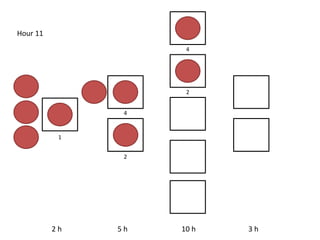
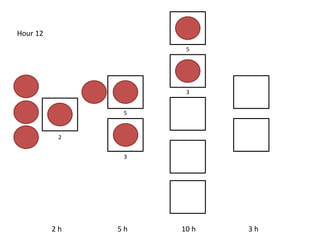
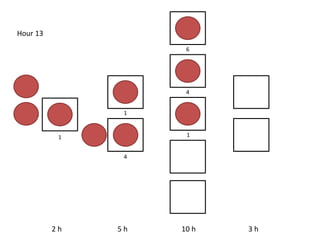
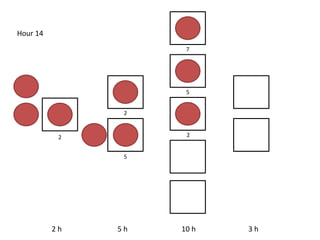
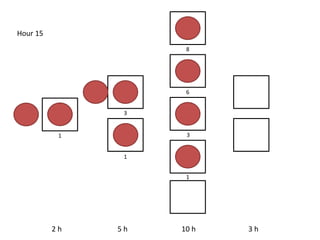
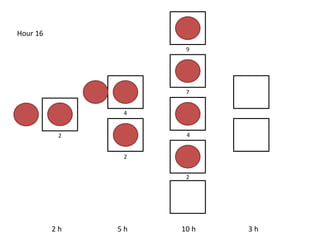
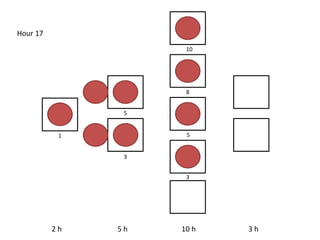
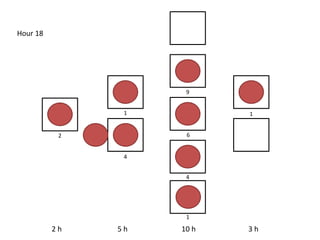
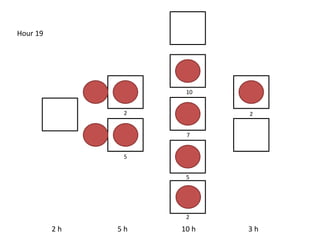
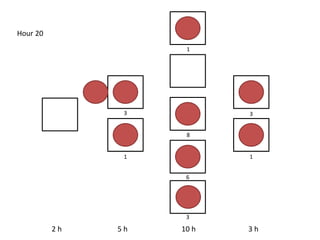
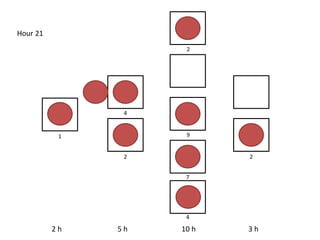
The document outlines a simulation of a production line with varying Work In Progress (WIP) limits of 7, 8, and 9 jobs across three phases, analyzing its impact on job processing and cycle times. It concludes that a WIP limit of 8 jobs allows for full utilization of machines in phase 2 without any queue, achieving optimal performance with a cycle time equal to the raw process time of 20 hours. The findings suggest that for a perfect line with no variability, a WIP limit of 8 jobs maximizes throughput while minimizing WIP and cycle time.

1. WIP controlling - Example line
Unbalanced line
Jesse Uitto

2. Unbalanced line simulation
• Source: Factory Physics by Wallace Hopp &
Mark Spearman - Chapter 7, Intuition building
exercise 1
• Unlike in the book, in this example there is
only 5, not 6, machines in the third phase.
• More about the theory can be found at
http://jesseuitto.fi/?p=464 (example line 2)

3. 2 h 5 h 10 h 3 h
Phase 1
- 1 machine
- 2 hour raw process time
- Capacity 0,5 products/hour

4. 2 h 5 h 10 h 3 h
Phase 2
- 2 machines
- 5 hour raw process time
- Capacity 0,4 products/hour

5. 2 h 5 h 10 h 3 h
Phase 3
- 5 machines
- 10 hour raw process time
- Capacity 0,5 products/hour

6. 2 h 5 h 10 h 3 h
Phase 4
- 2 machines
- 3 hour raw process time
- Capacity 0,67 products/hour

7. Experiment #1
• First we try this line with WIP limit of 7 jobs
• Red balls are jobs
• Each slide simulates the beginning of that
particular hour.
– Example at the beginning of the hour 1 first job is
released and it is finished when hour 2 changes
into hour 3 (slide = hour 3)
– The number below each work station tells what
process hour is going with that part.

8. 2 h 5 h 10 h 3 h
Hour 1
1

9. 2 h 5 h 10 h 3 h
Hour 2
2

10. 2 h 5 h 10 h 3 h
Hour 3
1
1

11. 2 h 5 h 10 h 3 h
Hour 4
2
2

12. 2 h 5 h 10 h 3 h
Hour 5
1
3
1

13. 2 h 5 h 10 h 3 h
Hour 6
2
4
2

14. 2 h 5 h 10 h 3 h
Hour 7
1
5
3

15. 2 h 5 h 10 h 3 h
Hour 8
2
1
4
1

16. 2 h 5 h 10 h 3 h
Hour 9
1
2
5
2

17. 2 h 5 h 10 h 3 h
Hour 10
2
3
1
3
1

18. 2 h 5 h 10 h 3 h
Hour 11
1
4
2
4
2

19. 2 h 5 h 10 h 3 h
Hour 12
2
5
3
5
3

20. 2 h 5 h 10 h 3 h
Hour 13
1
1
4
6
4
1

21. 2 h 5 h 10 h 3 h
Hour 14
2
2
5
7
5
2

22. 2 h 5 h 10 h 3 h
Hour 15
3
1
8
6
3
1

23. 2 h 5 h 10 h 3 h
Hour 16
4
2
9
7
4
2

24. 2 h 5 h 10 h 3 h
Hour 17
5
3
10
8
5
3

25. 2 h 5 h 10 h 3 h
Hour 18
1
4
9
6
4
1
1

26. 2 h 5 h 10 h 3 h
Hour 19
2
5
10
7
5
2
2

27. 2 h 5 h 10 h 3 h
Hour 20
3
8
6
3
3
1
1

28. 2 h 5 h 10 h 3 h
Hour 21
4
9
7
4
2
2
1

29. 2 h 5 h 10 h 3 h
Hour 22
5
10
8
5
3
3
2

30. 2 h 5 h 10 h 3 h
Hour 23
1
9
6
4
1
1
1

31. 2 h 5 h 10 h 3 h
Hour 24
2
10
7
5
2
2
2

32. 2 h 5 h 10 h 3 h
Hour 25
3 1
8
6
1 3
3

33. 2 h 5 h 10 h 3 h
Hour 26
4 2
9
7
2
1
4

34. 2 h 5 h 10 h 3 h
Hour 27
5 3
10
8
3
2
5

35. 2 h 5 h 10 h 3 h
Hour 28
1
1
1
9
4
1
6

36. 2 h 5 h 10 h 3 h
Hour 29
2
2
2
10
5
2
7

37. 2 h 5 h 10 h 3 h
Hour 30
3
1 3
1
1
3
8

38. 2 h 5 h 10 h 3 h
Hour 31
4
2
1
2
2
4
9

39. 2 h 5 h 10 h 3 h
Hour 32
5
3
2
3
3
5
10

40. 2 h 5 h 10 h 3 h
Hour 33
1
4
1
1
4
6
1

41. 2 h 5 h 10 h 3 h
Hour 34
2
5
2
2
5
7
2

42. 2 h 5 h 10 h 3 h
Hour 35
3
1
3
1
6
8
3

43. 2 h 5 h 10 h 3 h
Hour 36
4
2
4
2
7
91

44. 2 h 5 h 10 h 3 h
Hour 37
5
3
5
3
8
102

45. 2 h 5 h 10 h 3 h
Hour 38
1
4
6
4
9
1
1

46. Notices of simulation with WIP = 7
• This hour 38 is exactly the same as hour 18 so
it starts to go round between hours 18 -> 37
• Notice that after the beginning there is no
queue in front of the phase 2.
– Actually during the hours 20-24 both stations at
phase 2 aren’t even fully utilized.
– Bottleneck station should be fully utilized, right ?
• So let’s try this with an WIP level of 8 jobs

47. 2 h 5 h 10 h 3 h
Hour 1
1

48. 2 h 5 h 10 h 3 h
Hour 2
2

49. 2 h 5 h 10 h 3 h
Hour 3
1
1

50. 2 h 5 h 10 h 3 h
Hour 4
2
2

51. 2 h 5 h 10 h 3 h
Hour 5
1
3
1

52. 2 h 5 h 10 h 3 h
Hour 6
2
4
2

53. 2 h 5 h 10 h 3 h
Hour 7
1
5
3

54. 2 h 5 h 10 h 3 h
Hour 8
2
1
4
1

55. 2 h 5 h 10 h 3 h
Hour 9
1
2
5
2

56. 2 h 5 h 10 h 3 h
Hour 10
2
3
1
3
1

57. 2 h 5 h 10 h 3 h
Hour 11
1
4
2
4
2

58. 2 h 5 h 10 h 3 h
Hour 12
2
5
3
5
3

59. 2 h 5 h 10 h 3 h
Hour 13
1
1
4
6
4
1

60. 2 h 5 h 10 h 3 h
Hour 14
2
2
5
7
5
2

61. 2 h 5 h 10 h 3 h
Hour 15
3
1
8
6
3
1
1

62. 2 h 5 h 10 h 3 h
Hour 16
4
2
9
7
4
2
2

63. 2 h 5 h 10 h 3 h
Hour 17
5
3
10
8
5
3

64. 2 h 5 h 10 h 3 h
Hour 18
1
4
9
6
4
1
1

65. 2 h 5 h 10 h 3 h
Hour 19
2
5
10
7
5
2
2

66. 2 h 5 h 10 h 3 h
Hour 20
3
8
6
3
3
1
11

67. 2 h 5 h 10 h 3 h
Hour 21
4
9
7
4
2
2
1
2

68. 2 h 5 h 10 h 3 h
Hour 22
5
10
8
5
3
3
2
3

69. 2 h 5 h 10 h 3 h
Hour 23
4
9
6
4
1
1
1
1

70. 2 h 5 h 10 h 3 h
Hour 24
5
10
7
5
2
2
2
2

71. 2 h 5 h 10 h 3 h
Hour 25
1 1
8
6
3 3
3
1

72. Notices of simulation with WIP = 8
• This hour 25 is exactly the same as hour 20 so
it starts to go round between hours 20 – 24
• So after the start there is no queue in front of
the second phase. But it’s still fully utilized.
– Bottleneck stations are fully utilized, so this is the
best solution?
• Let’s try this once again with WIP limit of 9
jobs

73. 2 h 5 h 10 h 3 h
Hour 1
1

74. 2 h 5 h 10 h 3 h
Hour 2
2

75. 2 h 5 h 10 h 3 h
Hour 3
1
1

76. 2 h 5 h 10 h 3 h
Hour 4
2
2

77. 2 h 5 h 10 h 3 h
Hour 5
1
3
1

78. 2 h 5 h 10 h 3 h
Hour 6
2
4
2

79. 2 h 5 h 10 h 3 h
Hour 7
1
5
3

80. 2 h 5 h 10 h 3 h
Hour 8
2
1
4
1

81. 2 h 5 h 10 h 3 h
Hour 9
1
2
5
2

82. 2 h 5 h 10 h 3 h
Hour 10
2
3
1
3
1

83. 2 h 5 h 10 h 3 h
Hour 11
1
4
2
4
2

84. 2 h 5 h 10 h 3 h
Hour 12
2
5
3
5
3

85. 2 h 5 h 10 h 3 h
Hour 13
1
1
4
6
4
1

86. 2 h 5 h 10 h 3 h
Hour 14
2
2
5
7
5
2

87. 2 h 5 h 10 h 3 h
Hour 15
3
1
8
6
3
1
1

88. 2 h 5 h 10 h 3 h
Hour 16
4
2
9
7
4
2
2

89. 2 h 5 h 10 h 3 h
Hour 17
5
3
10
8
5
3
1

90. 2 h 5 h 10 h 3 h
Hour 18
1
4
9
6
4
1
1
2

91. 2 h 5 h 10 h 3 h
Hour 19
2
5
10
7
5
2
2

92. 2 h 5 h 10 h 3 h
Hour 20
3
8
6
3
3
1
11

93. 2 h 5 h 10 h 3 h
Hour 21
4
9
7
4
2
2
1
2

94. 2 h 5 h 10 h 3 h
Hour 22
5
10
8
5
3
3
2
3

95. 2 h 5 h 10 h 3 h
Hour 23
4
9
6
4
1
1
1
1

96. 2 h 5 h 10 h 3 h
Hour 24
5
10
7
5
2
2
2
2

97. 2 h 5 h 10 h 3 h
Hour 25
1 1
8
6
3 3
3
1

98. Notices of simulation with WIP = 9
• Notice that here too hour 25 is same than
hour 20. So it goes same round than with WIP
of 8 jobs
• Now after the start there is always 1 job in
queue waiting to be processed at the second
phase

99. Variability at the phase 2
• If process time at the second phase would be
shorter they could take a new job from the
queue. On the other hand it would mean that
stations have variability and they would also
have longer process times which would
increase the queue.

100. Differences
• With WIP limit of 7 second work phase
sometimes starves and is not fully utilized. So the
cycle time for the line is same as theoretical raw
process time T0 = 20 h
• With second example and WIP limit of 8 jobs the
second phase is always fully utilized. And still
there is no queue in front of it. So the cycle time
still remains at 20 hours.
• With the WIP of 9 jobs there is always queue in
front of the second phase. After the start when
all the WIP is in use, jobs will wait 2 hours to get
processed at the phase 2.
– So the cycle time is 22 hours

101. Summarize
• As calculated in post (http://jesseuitto.fi/?p=464) Critical
WIP is W0 = rb* T0 = 0,4 * 20 = 8 jobs
– In simulations we noticed that line works quite
perfectly with this WIP limit.
• Machines at second phase are fully utilized
• No queues in the line
• Cycle time = raw process time T0
• So if we have perfect line with no variability,
no loss, optimum situation would be to limit
the WIP for 8 jobs
– Achieve maximum TH with minimum WIP and CT