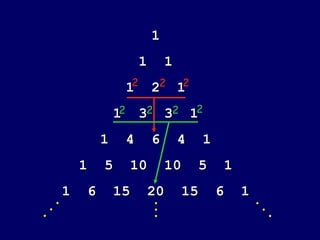
The document discusses different types of pizzas that can be ordered based on the number of available toppings. It notes that with 8 total toppings, you can order: 1) A plain pizza with no toppings 2) A pizza with all 8 toppings 3) The number of possible pizzas with 1 topping or 7 toppings is 8, as calculated by the binomial coefficient formula.

1. “ Pascal’s Triangle” Al-Karaji, Baghdad 953-1029 Chu Shin-Chieh 1303 The Precious Mirror of the Four Elements . . . Known in Europe by 1529 Blaise Pascal 1654

2. The Binomial Formula (1+X) 1 = (1+X) 0 = (1+X) 2 = (1+X) 3 = 1 1 + 1 X 1 + 2 X + 1 X 2 1 + 3 X + 3 X 2 + 1 X 3 (1+X) 4 = 1 + 4 X + 6 X 2 + 4 X 3 + 1 X 4

3. Pascal’s Triangle: k th row are the coefficients of (1+X) k (1+X) 1 = (1+X) 0 = (1+X) 2 = (1+X) 3 = 1 1 + 1 X 1 + 2 X + 1 X 2 1 + 3 X + 3 X 2 + 1 X 3 (1+X) 4 = 1 + 4 X + 6 X 2 + 4 X 3 + 1 X 4

4. Summing The Rows 1 1 + 1 1 + 2 + 1 1 + 3 + 3 + 1 1 + 4 + 6 + 4 + 1 1 + 5 + 10 + 10 + 5 + 1 1 + 6 + 15 + 20 + 15 + 6 + 1 =1 =2 =4 =8 =16 =32 =64

5. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 6+20+6 1+15+15+1 =

6. Summing on 1 st Avenue 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1

7. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 Summing on k th Avenue

8. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 2 2 2 2 2 2 2

9. 1 1 1 1 2 1 1 3 3 1 1 4 6 4 1 1 5 10 10 5 1 1 6 15 20 15 6 1 =2 =5 =13 =3 =8

11. The product of the numbers in the yellow petals is 5 x 20 x 21 = 2100. The product of the numbers in the orange petals is 6 x 10 x 35 = 2100.

12. 5 x 21 x 20 = 5 x 7 x 3 x 2 x 2 x 5 = 5^2 x 2^2 x 3 x 5 10 x 6 x 35 = 5 x 2 x 3 x 2 x 7 x5 = 5^2 x 2^2 x 3 x 5

13. It's Friday night and the Pizza Palace is more crowded than usual. At the counter the Pascalini's are trying to order a large pizza, but can't agree on what topping(s) to select.Antonio, behind the counter, says, "I only have 8 different toppings. It can't be that hard to make up your mind. How many different pizzas could that be?" "Well, we could get a plain pizza with no toppings," says Mr. Pascalini. "Or we could get a pizza with all 8 toppings," says Mrs. Pascalini. "What about a pizza with extra cheese and green peppers?" asks Pepe. "You're not helping!" Antonio yells at Pepe. "Get back to work." As Pepe starts to clear off the nearest table, he mumbles to himself, "or a pizza with anchovies, extra cheese, mushrooms, and olives." Antonio hands an order pad to Mr. Pascalini and says, "When you decide, write it down and I'll make it." Then he helps the next people in line, who know what they want: a large pizza with mushrooms, green peppers and tomatoes.

14. It's Friday night and the Pizza Palace is more crowded than usual. At the counter the Pascalini's are trying to order a large pizza, but can't agree on what topping(s) to select.Antonio, behind the counter, says, "I only have 8 different toppings. It can't be that hard to make up your mind. How many different pizzas could that be?" "Well, we could get a plain pizza with no toppings," says Mr. Pascalini. "Or we could get a pizza with all 8 toppings," says Mrs. Pascalini. "What about a pizza with extra cheese and green peppers?" asks Pepe. "You're not helping!" Antonio yells at Pepe. "Get back to work." As Pepe starts to clear off the nearest table, he mumbles to himself, "or a pizza with anchovies, extra cheese, mushrooms, and olives." Antonio hands an order pad to Mr. Pascalini and says, "When you decide, write it down and I'll make it." Then he helps the next people in line, who know what they want: a large pizza with mushrooms, green peppers and tomatoes. How many different pizzas can you order with only one topping?

15. It's Friday night and the Pizza Palace is more crowded than usual. At the counter the Pascalini's are trying to order a large pizza, but can't agree on what topping(s) to select.Antonio, behind the counter, says, "I only have 8 different toppings. It can't be that hard to make up your mind. How many different pizzas could that be?" "Well, we could get a plain pizza with no toppings," says Mr. Pascalini. "Or we could get a pizza with all 8 toppings," says Mrs. Pascalini. "What about a pizza with extra cheese and green peppers?" asks Pepe. "You're not helping!" Antonio yells at Pepe. "Get back to work." As Pepe starts to clear off the nearest table, he mumbles to himself, "or a pizza with anchovies, extra cheese, mushrooms, and olives." Antonio hands an order pad to Mr. Pascalini and says, "When you decide, write it down and I'll make it." Then he helps the next people in line, who know what they want: a large pizza with mushrooms, green peppers and tomatoes. How many different pizzas can you order with only one topping? How many different pizzas can you order each with seven toppings?

16. 8 : 1 8 : 7

17. When you order a 1-topping pizza, you choose not to use 7 toppings. When you order a 7-topping pizza, you choose not to use 1 topping. The number of total possible choices is the same in each case: 8.

18. 8 : 1 8 : 7 n! [n:k] = -------- k! (n-k)!