Downloaded 48 times
Uploaded byAnnisa Khoerunnisya
Pasang surut
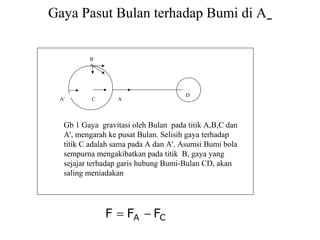
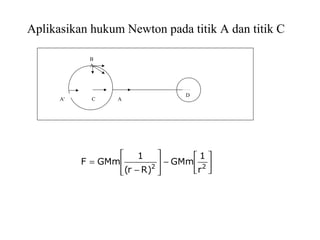
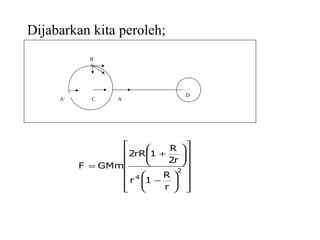
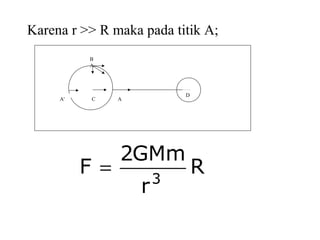
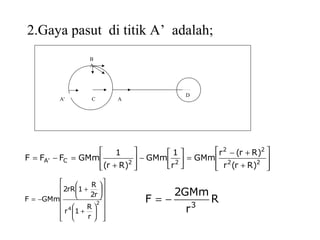
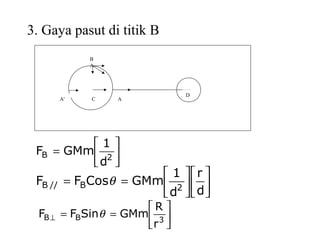
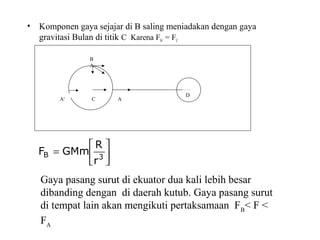
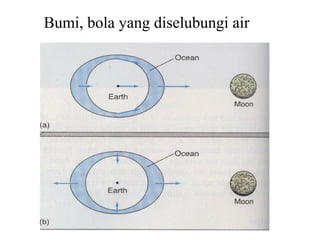
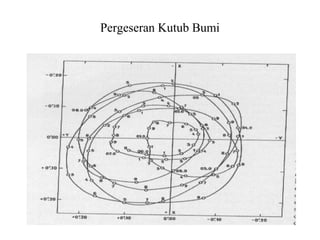
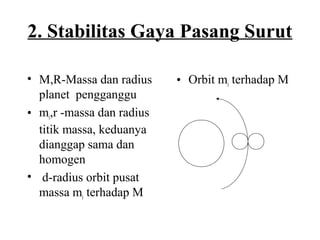
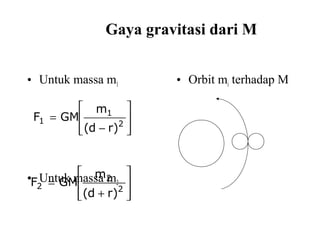
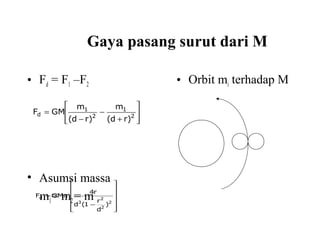
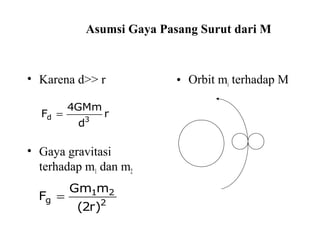
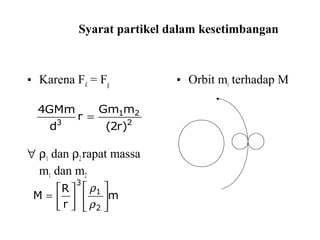
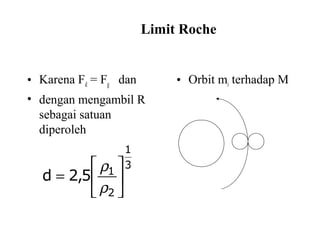
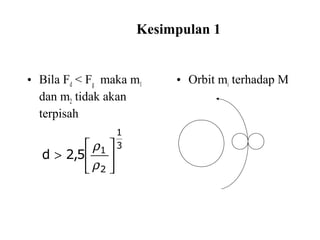
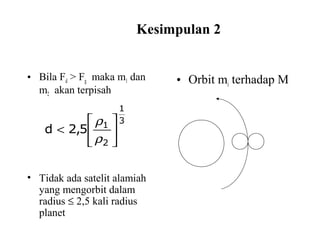
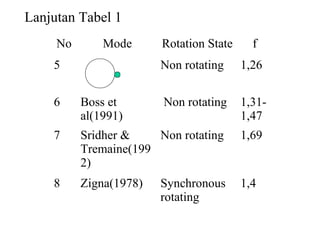
Dokumen ini membahas tentang gaya pasang surut yang disebabkan oleh interaksi gravitasi antara Bumi, bulan, dan matahari. Pasang surut dipengaruhi oleh berbagai faktor termasuk posisi benda langit, geografi, dan kondisi dasar laut. Selain itu, dijelaskan juga konsep 'harbor time' dan dampak perubahan rotasi Bumi akibat gesekan antara air laut dan dasar laut.
More Related Content
Pasang surut
- 1. 1. Gaya PasangSurut Yang dimaksud dengan gaya pasang surut adalah perbedaan gaya pada sebuah titik di permukaan planet dengan gaya yang bekerja pada titik pusat planet.
- 2. Gb 1 Gayagravitasi oleh Bulan pada titik A,B,C dan A', mengarah ke pusat Bulan. Selisih gaya terhadap titik C adalah sama pada A dan A'. Asumsi Bumi bola sempurna mengakibatkan pada titik B, gaya yang sejajar terhadap garis hubung Bumi-Bulan CD, akan saling meniadakan A' B A C A D CA FFF −= Gaya Pasut Bulan terhadap Bumi di A
- 3. A' B A C A D Aplikasikan hukumNewton pada titik A dan titik C − − = 22 r 1 GMm )Rr( 1 GMmF
- 4. A' B A C A D Dijabarkan kitaperoleh; − + = 2 4 r R 1r r2 R 1rR2 GMmF
- 5. A' B A C A D Karena r>> R maka pada titik A; R r GMm2 F 3 =
- 6. A' B A C A D 2.Gaya pasutdi titik A’ adalah; + +− = − + =−= 22 22 22C'A )Rr(r )Rr(r GMm r 1 GMm )Rr( 1 GMmFFF + + −= 2 4 r R 1r r2 R 1rR2 GMmF R r GMm2 F 3 −=
- 7. A' B A C A D 3. Gayapasut di titik B = 2B d 1 GMmF == d r d 1 GMmCosFF 2B//B θ ==⊥ 3BB r R GMmSinFF θ
- 8. A' B A C A D • Komponengaya sejajar di B saling meniadakan dengan gaya gravitasi Bulan di titik C Karena Fb// = FC = 3B r R GMmF Gaya pasang surut di ekuator dua kali lebih besar dibanding dengan di daerah kutub. Gaya pasang surut di tempat lain akan mengikuti pertaksamaan FB < F < FA
- 9. Bumi, bola yangdiselubungi air
- 10. Pasang Purnama (viveeau, spring tides) dan Pasang Purbani (morte eau, neap tide) Gaya pasang surut akan maksimum bila resultante gaya gravitasi Bumi, Bulan dan Matahari terletak pada suatu garis lurus. Keadaan ini berlangsung pada saat bulan purnama atau bulan baru. Naiknya permukaan air laut pada saat ini disebut "pasang purnama". Gaya pasang surut akan minimum apabila gaya gravitasi Bulan dan Matahari saling meniadakan, ini terjadi pada saat Bulan-Bumi-Matahari membentuk sudut 900 Posisi ini disebut Bulan kuartir, terjadi pada saat Bulan berumur sekitar 7 hari dan 21 hari. Naiknya permukaan air laut merupakan tinggi yang minimum. Peristiwa ini disebut "pasang purbani" Arah Matahari (a) (b) (c) 1. Pasang Purnama dan Pasang Purbani
- 11. Pasang-surut(pasut) disuatu tempattidak hanya bergantung pada posisi Bulan dan Matahari saja, tetapi dipengaruhi juga oleh keadaan geografi, gesekan pada dasar laut, kedalaman, relief dasar laut dan viskositas air di lokasi tersebut. Semua faktor ini dapat mempercepat atau memperlambat datangnya air pasang. Perbedaan waktu antara datangnya pasang naik dengan waktu yang dihitung disebut "harbor- time". Sebagai contoh, tanggal 3 April 1950 di Brest, Perancis setelah bulan purnama amplitudo air pasang mencapai 7 meter (vive eau, spring tides, pasang purnama), 7 hari kemudian 10 April 1950 setelah quartier terakhir. Amplitudo gelombang air pasang mencapai 2,5 meter (morte eau, neap tide, pasang purbani). Peristiwa terjadinya pasut tidak selalu cocok jika hanya posisi Bulan yang diperhitungkan. Pasut berlangsung lebih lambat, di Brest terlambat 3 sampai 4 jam setelah Bulan lewat. Untuk pelabuhan Hamburg di Jerman selang waktu ini berkisar antara 5 sampai 6 jam. Selain itu pasang purnama juga tidak berlangsung tepat pada saat syzyg (bulan baru atau bulan purnama) pasut berlangsung 1,5 hari lebih lambat Arah Matahari (a) (b) (c) 2. Harbor Time
- 12.
- 13. Perubahan posisi Bulandan Matahari akan menyebabkan terjadinya gesekan air laut yang mengalir dengan dasar laut, hal ini akan memperlambat rotasi Bumi, akibatnya panjang hari di Bumi akan bertambah sekitar 0,0016 detik/abad. Perhitungan ini didukung oleh fakta peristiwa gerhana yang pernah dicatat oleh orang-orang Babilonia dulu, ternyata perhitungan mundur berdasarkan komputasi astronomi modern, selalu tidak cocok dengan catatan tersebut Arah Matahari (a) (b) (c) 3.Rotasi Bumi menjadi lebih lambat
- 14.
- 15. 2. Stabilitas GayaPasang Surut • M,R-Massa dan radius planet pengganggu • mi,r -massa dan radius titik massa, keduanya dianggap sama dan homogen • d-radius orbit pusat massa mi terhadap M • Orbit mi terhadap M
- 16. Gaya gravitasi dariM • Untuk massa m1 • Untuk massa m2 • Orbit mi terhadap M − = 2 1 1 )rd( m GMF + = 2 2 2 )rd( m GMF
- 17. Gaya pasang surutdari M • Fd = F1 –F2 • Asumsi massa m1= m2= m • Orbit mi terhadap M + − − = 2 1 2 1 d )rd( m )rd( m GMF − = 2 2 2 3 d ) d r 1(d r4 GMmF
- 18. Asumsi Gaya PasangSurut dari M • Karena d>> r • Gaya gravitasi terhadap m1 dan m2 • Orbit mi terhadap M r d GMm4 F 3d = 2 21 g )r2( mGm F =
- 19. Syarat partikel dalamkesetimbangan • Karena Fd = Fg ∀ ρ1 dan ρ2rapat massa m1 dan m2 • Orbit mi terhadap M 2 21 3 )r2( mGm r d GMm4 = m r R M 2 1 3 = ρ ρ
- 20. Limit Roche • KarenaFd = Fg dan • dengan mengambil R sebagai satuan diperoleh • Orbit mi terhadap M 3 1 2 1 5,2d = ρ ρ
- 21. Kesimpulan 1 • BilaFd < Fg maka m1 dan m2 tidak akan terpisah • Orbit mi terhadap M 3 1 2 1 5,2d > ρ ρ
- 22. Kesimpulan 2 • BilaFd > Fg maka m1 dan m2 akan terpisah • Tidak ada satelit alamiah yang mengorbit dalam radius ≤ 2,5 kali radius planet • Orbit mi terhadap M 3 1 2 1 5,2d < ρ ρ
- 23. Bentuk Umum LimitRoche Kondisi berlakunya persamaan diatas; massa homogen, hydrostatic fluid, synchronously co-rotating dalam hal ini, ρp – density planet Rp – jari2 planet r – radius planet ρc – density object sekunder f – konstanta regresi bergantung pada macam model yang dipilih p 3/1 c p Rfr = ρ ρ
- 24. Tabel 1. Konstantaf untuk berbagai model No Mode Rotation State f 1 Hydrostatic fluid Synchronous rotating 2,46 2 Synchronous rotating 2,88 3 Non rotating 2,52 4 Synchronous rotating 1,42
- 25. Lanjutan Tabel 1 NoMode Rotation State f 5 Non rotating 1,26 6 Boss et al(1991) Non rotating 1,31- 1,47 7 Sridher & Tremaine(199 2) Non rotating 1,69 8 Zigna(1978) Synchronous rotating 1,4
- 26. Syarat dan definisi Syarat:Fg + Fps + Fs = 0 dengan Fg – percepatan gravitasi Fps – percepatan pasang surut Fs – percepatan sentrifugal a- radius ekuator benda,ω-frekuensi spin, ω0- frekuensi orbit permukaan ρp– rapat massa planet(Matahari) ρc – rapat massa kritis r - jarak terdekat a/b – rasio sumbu elipsoida
- 27. a). Untuk bolaberotasi “Rubber-Pile” ( percepatan pasang surut) ( percepatan gravitasi) ( percepatan sentrifugal) a r R 2F 3 p p 2 0ps = ρω aF 2 s ω= aF C 2 0g ρω−=
- 28. • Diperoleh • Dalamhal synchronous rotating body 0aa r R 2a 2 3 p p 2 0C 2 0 =+ +− ωρωρω 2 0 3 p p r R = ω ω ρ 2 0 3 p pC r R 2 + = ω ω ρρ
- 29. b)Limit Roche untukelipsoida berotasi “Rubber-Pile” , disrupsi terjadi bila dipenuhi + = b a r R 2 2 0 3 p pC ω ω ρρ
- 30. Untuk P/Shoemaker-Levy 9disrupsi terjadi pada r ≈ 1,3 Rp Merupakan limit atas terjadinya disrupsi, sedangkan untuk non rotating sphere diperoleh ρc ≈ 1,2 tetapi untuk a/b = 2 ρc ≈ 2,4 untuk non rotating body += b a P 3,3 22,1 2 rot h Cρ
- 31.
- 32. Transfer massa, pasanganbinary β Lyrae
- 33. Daftar Bacaan • Boss,A.F., Cameron,A.G.W., ansd Benz.; 1991, "Tidal Disruption Of Inviscid Planetesimals", Icarus,92,165-178 • Chaisson,E and McMillan,S.; 1993 Astronomy Today, Prentice Hall,New Jersey • Danby,J.M.A.; 1988 Fundamentals of Celestial Mechanics, Willmann- Bell,Inc, Richmond, Virginia • Flammarion,G.C et Danjon,A.; 1955 Astronomie Populaire, Flammarion, Paris • Harris,A.W.; 1996 Earth, Moon and Planets,72,112-117 • Sridhar,S., and Tremaine,S.; 1992," Tidal Disruption of Viscous Bodies", Icarus,95,86-99 • Ziglina,I.N.; 1978, " Tidal Disruption of Bodies", Icarus,95,86-99