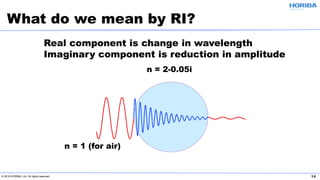
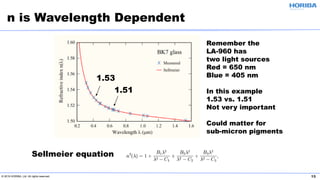
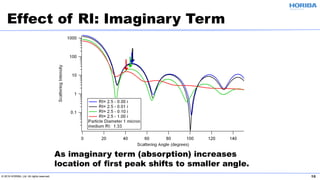
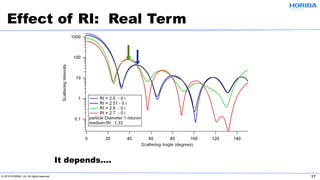
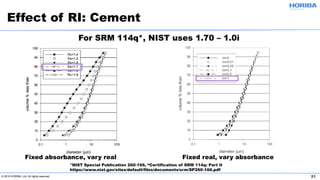
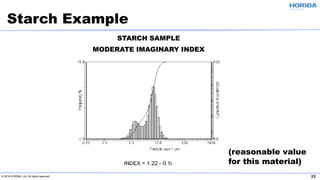
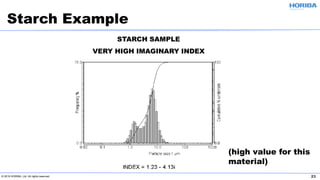
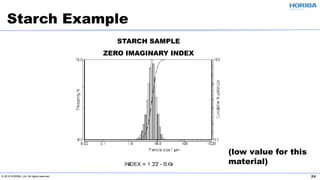
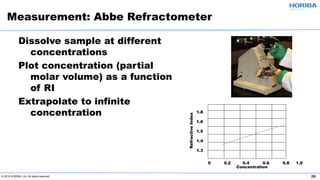
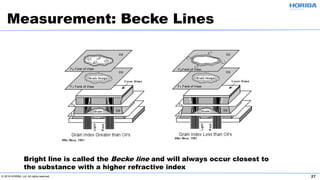
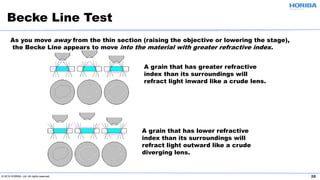
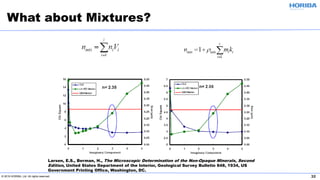
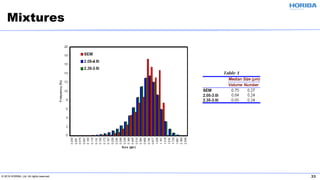
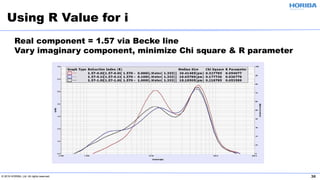
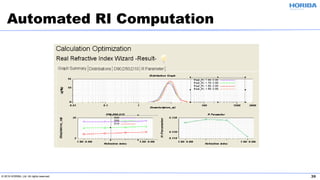
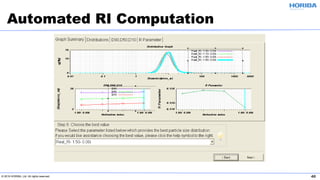
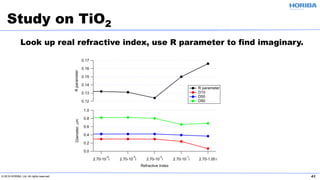
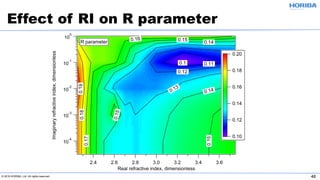
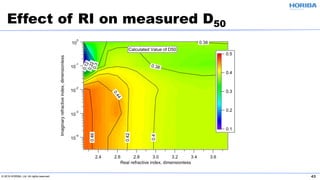
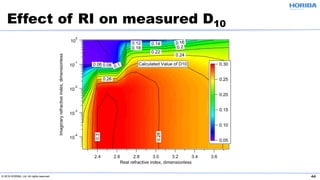
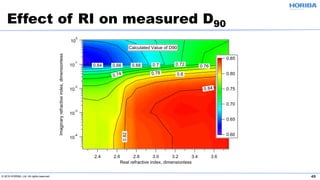
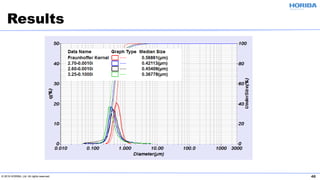
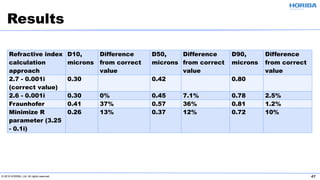
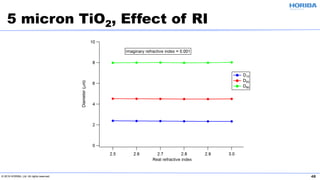
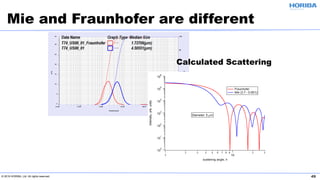
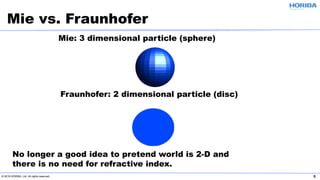
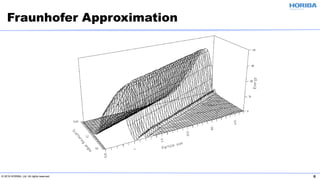
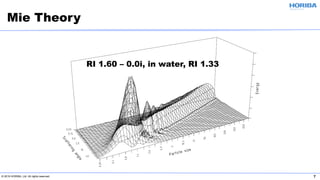
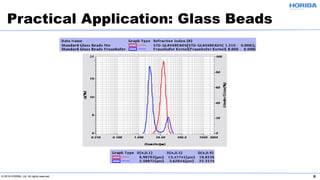
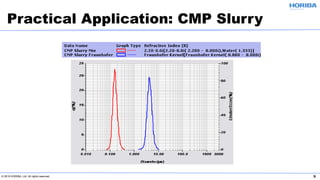
The document discusses the optical properties of particles and the significance of the refractive index (RI) in particle analysis using light scattering techniques, specifically Mie and Fraunhofer theories. It highlights the distinction between real and imaginary components of RI, their definitions, and their practical implications in various particle types and sizes. Furthermore, it provides recommendations for measuring RI effectively and redundantly to minimize errors in particle size analysis.







![© 2019 HORIBA, Ltd. All rights reserved. 13
1 / d = α
k = (λ ⁄ 4 π ) α
Example: for a value of k = 0.1
k = ( λ ⁄ 4 π ) [α] = 0.05 x [1 / d] = 0.1 = k
d = 0.05 / 0.1 = 0.5 micron
RI: Imaginary Component
100%
Intensity
1 / e = 37%
d Distance into medium](https://image.slidesharecdn.com/particleclassroomseriesiii-refractiveindexandlaserdiffraction-190318191047/85/Particle-Classroom-Series-III-Refractive-Index-and-Laser-Diffraction-13-320.jpg)