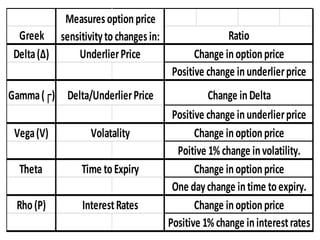
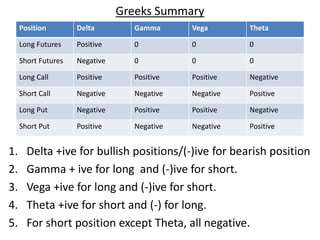
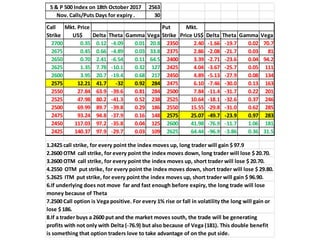
The document discusses the determinants of option price and the Greeks - Delta, Gamma, Vega, Theta, and Rho. It explains that these Greeks measure how sensitive an option's price is to changes in the underlying asset's price, volatility, time to expiration, and interest rates. Specifically, Delta measures change in option price for a $1 change in the underlying, Gamma measures rate of change of Delta, Vega measures change for a 1% volatility change, Theta measures daily time decay, and Rho measures change for a 1% interest rate change. Understanding how the Greeks change is important for risk management and making informed options trading decisions.

1. Determinants of Option Price/Premium
To understand what the Greeks are all about , first
recall the 5 inputs to an option pricing formula:
1. Spot/Market Price. (S)
2. Strike Price. (K)
3. Time to expiry. (T)
4. Volatility (Standard Deviation σ)
5. Risk free Interest rate ( r )
• Except strike price, the other four keep changing
over the life of the option.
• The option price is sensitive to changes in each of
theses 4 factors.

2. The Greeks.
• There are 5 Greeks:
1. Delta
2. Gamma
3. Vega
4. Theta
5. Rho
What do they measure?

3. Greek
Delta(∆)
Gamma(┌)
Vega(V)
Theta
Rho(P)
Positive change inunderlierprice
Change inDelta
Positive change inunderlierprice
Change inoptionprice
Ratio
Positive 1%change ininterestrates
Change inoptionprice
One daychange intime toexpiry.
Change inoptionprice
Poitive 1%change involatility.
Change inoptionprice
Measuresoptionprice
sensitivitytochangesin:
InterestRates
Time toExpiry
Volatality
Delta/UnderlierPrice
UnderlierPrice

4. Why Greeks?
• A risk manager cannot make a well informed
decision to use options, without knowing how
option values change as the factors that
influence option values change.
• Greeks are dynamic, not static.
• As the underlying changes, the Greeks change,
sometimes very rapidly, if the option is close to
expiry.
• Understanding how the Greeks change is critical

5. Delta (D)-1
• Measures the sensitivity of the option to the
movement of the underlying.
• Specifically it indicates how much the premium will
change if the underlying asset changes by 1 point.
(Rs. 1./ US$ 1).
• Deep ITM calls have D approaching 1. Max (S-K,0),
when S > K.
• Far OTM calls have D approaching 0. Max(S-K,0),
when S < K.
• Long Call have positive D between 0 and 1.(+CR).
• Short calls have negative D between 0 and (-) 1.(-
CR)

6. Delta (D). contd.-2
• An ATM/NTM option will have D close to 0.5.
• Delta essentially measures the probability of the
option being in the money at expiry.
• So ATM/NTM having D = 0.5 is logical.
• Deep ITM puts have D approaching (-)1.
Max (K-S,0), when K > S
• Far OTM puts have D approaching 0. Max(K-S,0),
when K < S.
• Long puts have negative D from 0 to -1.(-CR).
• Short put have positive D from 0 to 1.(+CR).
• Many times D is expressed as a number between
0 and 100, rather than 0 to 1

7. Delta
(-)COREL PUTBUYER(K-S) CALLBUYER(S-K) +COREL
DeepITM ATM FarOTM FarOTM ATM DeepITM
(-)1 -0.5 0 0 0.5 +1
1.Deltaforoptionsellers,CallorPut,isofsamemagnitude,butwithoppositesign
2.Ifyourdeltaispositiveyouwanttheunderlyingassetpricetorise.Ifyourdeltais
negativeyouwantittofall.

8. Delta (D). contd.-3
CALL PUT
LONG + (0 to 1) (-) (0 to -1)
SHORT (-) (0 to -1 + (0 to 1)
• Knowledge of delta is vital for option traders because
it is heavily used in margining and risk management

9. Gamma
• Gamma measures change in Delta, with respect
to change in price of underlying.
• Also called 2nd derivative of option premium with
respect to the price of the underlying.
• It works as the acceleration of the delta, the
speed at which an option would go either ITM or
OTM
• High Gamma works against the option seller and
in favour of the option buyer.

10. Vega (V)
• V is a measures change in option premium for a
1% change in the underlying assets volatility.
• It has maximum impact on option value.
• Long positions whether call or puts always have
positive Vega. When volatility rises, long
positions benefit from it.
• Short positions always have negative Vega. Rising
volatility hurts them.
• Vega is highest for ATM options and lowest for
far OTM options

11. Theta (T)-1
• Time value is also called Extrinsic Value. (EV)
• T indicates how much the option price will
theoretically change due to passage of time.
• It is a measure of how much the EV will decay each
day as the option approaches expiry.
• EV goes to 0 as option approaches expiry.
• T is negative for option buyers (Call or Put) and
positive for option sellers(Call or Put).
• For option buyers, the premium will reduce every day
by the approximate amount of T. Favours seller.
• T is option seller’s friend and option buyer’s enemy.
So high theta options are attractive to seller and low
theta to buyers.

12. Theta (T). Contd.-2
• T is highest for ATM options.
• Deep ITM and Far OTM options have T closer to 0.
• Non–directional option strategies rely on income
generation using Theta decay.
• T decays rapidly in the last 30 days to expiry. Specially
true for ATM options.
• Important to understand time value of options for
directional as well as non-directional traders.If underlying
does not move far and fast enough before expiry, the
long trade will lose money because of Theta.
• Sometimes traders buy OTM options because they are
cheap compared to ITM options, forgetting that
probability of OTM options making money is far less than
ITM option.

13. Greeks Summary
Position Delta Gamma Vega Theta
Long Futures Positive 0 0 0
Short Futures Negative 0 0 0
Long Call Positive Positive Positive Negative
Short Call Negative Negative Negative Positive
Long Put Negative Positive Positive Negative
Short Put Positive Negative Negative Positive
1. Delta +ive for bullish positions/(-)ive for bearish position
2. Gamma + ive for long and (-)ive for short.
3. Vega +ive for long and (-)ive for short.
4. Theta +ive for short and (-) for long.
5. For short position except Theta, all negative.

14. Some important observations- options vis-à-vis underlying
• Long option positions are less risky than long
underlying positions.
• 1 to 1 change in option price with underlying
happens only for deep ITM options. Delta 1 for
call and (-1) for put.
• Otherwise option prices move at a pace slower
than underlying price.
• Therefore short positions in deep ITM positions
are as risky as short underlying positions.
• Short positions in ATM and OTM positions are less
risky than short underlying positions.

15. 2563
30
Delta Theta Gamma Vega Delta Theta Gamma Vega
2700 0.35 0.12 -4.09 0.01 20.8 2350 2.40 -1.66 -19.7 0.02 70.7
2675 0.45 0.66 -4.89 0.03 33.8 2375 2.86 -2.08 -21.7 0.03 81
2650 0.70 2.41 -6.54 0.11 64.5 2400 3.39 -2.71 -23.6 0.04 94.2
2625 1.35 7.78 -10.1 0.32 127 2425 4.04 -3.67 -25.7 0.05 111
2600 3.95 20.7 -19.4 0.68 217 2450 4.89 -5.13 -27.9 0.08 134
2575 12.21 41.7 -32 0.92 284 2475 6.10 -7.46 -30.0 0.13 163
2550 27.84 63.9 -39.6 0.81 284 2500 7.84 -11.4 -31.7 0.22 201
2525 47.98 80.2 -41.3 0.52 238 2525 10.64 -18.1 -32.6 0.37 246
2500 69.99 89.7 -39.8 0.29 186 2550 15.55 -29.8 -31.0 0.62 285
2475 93.24 94.8 -37.9 0.16 148 2575 25.07 -49.7 -23.9 0.97 283
2450 117.03 97.2 -35.8 0.04 125 2600 41.98 -76.9 -11.7 1.06 181
2425 140.37 97.9 -29.7 0.03 109 2625 64.44 -96.9 -3.86 0.36 31.5
1.2425 call strike, for every point the index moves up, long trader will gain $ 97.9
2.2600 OTM call strike, for every point the index moves down, long trader will lose $ 20.70.
3.2600 OTM call strike, for every point the index moves up, short trader will lose $ 20.70.
4.2550 OTM put strike, for every point the index moves down, short trader will lose $ 29.80.
5.2625 ITM put strike, for every point the index moves up, short trader will gain $ 96.90.
6.If underlying does not move far and fast enough before expiry, the long trade will lose
money because of Theta
7.2500 Call option is Vega positive. For every 1% rise or fall in volatility the long will gain or
lose $ 186.
8.If a trader buys a 2600 put and the market moves south, the trade will be generating
profits with not only with Delta (-76.9) but also because of Vega (181). This double benefit
is something that option traders love to take advantage of on the put side.
Mkt. Price
US$
Mkt.
Price US$
Call
Strike
Put
Strike
S & P 500 Index on 18th October 2017
Nov. Calls/Puts Days for expiry .