Mayank Bhatia, profile picture
Uploaded byMayank Bhatia
PPS, PPTX81,063 views

Options Trading Strategies

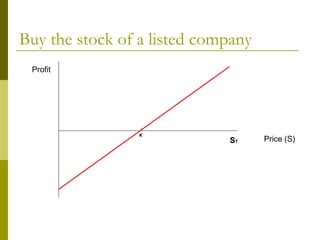
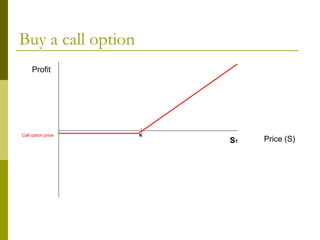
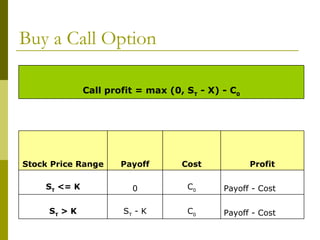
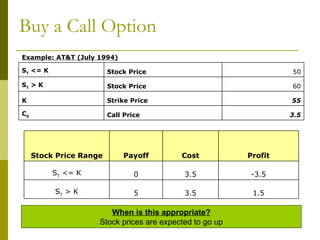
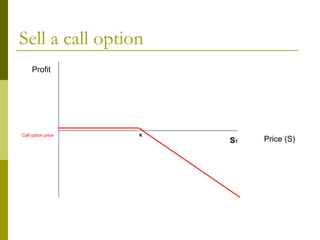
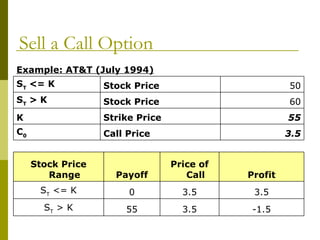
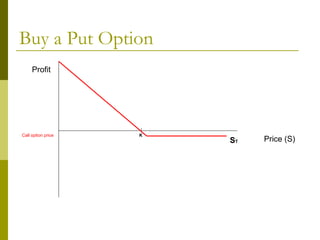
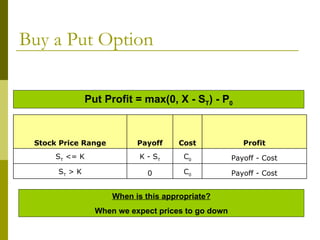
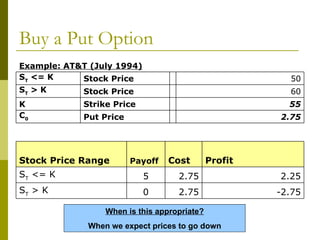
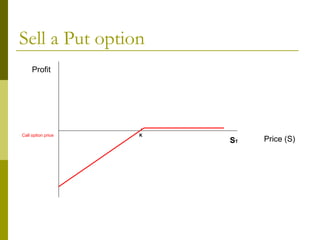
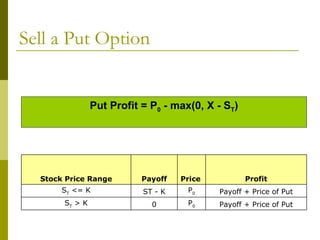
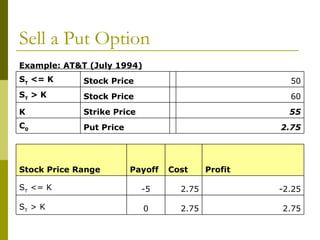
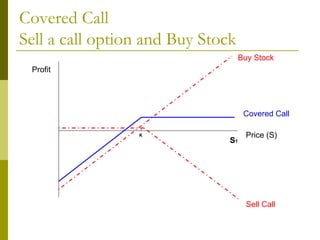
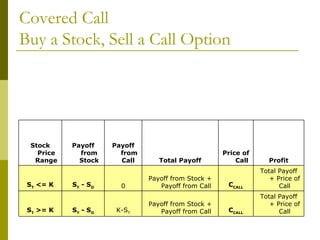
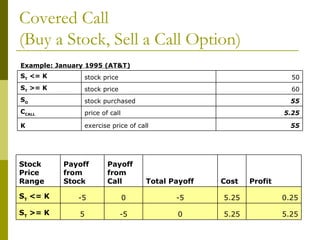
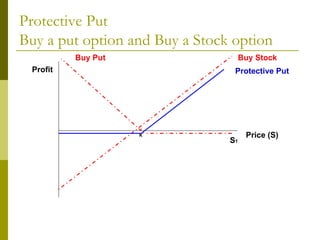
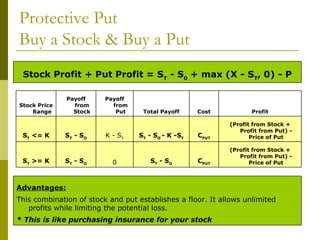
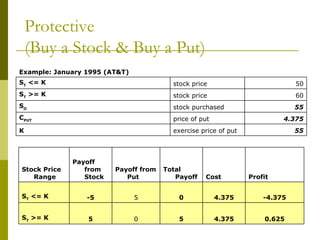
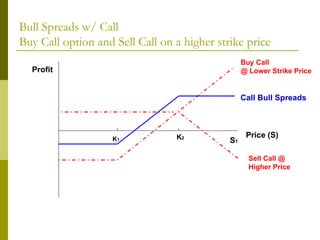
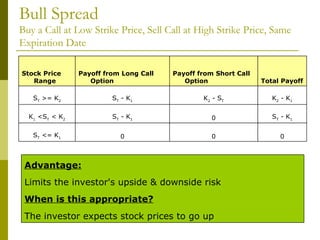
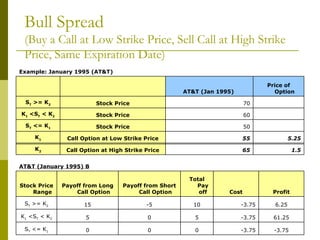
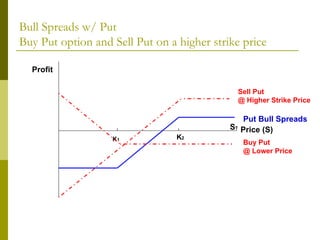
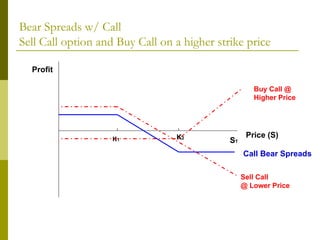
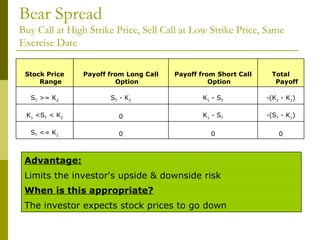
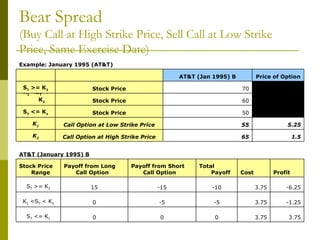
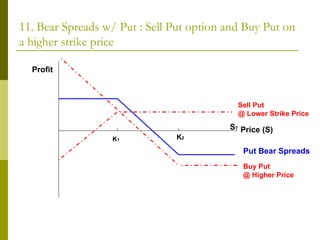
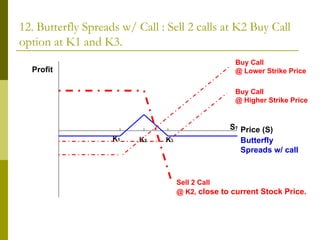
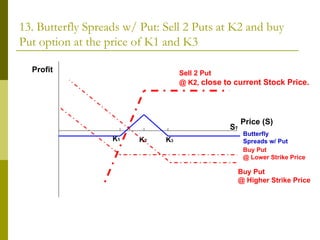
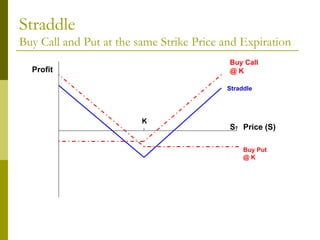
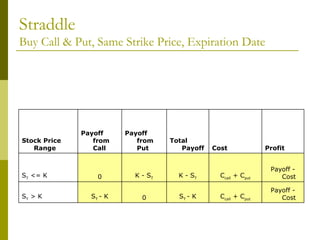
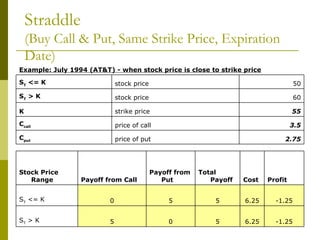
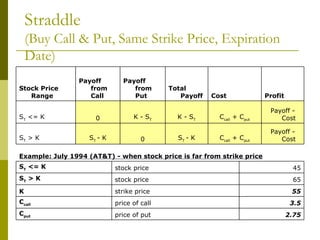
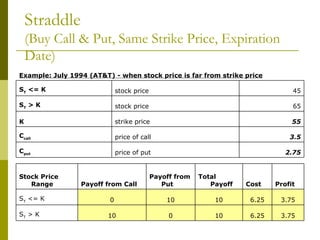
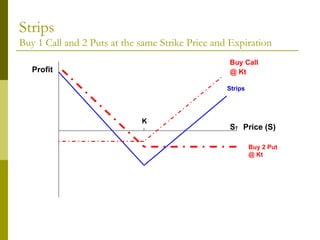
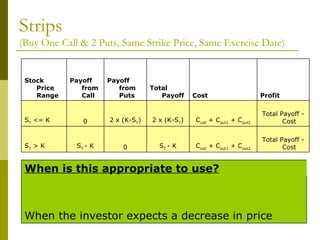
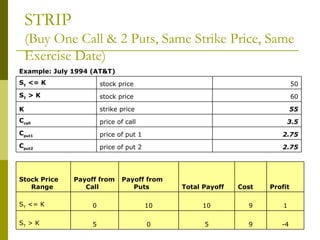
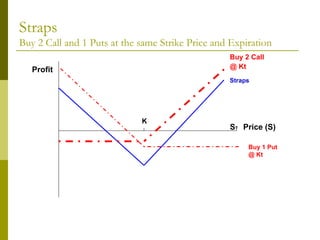
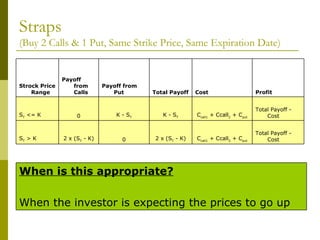
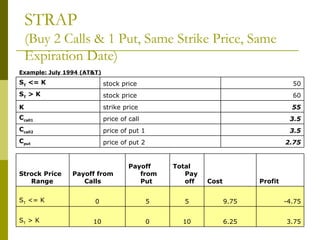
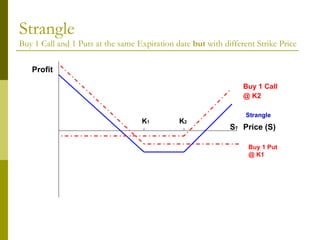
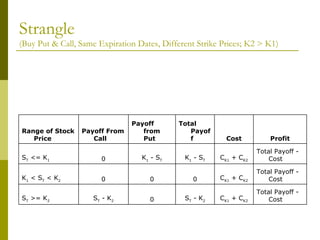
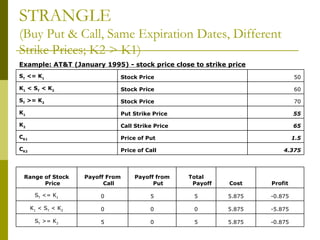
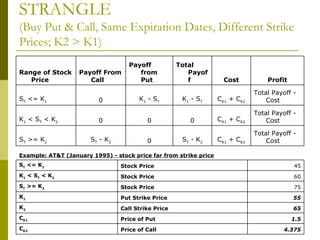
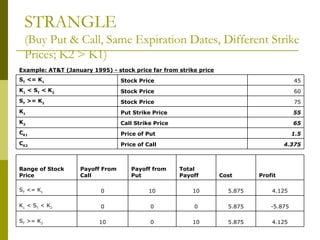
The document covers various options investment strategies, detailing the fundamental concepts of call and put options, as well as various trading strategies, including spreads, straddles, and protective puts. It explains how these strategies can be used based on the investor's expectations of stock price movements, outlining potential profits and risks associated with each. Additionally, it provides practical examples to illustrate the application of these strategies in real-world scenarios.

Embed presentation

Download as PPS, PPTX
The Option Investment Strategies Mayank Bhatia Sandri Supardi Gail Yambao
Options Options: contract giving the buyer right, but not obligation to buy or sell the underlying asset at a certain price on/before the certain date. Two types of Options: Call Option: Gives the holder right to buy an assets at certain price within the specific period of time. Put Option: Gives the holder right to sell an assets at certain price within the specific period of time.
Options Trading Strategies Single Option & a Stock Covered Call Protective Put Spreads Bull Spread Bear Spread Butterfly Spread Calendar Spread Combinations Strip Strap Straddle Strangle
Buy the stock of a listed company Profit Price (S) K S T
Buy a call option Profit Price (S) K S T Call option price
Buy a Call Option Payoff - Cost C 0 S T - K S T > K Payoff - Cost C 0 0 S T <= K Profit Cost Payoff Stock Price Range Call profit = max (0, S T - X) - C 0
Buy a Call Option When is this appropriate? Stock prices are expected to go up 1.5 3.5 5 S T > K -3.5 3.5 0 S T <= K Profit Cost Payoff Stock Price Range 3.5 Call Price C 0 55 Strike Price K 60 Stock Price S T > K 50 Stock Price S T <= K Example: AT&T (July 1994)
Sell a call option Profit Price (S) K S T Call option price
Sell a Call Option Call writer's profit = C 0 - max (0, S T - X) Payoff + Cost C 0 K - S T S T > K Payoff + Cost C 0 0 S T <= K Profit Price of Call Payoff Stock Price Range
Sell a Call Option 3.5 Call Price C 0 55 Strike Price K 60 Stock Price S T > K 50 Stock Price S T <= K Example: AT&T (July 1994) -1.5 3.5 55 S T > K 3.5 3.5 0 S T <= K Profit Price of Call Payoff Stock Price Range
Buy a Put Option Profit Price (S) K S T Call option price
Buy a Put Option Put Profit = max(0, X - S T ) - P 0 When is this appropriate? When we expect prices to go down Payoff - Cost C 0 0 S T > K Payoff - Cost C 0 K - S T S T <= K Profit Cost Payoff Stock Price Range
Buy a Put Option When is this appropriate? When we expect prices to go down 2.75   Put Price C 0 55   Strike Price K 60   Stock Price S T > K 50   Stock Price S T <= K Example: AT&T (July 1994) -2.75 2.75 0 S T > K 2.25 2.75 5 S T <= K Profit Cost Payoff Stock Price Range
Sell a Put option Profit Price (S) K S T Call option price
Sell a Put Option Put Profit = P 0 - max(0, X - S T ) Payoff + Price of Put P 0 0 S T > K Payoff + Price of Put P 0 ST - K S T <= K Profit Price Payoff Stock Price Range
Sell a Put Option 2.75   Put Price C 0 55   Strike Price K 60   Stock Price S T > K 50   Stock Price S T <= K Example: AT&T (July 1994) 2.75 2.75 0 S T > K -2.25 2.75 -5 S T <= K Profit Cost Payoff Stock Price Range
Covered Call Sell a call option and Buy Stock Profit Price (S) K S T Sell Call Covered Call Buy Stock
Covered Call Buy a Stock, Sell a Call Option Total Payoff + Price of Call C CALL Payoff from Stock + Payoff from Call K-S T S T - S O S T >= K Total Payoff + Price of Call C CALL Payoff from Stock + Payoff from Call 0 S T - S O S T <= K Profit Price of Call Total Payoff Payoff from Call Payoff from Stock Stock Price Range
Covered Call (Buy a Stock, Sell a Call Option) 55 exercise price of call K 5.25 price of call C CALL 55 stock purchased S O 60 stock price S T >= K 50 stock price S T <= K Example: January 1995 (AT&T) 5.25 5.25 0 -5 5 S T >= K 0.25 5.25 -5 0 -5 S T <= K Profit Cost Total Payoff Payoff from Call Payoff from Stock Stock Price Range
Covered Call Buy a Stock, Sell a Call Option Advantage: When there is a sharp rise in the stock price, purchased stock protects the seller of the call from pay-off When is this appropriate? A sharp rise in stock prices is expected
Covered Call Buy a Stock, Sell a Call Option Advantage: When there is a sharp rise in the stock price, long stock position &quot;covers&quot; or protects the investor from the payoff on the short call When is this appropriate? A sharp rise in stock prices is expected
Protective Put Buy a put option and Buy a Stock option Profit Price (S) K S T Buy Put Protective Put Buy Stock
Protective Put Buy a Stock & Buy a Put Stock Profit + Put Profit = S T - S 0 + max (X - S T , 0) - P (Profit from Stock + Profit from Put) - Price of Put C PUT S T - S O 0 S T - S O S T >= K (Profit from Stock + Profit from Put) - Price of Put C PUT S T - S O - K -S T K - S T S T - S O S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Stock Stock Price Range * This is like purchasing insurance for your stock This combination of stock and put establishes a floor. It allows unlimited profits while limiting the potential loss. Advantages:
Protective (Buy a Stock & Buy a Put) 55 exercise price of put K 4.375 price of put C PUT 55 stock purchased S O 60 stock price S T >= K 50 stock price S T <= K Example: January 1995 (AT&T) 0.625 4.375 5 0 5 S T >= K -4.375 4.375 0 5 -5 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Stock Stock Price Range
Protective Put Buy a Stock & Buy a Put * This is like purchasing insurance for your stock This combination of stock and put establishes a floor. It allows unlimited profits while limiting the potential loss. Advantages:
Protective (Buy a Stock & Buy a Put) * This is like purchasing insurance for your stock   Should the stock price increase above the strike price, the option would not be exercised & the investor could sell the stock at the higher price & recognize a profit if the stock price is above the overall cost of the position   Should the stock price decline below the strike price before expiration of the option, the investor would exercise the put option & sell his or her stock at the strike price   Potential gains or losses are created from the net effect of a long position in both the put and the stock. This establishes a floor, allowing unlimited profits while limiting the potential loss. Advantages:
Bull Spreads w/ Call Buy Call option and Sell Call on a higher strike price Profit Price (S) K 1 S T Sell Call @ Higher Price Call Bull Spreads Buy Call @ Lower Strike Price K 2
Bull Spread Buy a Call at Low Strike Price, Sell Call at High Strike Price, Same Expiration Date 0 0 0 S T <= K 1 S T - K 1 0 S T - K 1 K 1 <S T < K 2 K 2 - K 1 K 2 - S T S T - K 1 S T >= K 2 Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range The investor expects stock prices to go up When is this appropriate? Limits the investor's upside & downside risk Advantage:
Bull Spread (Buy a Call at Low Strike Price, Sell Call at High Strike Price, Same Expiration Date) 1.5 65 Call Option at High Strike Price K 2 5.25 55 Call Option at Low Strike Price K 1   50 Stock Price S T <= K 1   60 Stock Price K 1 <S T < K 2   70 Stock Price S T >= K 2 Price of Option AT&T (Jan 1995)     Example: January 1995 (AT&T) -3.75 -3.75 0 0 0 S T <= K 1 61.25 -3.75 5 0 5 K 1 <S T < K 2 6.25 -3.75 10 -5 15 S T >= K 2 Profit Cost Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range AT&T (January 1995) B
Bull Spread Buy a Call at Low Strike Price, Sell Call at High Strike Price, Same Expiration Date The investor expects stock prices to go up When is this appropriate? Limits the investor's upside & downside risk Advantage:
Bull Spreads w/ Put Buy Put option and Sell Put on a higher strike price Profit Price (S) K 1 S T Buy Put @ Lower Price Put Bull Spreads Sell Put @ Higher Strike Price K 2
Bear Spreads w/ Call Sell Call option and Buy Call on a higher strike price Profit Price (S) K 1 S T Buy Call @ Higher Price Call Bear Spreads Sell Call @ Lower Price K 2
Bear Spread Buy Call at High Strike Price, Sell Call at Low Strike Price, Same Exercise Date 0 0 0 S T <= K 1 -(S T - K 1 ) K 1 - S T 0 K 1 <S T < K 2 -(K 2 - K 1 ) K 1 - S T S T - K 2 S T >= K 2 Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range The investor expects stock prices to go down When is this appropriate? Limits the investor's upside & downside risk Advantage:
Bear Spread (Buy Call at High Strike Price, Sell Call at Low Strike Price, Same Exercise Date) 1.5 65 Call Option at High Strike Price K 2 5.25 55 Call Option at Low Strike Price K 1   50 Stock Price S T <= K 1   60 Stock Price K 1 <S T < K 2   70 Stock Price S T >= K 2 Price of Option AT&T (Jan 1995) B     Example: January 1995 (AT&T) 3.75 3.75 0 0 0 S T <= K 1 -1.25 3.75 -5 -5 0 K 1 <S T < K 2 -6.25 3.75 -10 -15 15 S T >= K 2 Profit Cost Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range AT&T (January 1995) B
Bear Spread Buy Call at High Strike Price, Sell Call at Low Strike Price, Same Exercise Date The investor expects stock prices to go down When is this appropriate? Limits the investor's upside & downside risk Advantage:
11. Bear Spreads w/ Put : Sell Put option and Buy Put on a higher strike price Profit Price (S) K 1 S T Buy Put @ Higher Price Put Bear Spreads Sell Put @ Lower Strike Price K 2
12. Butterfly Spreads w/ Call : Sell 2 calls at K2 Buy Call option at K1 and K3. Profit Price (S) K 1 S T Sell 2 Call @ K2, close to current Stock Price. Butterfly Spreads w/ call Buy Call @ Higher Strike Price K 3 K 2 Buy Call @ Lower Strike Price
13. Butterfly Spreads w/ Put: Sell 2 Puts at K2 and buy Put option at the price of K1 and K3 Profit Price (S) K 1 S T Sell 2 Put @ K2, close to current Stock Price. Butterfly Spreads w/ Put Buy Put @ Lower Strike Price K 3 K 2 Buy Put @ Higher Strike Price
Straddle Buy Call and Put at the same Strike Price and Expiration Profit Price (S) S T Buy Call @ K Straddle Buy Put @ K K
Straddle Buy Call & Put, Same Strike Price, Expiration Date Payoff - Cost C call + C put S T - K 0 S T - K S T > K Payoff - Cost C call + C put K - S T K - S T 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range
Straddle (Buy Call & Put, Same Strike Price, Expiration Date) 2.75 price of put C put 3.5 price of call C call 55 strike price K 60 stock price S T > K 50 stock price S T <= K Example: July 1994 (AT&T) - when stock price is close to strike price -1.25 6.25 5 0 5 S T > K -1.25 6.25 5 5 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range
Straddle (Buy Call & Put, Same Strike Price, Expiration Date) Payoff - Cost C call + C put S T - K 0 S T - K S T > K Payoff - Cost C call + C put K - S T K - S T 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range 2.75 price of put C put 3.5 price of call C call 55 strike price K 65 stock price S T > K 45 stock price S T <= K Example: July 1994 (AT&T) - when stock price is far from strike price
Straddle (Buy Call & Put, Same Strike Price, Expiration Date) 2.75 price of put C put 3.5 price of call C call 55 strike price K 65 stock price S T > K 45 stock price S T <= K Example: July 1994 (AT&T) - when stock price is far from strike price 3.75 6.25 10 0 10 S T > K 3.75 6.25 10 10 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range
Straddle Buy Call & Put, Same Strike Price, Expiration Date Investor is expecting a large move in a stock price but does not know in which direction the move will be; a big jump in the price of a company’s stock is expected; a takeover bid for the company or outcome of a major lawsuit is expected to be announced soon When is this appropriate to use? If stock price is close to strike price at expiration of options --> LOSS Disadvantage If there is a sufficiently large move in either direction, a significant PROFIT will result Advantage
Strips Buy 1 Call and 2 Puts at the same Strike Price and Expiration Profit Price (S) S T Buy Call @ Kt Strips Buy 2 Put @ Kt K
Strips (Buy One Call & 2 Puts, Same Strike Price, Same Exercise Date) Total Payoff - Cost C call + C put1 + C put2 S T - K 0 S T - K S T > K Total Payoff - Cost C call + C put1 + C put2 2 x (K-S T ) 2 x (K-S T ) 0 S T <= K Profit Cost Total Payoff Payoff from Puts Payoff from Call Stock Price Range When the investor expects a decrease in price When is this appropriate to use?
STRIP (Buy One Call & 2 Puts, Same Strike Price, Same Exercise Date) 2.75 price of put 2 C put2 2.75 price of put 1 C put1 3.5 price of call C call 55 strike price K 60 stock price S T > K 50 stock price S T <= K Example: July 1994 (AT&T) -4 9 5 0 5 S T > K 1 9 10 10 0 S T <= K Profit Cost Total Payoff Payoff from Puts Payoff from Call Stock Price Range
Strips Buy One Call & 2 Puts, Same Strike Price, Same Exercise Date When the investor is expecting the prices to decrease When is this appropriate to use?
Straps Buy 2 Call and 1 Puts at the same Strike Price and Expiration Profit Price (S) S T Buy 2 Call @ Kt Straps Buy 1 Put @ Kt K
Straps (Buy 2 Calls & 1 Put, Same Strike Price, Same Expiration Date) Total Payoff - Cost C call1 + Ccall 2 + C put 2 x (S T - K) 0 2 x (S T - K) S T > K Total Payoff - Cost C call1 + Ccall 2 + C put K - S T K - S T 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Calls Strock Price Range When the investor is expecting the prices to go up When is this appropriate?
STRAP (Buy 2 Calls & 1 Put, Same Strike Price, Same Expiration Date) 2.75 price of put 2 C put 3.5 price of put 1 C call2 3.5 price of call C call1 55 strike price K 60 stock price S T > K 50 stock price S T <= K Example: July 1994 (AT&T) 3.75 6.25 10 0 10 S T > K -4.75 9.75 5 5 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Calls Strock Price Range
Straps (Buy 2 Calls & 1 Put, Same Strike Price, Same Expiration Date) The investor is betting that there will be a big stock price move; however, an increase in the stock price is considered to be more likely than a decrease When is this appropriate?
Strangle Buy 1 Call and 1 Puts at the same Expiration date but with different Strike Price Profit Price (S) S T Buy 1 Call @ K2 Strangle Buy 1 Put @ K1 K 1 K 2
Strangle (Buy Put & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) Total Payoff - Cost C K1 + C K2 S T - K 2 0 S T - K 2 S T >= K 2 Total Payoff - Cost C K1 + C K2 0 0 0 K 1 < S T < K 2 Total Payoff - Cost C K1 + C K2 K 1 - S T K 1 - S T 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price
STRANGLE (Buy Put & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) 4.375 Price of Call C K2 1.5 Price of Put C K1 65 Call Strike Price K 2 55 Put Strike Price K 1 70 Stock Price S T >= K 2 60 Stock Price K 1 < S T < K 2 50 Stock Price S T <= K 1 Example: AT&T (January 1995) - stock price close to strike price -0.875 5.875 5 0 5 S T >= K 2 -5.875 5.875 0 0 0 K 1 < S T < K 2 -0.875 5.875 5 5 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price
STRANGLE (Buy Put & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) Total Payoff - Cost C K1 + C K2 S T - K 2 0 S T - K 2 S T >= K 2 Total Payoff - Cost C K1 + C K2 0 0 0 K 1 < S T < K 2 Total Payoff - Cost C K1 + C K2 K 1 - S T K 1 - S T 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price 4.375 Price of Call C K2 1.5 Price of Put C K1 65 Call Strike Price K 2 55 Put Strike Price K 1 75 Stock Price S T >= K 2 60 Stock Price K 1 < S T < K 2 45 Stock Price S T <= K 1 Example: AT&T (January 1995) - stock price far from strike price
STRANGLE (Buy Put & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) 4.375 Price of Call C K2 1.5 Price of Put C K1 65 Call Strike Price K 2 55 Put Strike Price K 1 75 Stock Price S T >= K 2 60 Stock Price K 1 < S T < K 2 45 Stock Price S T <= K 1 Example: AT&T (January 1995) - stock price far from strike price 4.125 5.875 10 0 10 S T >= K 2 -5.875 5.875 0 0 0 K 1 < S T < K 2 4.125 5.875 10 10 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price
Strangle (Buy Put & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) The farther strike prices are apart, the less the downside risk and the farther the stock price has to move for a profit to be realized Advantage   The downside risk if the stock price ends up at a central value is less with a strangle Disadvantage   The stock price has to move farther in a strangle than in a straddle for the investor to make a profit The investor is betting that there will be a large price move, but is uncertain whether it will be an increase or decrease. When is this appropriate?

More Related Content

PPTX
Option Strategies
byAshwini Mahale
 
PPT
Options
byashwin_sharma
 
PPTX
Fundamentals of Option Contracts
byFortuna Favi et Fortus Ltd.
 
PPTX
Options trading strategies
byankursaraf92
 
PPT
Options
bymuratcoskun
 
PPTX
Options strategies
byPavan Makhija
 
PPTX
Derivatives- CALL AND PUT OPTIONS
byDinesh Kumar
 
PPTX
Derivatives: Options and it's Greeks
byDinesh Kumar
 
Option Strategies
byAshwini Mahale
 
Options
byashwin_sharma
 
Fundamentals of Option Contracts
byFortuna Favi et Fortus Ltd.
 
Options trading strategies
byankursaraf92
 
Options
bymuratcoskun
 
Options strategies
byPavan Makhija
 
Derivatives- CALL AND PUT OPTIONS
byDinesh Kumar
 
Derivatives: Options and it's Greeks
byDinesh Kumar
 

What's hot

PDF
Option trading strategies
bysivaram12321
 
PPTX
Basics of options
byRohit Bombale
 
PPTX
Straddles and strangles
byTaruMaheshwari3
 
PPTX
Options trading presentation
byBrian Hyde
 
PPT
Options Trading Strategies
byluv_sharma
 
PPTX
Option ( Derivatives)
byMuhammed Nowfal S
 
PDF
Lecture no 6 covered call
byProfessional Training Academy
 
PPTX
Payoff options
byAnushya D
 
PPT
Technical Analysis Of Stock Market
bym.jalan
 
PPT
Bacics Of Derivatives
byyehyakhan
 
PPTX
Support resistance trading strategies
byHimanshu Patil
 
PPTX
Dow theory by P. Sai Prathyusha (1ST M.COM BUSINESS FINANCE)
bySaiLakshmi115
 
PPTX
option basics
byRudreshSamant
 
PPTX
put call parity
byKrystal Skull
 
PPTX
Option strategies
byNilay Mishra
 
PPTX
Option strategies
byRaghav Sharma
 
PPTX
Financial derivatives
bymittali1503
 
PDF
Moving average -Technical Analysis
byDr.Subhransu Sekhar Jena
 
PPT
Futures and options
byAltacit Global
 
PPTX
Relative Strength Index
byRajaKrishnan M
 
Option trading strategies
bysivaram12321
 
Basics of options
byRohit Bombale
 
Straddles and strangles
byTaruMaheshwari3
 
Options trading presentation
byBrian Hyde
 
Options Trading Strategies
byluv_sharma
 
Option ( Derivatives)
byMuhammed Nowfal S
 
Lecture no 6 covered call
byProfessional Training Academy
 
Payoff options
byAnushya D
 
Technical Analysis Of Stock Market
bym.jalan
 
Bacics Of Derivatives
byyehyakhan
 
Support resistance trading strategies
byHimanshu Patil
 
Dow theory by P. Sai Prathyusha (1ST M.COM BUSINESS FINANCE)
bySaiLakshmi115
 
option basics
byRudreshSamant
 
put call parity
byKrystal Skull
 
Option strategies
byNilay Mishra
 
Option strategies
byRaghav Sharma
 
Financial derivatives
bymittali1503
 
Moving average -Technical Analysis
byDr.Subhransu Sekhar Jena
 
Futures and options
byAltacit Global
 
Relative Strength Index
byRajaKrishnan M
 

Viewers also liked

PPTX
Formation of insurance contract
bySalma Amr El-Azhary
 
PPTX
ORGANIZATIONAL CITIZENSHIP BEHAVIOR
byCihan Baksi, MBA
 
PPT
Insurance
byvishakeb
 
PPTX
Organizational citizenship behavior
byIxhar Khan
 
PPTX
Ocb group 2
byChetan Chawhan
 
PPTX
Organizational citizenship behavior (ocb)
byzachmeier
 
PPT
Chapter 2:Insurance Contract
byMarya Sholevar
 
PPT
Organizational Citizenship Behavior
bySharath g
 
PPTX
Insurance contract
byNagindas Khandwala College
 
PPSX
2. Insurance - Classification of Insurance
byKoffee Financial
 
PPTX
Corporate risk management
byPraxiom
 
PDF
Corporate Risk Management
byShravan Bhumkar
 
PPT
Gallup Q12's Employee Engagement Findings
byPaul Sohn
 
PPTX
Employee Engagement
byNational HRD Network
 
PPTX
Principles of insurance
byIndrajeet Kamble
 
PPTX
Life insurance ppt
byjaypujara007
 
Formation of insurance contract
bySalma Amr El-Azhary
 
ORGANIZATIONAL CITIZENSHIP BEHAVIOR
byCihan Baksi, MBA
 
Insurance
byvishakeb
 
Organizational citizenship behavior
byIxhar Khan
 
Ocb group 2
byChetan Chawhan
 
Organizational citizenship behavior (ocb)
byzachmeier
 
Chapter 2:Insurance Contract
byMarya Sholevar
 
Organizational Citizenship Behavior
bySharath g
 
Insurance contract
byNagindas Khandwala College
 
2. Insurance - Classification of Insurance
byKoffee Financial
 
Corporate risk management
byPraxiom
 
Corporate Risk Management
byShravan Bhumkar
 
Gallup Q12's Employee Engagement Findings
byPaul Sohn
 
Employee Engagement
byNational HRD Network
 
Principles of insurance
byIndrajeet Kamble
 
Life insurance ppt
byjaypujara007
 

Similar to Options Trading Strategies

PPT
Options Trading
byAlfred Rodrigues
 
PPT
Options Presentation Introduction to Corporate Finance
bymuratcoskun
 
PPTX
Option-strategies of derivative products
byJyotiSinghal25
 
PDF
The Options JumpStarter - A Beginner's Guide To Profitable Options Trading | ...
byClayRoyer1
 
PPTX
Derivatives in India
bySrinivas Mittapelli
 
PPT
F B E559f15 Trading Strategies
byuichong
 
PPT
Saim ppt
byamitnanglu
 
PPTX
Money Spreads
byvissie101
 
PPTX
FPA Conference Presentation in Anaheim, Ca 10-11-2009
byseaneheron
 
PPT
About Options
byRoy Alford
 
PPT
Fully explained Options_trading_strategies.ppt
byKharvoPati
 
PPT
Trade12
byTrade12
 
PPT
How to Protect and Enhance Your Investment Portfolio
byboblawson
 
PPT
Stock Options 101 Jul28 10
bydavidsaxe
 
PPTX
Call option and buy option of sharemarket.pptx
byNitPatil1
 
PPTX
Financial markets and Institution options.pptx
bysiyad22
 
PPT
Session_Option Strategy.ppt
byMDKHALID57
 
PPT
Derivative - Options
byThe Stockker
 
PDF
Options For Traders
bypateltarunmba
 
PPTX
Option Combinations and spreads for understanding the concept well
bysharmarohit5784
 
Options Trading
byAlfred Rodrigues
 
Options Presentation Introduction to Corporate Finance
bymuratcoskun
 
Option-strategies of derivative products
byJyotiSinghal25
 
The Options JumpStarter - A Beginner's Guide To Profitable Options Trading | ...
byClayRoyer1
 
Derivatives in India
bySrinivas Mittapelli
 
F B E559f15 Trading Strategies
byuichong
 
Saim ppt
byamitnanglu
 
Money Spreads
byvissie101
 
FPA Conference Presentation in Anaheim, Ca 10-11-2009
byseaneheron
 
About Options
byRoy Alford
 
Fully explained Options_trading_strategies.ppt
byKharvoPati
 
Trade12
byTrade12
 
How to Protect and Enhance Your Investment Portfolio
byboblawson
 
Stock Options 101 Jul28 10
bydavidsaxe
 
Call option and buy option of sharemarket.pptx
byNitPatil1
 
Financial markets and Institution options.pptx
bysiyad22
 
Session_Option Strategy.ppt
byMDKHALID57
 
Derivative - Options
byThe Stockker
 
Options For Traders
bypateltarunmba
 
Option Combinations and spreads for understanding the concept well
bysharmarohit5784
 

Options Trading Strategies

  • 1.
    The Option InvestmentStrategies Mayank Bhatia Sandri Supardi Gail Yambao
  • 2.
    Options Options: contract giving the buyer right, but not obligation to buy or sell the underlying asset at a certain price on/before the certain date. Two types of Options: Call Option: Gives the holder right to buy an assets at certain price within the specific period of time. Put Option: Gives the holder right to sell an assets at certain price within the specific period of time.
  • 3.
    Options Trading StrategiesSingle Option & a Stock Covered Call Protective Put Spreads Bull Spread Bear Spread Butterfly Spread Calendar Spread Combinations Strip Strap Straddle Strangle
  • 4.
    Buy the stockof a listed company Profit Price (S) K S T
  • 5.
    Buy a calloption Profit Price (S) K S T Call option price
  • 6.
    Buy a CallOption Payoff - Cost C 0 S T - K S T > K Payoff - Cost C 0 0 S T <= K Profit Cost Payoff Stock Price Range Call profit = max (0, S T - X) - C 0
  • 7.
    Buy a CallOption When is this appropriate? Stock prices are expected to go up 1.5 3.5 5 S T > K -3.5 3.5 0 S T <= K Profit Cost Payoff Stock Price Range 3.5 Call Price C 0 55 Strike Price K 60 Stock Price S T > K 50 Stock Price S T <= K Example: AT&T (July 1994)
  • 8.
    Sell a calloption Profit Price (S) K S T Call option price
  • 9.
    Sell a CallOption Call writer's profit = C 0 - max (0, S T - X) Payoff + Cost C 0 K - S T S T > K Payoff + Cost C 0 0 S T <= K Profit Price of Call Payoff Stock Price Range
  • 10.
    Sell a CallOption 3.5 Call Price C 0 55 Strike Price K 60 Stock Price S T > K 50 Stock Price S T <= K Example: AT&T (July 1994) -1.5 3.5 55 S T > K 3.5 3.5 0 S T <= K Profit Price of Call Payoff Stock Price Range
  • 11.
    Buy a PutOption Profit Price (S) K S T Call option price
  • 12.
    Buy a PutOption Put Profit = max(0, X - S T ) - P 0 When is this appropriate? When we expect prices to go down Payoff - Cost C 0 0 S T > K Payoff - Cost C 0 K - S T S T <= K Profit Cost Payoff Stock Price Range
  • 13.
    Buy a PutOption When is this appropriate? When we expect prices to go down 2.75   Put Price C 0 55   Strike Price K 60   Stock Price S T > K 50   Stock Price S T <= K Example: AT&T (July 1994) -2.75 2.75 0 S T > K 2.25 2.75 5 S T <= K Profit Cost Payoff Stock Price Range
  • 14.
    Sell a Putoption Profit Price (S) K S T Call option price
  • 15.
    Sell a PutOption Put Profit = P 0 - max(0, X - S T ) Payoff + Price of Put P 0 0 S T > K Payoff + Price of Put P 0 ST - K S T <= K Profit Price Payoff Stock Price Range
  • 16.
    Sell a PutOption 2.75   Put Price C 0 55   Strike Price K 60   Stock Price S T > K 50   Stock Price S T <= K Example: AT&T (July 1994) 2.75 2.75 0 S T > K -2.25 2.75 -5 S T <= K Profit Cost Payoff Stock Price Range
  • 17.
    Covered Call Sell a call option and Buy Stock Profit Price (S) K S T Sell Call Covered Call Buy Stock
  • 18.
    Covered Call Buy a Stock, Sell a Call Option Total Payoff + Price of Call C CALL Payoff from Stock + Payoff from Call K-S T S T - S O S T >= K Total Payoff + Price of Call C CALL Payoff from Stock + Payoff from Call 0 S T - S O S T <= K Profit Price of Call Total Payoff Payoff from Call Payoff from Stock Stock Price Range
  • 19.
    Covered Call (Buy a Stock, Sell a Call Option) 55 exercise price of call K 5.25 price of call C CALL 55 stock purchased S O 60 stock price S T >= K 50 stock price S T <= K Example: January 1995 (AT&T) 5.25 5.25 0 -5 5 S T >= K 0.25 5.25 -5 0 -5 S T <= K Profit Cost Total Payoff Payoff from Call Payoff from Stock Stock Price Range
  • 20.
    Covered Call Buy a Stock, Sell a Call Option Advantage: When there is a sharp rise in the stock price, purchased stock protects the seller of the call from pay-off When is this appropriate? A sharp rise in stock prices is expected
  • 21.
    Covered Call Buy a Stock, Sell a Call Option Advantage: When there is a sharp rise in the stock price, long stock position &quot;covers&quot; or protects the investor from the payoff on the short call When is this appropriate? A sharp rise in stock prices is expected
  • 22.
    Protective Put Buya put option and Buy a Stock option Profit Price (S) K S T Buy Put Protective Put Buy Stock
  • 23.
    Protective Put Buy a Stock & Buy a Put Stock Profit + Put Profit = S T - S 0 + max (X - S T , 0) - P (Profit from Stock + Profit from Put) - Price of Put C PUT S T - S O 0 S T - S O S T >= K (Profit from Stock + Profit from Put) - Price of Put C PUT S T - S O - K -S T K - S T S T - S O S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Stock Stock Price Range * This is like purchasing insurance for your stock This combination of stock and put establishes a floor. It allows unlimited profits while limiting the potential loss. Advantages:
  • 24.
    Protective (Buya Stock & Buy a Put) 55 exercise price of put K 4.375 price of put C PUT 55 stock purchased S O 60 stock price S T >= K 50 stock price S T <= K Example: January 1995 (AT&T) 0.625 4.375 5 0 5 S T >= K -4.375 4.375 0 5 -5 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Stock Stock Price Range
  • 25.
    Protective Put Buya Stock & Buy a Put * This is like purchasing insurance for your stock This combination of stock and put establishes a floor. It allows unlimited profits while limiting the potential loss. Advantages:
  • 26.
    Protective (Buya Stock & Buy a Put) * This is like purchasing insurance for your stock   Should the stock price increase above the strike price, the option would not be exercised & the investor could sell the stock at the higher price & recognize a profit if the stock price is above the overall cost of the position   Should the stock price decline below the strike price before expiration of the option, the investor would exercise the put option & sell his or her stock at the strike price   Potential gains or losses are created from the net effect of a long position in both the put and the stock. This establishes a floor, allowing unlimited profits while limiting the potential loss. Advantages:
  • 27.
    Bull Spreads w/Call Buy Call option and Sell Call on a higher strike price Profit Price (S) K 1 S T Sell Call @ Higher Price Call Bull Spreads Buy Call @ Lower Strike Price K 2
  • 28.
    Bull Spread Buya Call at Low Strike Price, Sell Call at High Strike Price, Same Expiration Date 0 0 0 S T <= K 1 S T - K 1 0 S T - K 1 K 1 <S T < K 2 K 2 - K 1 K 2 - S T S T - K 1 S T >= K 2 Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range The investor expects stock prices to go up When is this appropriate? Limits the investor's upside & downside risk Advantage:
  • 29.
    Bull Spread (Buya Call at Low Strike Price, Sell Call at High Strike Price, Same Expiration Date) 1.5 65 Call Option at High Strike Price K 2 5.25 55 Call Option at Low Strike Price K 1   50 Stock Price S T <= K 1   60 Stock Price K 1 <S T < K 2   70 Stock Price S T >= K 2 Price of Option AT&T (Jan 1995)     Example: January 1995 (AT&T) -3.75 -3.75 0 0 0 S T <= K 1 61.25 -3.75 5 0 5 K 1 <S T < K 2 6.25 -3.75 10 -5 15 S T >= K 2 Profit Cost Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range AT&T (January 1995) B
  • 30.
    Bull Spread Buya Call at Low Strike Price, Sell Call at High Strike Price, Same Expiration Date The investor expects stock prices to go up When is this appropriate? Limits the investor's upside & downside risk Advantage:
  • 31.
    Bull Spreads w/Put Buy Put option and Sell Put on a higher strike price Profit Price (S) K 1 S T Buy Put @ Lower Price Put Bull Spreads Sell Put @ Higher Strike Price K 2
  • 32.
    Bear Spreads w/Call Sell Call option and Buy Call on a higher strike price Profit Price (S) K 1 S T Buy Call @ Higher Price Call Bear Spreads Sell Call @ Lower Price K 2
  • 33.
    Bear Spread BuyCall at High Strike Price, Sell Call at Low Strike Price, Same Exercise Date 0 0 0 S T <= K 1 -(S T - K 1 ) K 1 - S T 0 K 1 <S T < K 2 -(K 2 - K 1 ) K 1 - S T S T - K 2 S T >= K 2 Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range The investor expects stock prices to go down When is this appropriate? Limits the investor's upside & downside risk Advantage:
  • 34.
    Bear Spread (BuyCall at High Strike Price, Sell Call at Low Strike Price, Same Exercise Date) 1.5 65 Call Option at High Strike Price K 2 5.25 55 Call Option at Low Strike Price K 1   50 Stock Price S T <= K 1   60 Stock Price K 1 <S T < K 2   70 Stock Price S T >= K 2 Price of Option AT&T (Jan 1995) B     Example: January 1995 (AT&T) 3.75 3.75 0 0 0 S T <= K 1 -1.25 3.75 -5 -5 0 K 1 <S T < K 2 -6.25 3.75 -10 -15 15 S T >= K 2 Profit Cost Total Payoff Payoff from Short Call Option Payoff from Long Call Option Stock Price Range AT&T (January 1995) B
  • 35.
    Bear Spread BuyCall at High Strike Price, Sell Call at Low Strike Price, Same Exercise Date The investor expects stock prices to go down When is this appropriate? Limits the investor's upside & downside risk Advantage:
  • 36.
    11. Bear Spreadsw/ Put : Sell Put option and Buy Put on a higher strike price Profit Price (S) K 1 S T Buy Put @ Higher Price Put Bear Spreads Sell Put @ Lower Strike Price K 2
  • 37.
    12. Butterfly Spreadsw/ Call : Sell 2 calls at K2 Buy Call option at K1 and K3. Profit Price (S) K 1 S T Sell 2 Call @ K2, close to current Stock Price. Butterfly Spreads w/ call Buy Call @ Higher Strike Price K 3 K 2 Buy Call @ Lower Strike Price
  • 38.
    13. Butterfly Spreadsw/ Put: Sell 2 Puts at K2 and buy Put option at the price of K1 and K3 Profit Price (S) K 1 S T Sell 2 Put @ K2, close to current Stock Price. Butterfly Spreads w/ Put Buy Put @ Lower Strike Price K 3 K 2 Buy Put @ Higher Strike Price
  • 39.
    Straddle Buy Calland Put at the same Strike Price and Expiration Profit Price (S) S T Buy Call @ K Straddle Buy Put @ K K
  • 40.
    Straddle Buy Call& Put, Same Strike Price, Expiration Date Payoff - Cost C call + C put S T - K 0 S T - K S T > K Payoff - Cost C call + C put K - S T K - S T 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range
  • 41.
    Straddle (Buy Call& Put, Same Strike Price, Expiration Date) 2.75 price of put C put 3.5 price of call C call 55 strike price K 60 stock price S T > K 50 stock price S T <= K Example: July 1994 (AT&T) - when stock price is close to strike price -1.25 6.25 5 0 5 S T > K -1.25 6.25 5 5 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range
  • 42.
    Straddle (Buy Call& Put, Same Strike Price, Expiration Date) Payoff - Cost C call + C put S T - K 0 S T - K S T > K Payoff - Cost C call + C put K - S T K - S T 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range 2.75 price of put C put 3.5 price of call C call 55 strike price K 65 stock price S T > K 45 stock price S T <= K Example: July 1994 (AT&T) - when stock price is far from strike price
  • 43.
    Straddle (Buy Call& Put, Same Strike Price, Expiration Date) 2.75 price of put C put 3.5 price of call C call 55 strike price K 65 stock price S T > K 45 stock price S T <= K Example: July 1994 (AT&T) - when stock price is far from strike price 3.75 6.25 10 0 10 S T > K 3.75 6.25 10 10 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Call Stock Price Range
  • 44.
    Straddle Buy Call& Put, Same Strike Price, Expiration Date Investor is expecting a large move in a stock price but does not know in which direction the move will be; a big jump in the price of a company’s stock is expected; a takeover bid for the company or outcome of a major lawsuit is expected to be announced soon When is this appropriate to use? If stock price is close to strike price at expiration of options --> LOSS Disadvantage If there is a sufficiently large move in either direction, a significant PROFIT will result Advantage
  • 45.
    Strips Buy 1Call and 2 Puts at the same Strike Price and Expiration Profit Price (S) S T Buy Call @ Kt Strips Buy 2 Put @ Kt K
  • 46.
    Strips (Buy OneCall & 2 Puts, Same Strike Price, Same Exercise Date) Total Payoff - Cost C call + C put1 + C put2 S T - K 0 S T - K S T > K Total Payoff - Cost C call + C put1 + C put2 2 x (K-S T ) 2 x (K-S T ) 0 S T <= K Profit Cost Total Payoff Payoff from Puts Payoff from Call Stock Price Range When the investor expects a decrease in price When is this appropriate to use?
  • 47.
    STRIP (Buy OneCall & 2 Puts, Same Strike Price, Same Exercise Date) 2.75 price of put 2 C put2 2.75 price of put 1 C put1 3.5 price of call C call 55 strike price K 60 stock price S T > K 50 stock price S T <= K Example: July 1994 (AT&T) -4 9 5 0 5 S T > K 1 9 10 10 0 S T <= K Profit Cost Total Payoff Payoff from Puts Payoff from Call Stock Price Range
  • 48.
    Strips Buy OneCall & 2 Puts, Same Strike Price, Same Exercise Date When the investor is expecting the prices to decrease When is this appropriate to use?
  • 49.
    Straps Buy 2 Call and 1 Puts at the same Strike Price and Expiration Profit Price (S) S T Buy 2 Call @ Kt Straps Buy 1 Put @ Kt K
  • 50.
    Straps (Buy 2Calls & 1 Put, Same Strike Price, Same Expiration Date) Total Payoff - Cost C call1 + Ccall 2 + C put 2 x (S T - K) 0 2 x (S T - K) S T > K Total Payoff - Cost C call1 + Ccall 2 + C put K - S T K - S T 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Calls Strock Price Range When the investor is expecting the prices to go up When is this appropriate?
  • 51.
    STRAP (Buy 2Calls & 1 Put, Same Strike Price, Same Expiration Date) 2.75 price of put 2 C put 3.5 price of put 1 C call2 3.5 price of call C call1 55 strike price K 60 stock price S T > K 50 stock price S T <= K Example: July 1994 (AT&T) 3.75 6.25 10 0 10 S T > K -4.75 9.75 5 5 0 S T <= K Profit Cost Total Payoff Payoff from Put Payoff from Calls Strock Price Range
  • 52.
    Straps (Buy 2Calls & 1 Put, Same Strike Price, Same Expiration Date) The investor is betting that there will be a big stock price move; however, an increase in the stock price is considered to be more likely than a decrease When is this appropriate?
  • 53.
    Strangle Buy 1Call and 1 Puts at the same Expiration date but with different Strike Price Profit Price (S) S T Buy 1 Call @ K2 Strangle Buy 1 Put @ K1 K 1 K 2
  • 54.
    Strangle (BuyPut & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) Total Payoff - Cost C K1 + C K2 S T - K 2 0 S T - K 2 S T >= K 2 Total Payoff - Cost C K1 + C K2 0 0 0 K 1 < S T < K 2 Total Payoff - Cost C K1 + C K2 K 1 - S T K 1 - S T 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price
  • 55.
    STRANGLE (BuyPut & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) 4.375 Price of Call C K2 1.5 Price of Put C K1 65 Call Strike Price K 2 55 Put Strike Price K 1 70 Stock Price S T >= K 2 60 Stock Price K 1 < S T < K 2 50 Stock Price S T <= K 1 Example: AT&T (January 1995) - stock price close to strike price -0.875 5.875 5 0 5 S T >= K 2 -5.875 5.875 0 0 0 K 1 < S T < K 2 -0.875 5.875 5 5 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price
  • 56.
    STRANGLE (BuyPut & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) Total Payoff - Cost C K1 + C K2 S T - K 2 0 S T - K 2 S T >= K 2 Total Payoff - Cost C K1 + C K2 0 0 0 K 1 < S T < K 2 Total Payoff - Cost C K1 + C K2 K 1 - S T K 1 - S T 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price 4.375 Price of Call C K2 1.5 Price of Put C K1 65 Call Strike Price K 2 55 Put Strike Price K 1 75 Stock Price S T >= K 2 60 Stock Price K 1 < S T < K 2 45 Stock Price S T <= K 1 Example: AT&T (January 1995) - stock price far from strike price
  • 57.
    STRANGLE (BuyPut & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) 4.375 Price of Call C K2 1.5 Price of Put C K1 65 Call Strike Price K 2 55 Put Strike Price K 1 75 Stock Price S T >= K 2 60 Stock Price K 1 < S T < K 2 45 Stock Price S T <= K 1 Example: AT&T (January 1995) - stock price far from strike price 4.125 5.875 10 0 10 S T >= K 2 -5.875 5.875 0 0 0 K 1 < S T < K 2 4.125 5.875 10 10 0 S T <= K 1 Profit Cost Total Payoff Payoff from Put Payoff From Call Range of Stock Price
  • 58.
    Strangle (Buy Put & Call, Same Expiration Dates, Different Strike Prices; K2 > K1) The farther strike prices are apart, the less the downside risk and the farther the stock price has to move for a profit to be realized Advantage   The downside risk if the stock price ends up at a central value is less with a strangle Disadvantage   The stock price has to move farther in a strangle than in a straddle for the investor to make a profit The investor is betting that there will be a large price move, but is uncertain whether it will be an increase or decrease. When is this appropriate?