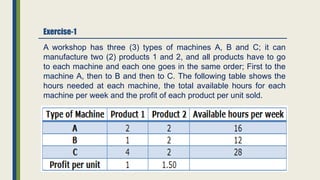
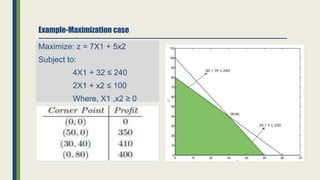
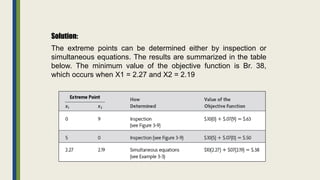
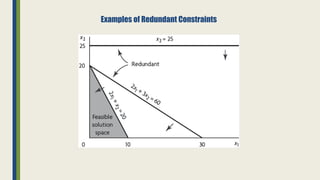
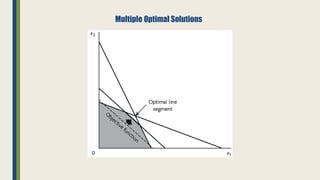
The document discusses linear programming and its key concepts. It begins by defining linear programming as using a mathematical model to allocate scarce resources to maximize profit or minimize cost. It then provides the steps to solve linear programming problems: [1] identify the problem as solvable by LP, [2] formulate a mathematical model, [3] solve the model, and [4] implement the solution. The document also discusses modeling techniques like defining decision variables, objective functions, and constraints. It provides examples of LP formulations and solutions using both graphical and algebraic methods. Finally, it discusses special issues that can arise like infeasible, unbounded, and redundant solutions or the existence of multiple optimal solutions.

1. Chapter Two
Linear Programming
Model Formulation and Solution

2. Definitions of Linear Programming(LP)
• Linear programming uses a mathematical model to find the best allocation of scarce
resources to various activities so as to maximize profit or minimize cost.
• Linear programming is used to find the best (Optimal solution) to a problem that
requires a decision about how best to use a set of limited resources to achieve
objectives.
• Linear Programming is applied for determining the optimal allocation of resources like
raw materials, machines, manpower, etc. by a firm
 The term “Linear Programming” consists of two words as linear and programming. The word
“linear” defines the relationship between multiple variables with degree one. The word
“programming” defines the process of selecting the best solution from various
alternatives.
 Thus, Linear programming is a mathematical model used to solve problems that can be
represented by a system of linear equations and inequalities.
 Both the objective function and the constraints must be formulated in terms of a linear
equality or inequality.

3. 1) Identify problem as solvable by linear programming
2) Formulate a mathematical model
3) Solve the model
4) Implementation
Steps of solving linear programming problems

4. Formulation of mathematical model for LP problems
 The term formulation refers to the process of converting the verbal
description and numerical data into mathematical expressions,
which represents the relationship among relevant decision
variables, objective and constraints
 The basic components of linear programming are
o Objective function
o Decision variables
o Constraints
o Parameters
o Non-negativity constraints

5. Components of LP model…
• Decision Variables – These are the quantities to be determined and
are represented by mathematical symbols (x1,x2,x3…)
 Constraints – refers to limitations on resources like Labour, material,
machine, time, warehouse space, capital, energy, etc.
 Objective function defines the criterion for evaluating the solution.
The objective function may measure the profit or cost that
occurs as a function of the amounts of various products
produced.
 Parameters - numerical coefficients and constants used in the
objective function and constraints.

6. Steps in Formulating LP models
a) Identify the decision variables and assign symbols to them like
x1,x2,x3 & so on
b) Formulate the objective function in terms of the decision variables.
c) Identify and express all the constraints in terms of inequalities in
relation the decision variable.
d) Determine appropriate values for parameters and determine
whether an upper limit(≤), lower limit(≥), or equality(=) is called for.
• ≤ is used if maximum amount of a resource is given (Maximization case)
• ≥ is used if the minimum amount of resource is given (Minimization case)
• = is used if the exact amount of resource is known
e) Add the non-negativity constraints.

8. Linear programming model format

9. Where,
 The cj s are coefficients representing the per unit profit (or cost) of
decision variable
 The aij’s are referred as technological coefficients which represent
the amount of resource used by each decision variable( activity)
 The bi represents the total availability of the ith resource. It is
assumed that bi ≥ 0 for all i. However, if any bi < 0, then both sides
of constraint i is multiplied by –1 to make bi > 0 and reverse the
inequality of the constraint.
 The expression (≤, =, ≥) means that in any specific problem each
constraint may take only one of the three possible forms: (i) less
than or equal to (≤) (ii) equal to (=) (iii) greater than or equal to (≥)

10. Basic assumptions of linear programming model

11. Assumptions of linear programming…
1. Proportionality/ Linearity: any change in the constraint inequalities will have
the proportional change in the objective function. Thus, if the output is doubled,
the profit would also be doubled.
2. Additivity: the total profit of the objective function is determined by the sum of
profit contributed by each product separately. Similarly, the total amount of
resources used is determined by the sum of resources used by each product
separately.
3. Divisibility /continuity: the values of decision variables can be fractions
although fraction values have no sense sometimes
4. Certainty: the parameters of objective function coefficients and the coefficients
of constraint inequalities is known with certainty. Such as profit per unit of
product, availability of material and labor per unit, requirement of material and
labor per unit are known and is given in the linear programming problem.
5. Finite Choices: the decision variables assume non-negative values b/c the
output in the production problem can not be negative.

12. Model Formulation Example-Maximization Case
Suppose a firm produces two products A and B. For producing each
unit of product A, 4 Kg of Raw material and 6 labor hours are
required. While, for the production of each unit of product B, 4 kg of
raw material and 5 labor hours is required. The total availability of
raw material and labor hours is 60 Kg and 90 Hours respectively (per
week). The unit profit of Product A LP is 35 Birr and of product, B is 40
Birr.
 Develop the given problem as linear programing and determine
amount of product A and B should be produced to maximize the
firm’s profit.
Maximize Z = 35x1+ 40x2
Subject to:
4x1 + 4,x2 ≤ 60 (Raw Material Constraint)
6x1, + 5x2 ≤ 90 (Labor Hours Constraint)
x1, x2 ≥ 0 (Non-negativity Constraint)

13. Example –2
maximize Z = 60x1+50x2
Subject to:

14. Model Formulation Example-Minimization Case
Minimize: Z = 60x1 + 80x2
Subject to:
3x1+ 4x2 ≥ 8
5x1 + 2x2 ≥ 11
A house wife wishes to mix two types of food F1 and F2 in such a
way that the vitamin contents of the mixture contain at least 8 units of
vitamin A and 11 units of vitamin B. Food F1 costs Birr 60/Kg and
Food F2 costs Birr 80/kg. Food F1 contains 3 units/kg of vitamin A
and 5 units/kg of vitamin B while Food F2 contains 4 units/kg of
vitamin A and 2 units/kg of vitamin B. Formulate this problem as a
linear programming problem to minimize the cost of the mixtures,
x1, x2 ≥ 0 (Non-negativity Constraint)

15. A workshop has three (3) types of machines A, B and C; it can
manufacture two (2) products 1 and 2, and all products have to go
to each machine and each one goes in the same order; First to the
machine A, then to B and then to C. The following table shows the
hours needed at each machine, the total available hours for each
machine per week and the profit of each product per unit sold.
Exercise-1

16. Exercise-2
ABC private limited company is engaged in the production of power and
traction transformers. Both of these categories of transformers pass
through three basic processes: core preparation, core to coil assembly, and
vapor phase drying. A power transformer costs Birr 50,000 and traction
transformer costs Birr 10,000. The time required in the production of these
two products in terms of hours for each of the processes is as follows.
Power transformer Traction Transformer
Core preparation 75 15
Core to Coil Assembly 160 30
Vapor Phase Drying 45 10
 If the capacities available are 1000, 1500, and 750 machine hours in
each processes respectively, formulate the problem as LP?

17. An investor has 100,000 to invest. The investor has decided to use three
vehicles for generating income: Municipal Bonds, a Certificate Of
Deposit (CD), and a Money Market Account. After reading a financial
newsletter, the investor has also identified several additional restrictions
on the investments:
a) No more than 40 percent of the investment should be in bonds.
b) The proportion allocated to the money market account should be at
least double the amount in the CD.
c) The annual return will be 8 percent for bonds, 9 percent for the CD,
and 7 percent for the money market account. Assume the entire
amount will be invested.
Formulate the LP model for this problem, ignoring any transaction costs
and the potential for different investment lives. Assume that the investor
wants to maximize the total annual return.
Exercise 3-Portfolio Selection

18. Exercise-4
The Bright Paper Company produces three-ring notebook paper in a standard
and small size. Both sizes are produced in the same manufacturing
processes, which consist of steps of cutting the pages, punching three holes,
and wrapping the sheets up in packages of 100. The company measures its
production in packages of 100 sheets. A package of standard paper costs Br.
0.80 to produce and sells for Br. 1.95. A package of small page costs Br. 0.55
to produce and sells for Br. 1.25. All of the production can be sold. The
information on the production system, which consists of two paper cutters,
one punch, and two wrappers is as shown below
Formulate the linear programming version of this problem.

19. Solving Linear Programming Problems
There are generally two methods of solving LPP
a) Graphic method
b) Simplex method

20. The graphical method is limited to LP problems involving two decision
variables and a limited number of constraints due to the difficulty of
graphing and evaluating more than two decision variables.
Important definitions and concepts
a) Solution: A set of decision variables values which satisfy all the constraints
of an LPP
b) Feasible solution: Any solution which also satisfies the non-negativity
limitations of the problem
c) Optimal feasible solution: Any feasible solution which maximizes or
minimizes the objective function
d) Feasible Region: The common region determined by all the constraints
and non-negativity limitations of an LPP
e) Corner point: A point in the feasible region that is the intersection of two
boundary lines
Graphing approach-Extreme Point Solution Method

21. Steps of Graphic Approach
1. Develop an LP model for the given problem
2. Plot constraints on graph paper and decide the feasible region
a) Replace the inequality sign in each constraint by an equality sign and determine the (x1,x2)
coordinates points
b) Draw these straight lines on the graph and decide the area of feasible solutions according to
the inequality sign of the constraint.
c) Shade the common portion of the graph that satisfies all the constraints simultaneously drawn
so far.
d) The final shaded area is called the feasible region (or solution space) of the given lp problem.
Any point inside this region is called feasible solution and this provides values of x1 and x2
that satisfy all the constraints.
3. Examine extreme points of the feasible solution space to find an optimal solution
(a) Determine the coordinates of each extreme point of the feasible solution space.
(b) Compute and compare the value of the objective function at each extreme point.
(c) Identify the extreme point that gives optimal (max. or min.) value of the objective function.

22. Example-Maximization case
Maximize: z = 7X1 + 5x2
Subject to:
4X1 + 32 ≤ 240
2X1 + x2 ≤ 100
Where, X1 ,x2 ≥ 0

23. Exercise
Maximize Z = 3x1  5x2
subject to
x1  4
2x2  12
3x1  2x2  18
and
x1  0, x2  0.
Determine the values of decision variables x1 and x2 that will yield
the maximum profit.

24. Example: Minimization case
Determine the values of decision variables x1 and x2 that will
yield the minimum cost in the following problem.

26. Solution:
The extreme points can be determined either by inspection or
simultaneous equations. The results are summarized in the table
below. The minimum value of the objective function is Br. 38,
which occurs when X1 = 2.27 and X2 = 2.19

27. Exercise
Solve the following linear programming model graphically:

28. Slack versus Surplus
• Slack is the amount of a scarce resource that is unused by a
given solution. It exist in a < constraint.
• Surplus on the other hand is the amount by which the optimal
solution causes a > constraint to exceed the required minimum
amount.
Maximize Z = 60x1+50x2
Subject to:

29. • No Feasible Solutions
• Occurs in problems where to satisfy one of the constraints,
another constraint must be violated.
• Unbounded Problems
• Exists when the value of the objective function can be
increased without limit.
• Redundant Constraints
• A constraint that does not form a unique boundary of the
feasible solution space; its removal would not alter the feasible
solution space.
• Multiple Optimal Solutions
• Problems in which different combinations of values of the
decision variables yield the same optimal value.
Some Special Issues

30. Infeasible Solution: No Combination of x1 and x2, Can
Simultaneously Satisfy Both Constraints
Example: Max Z = 3X1+2X2
Subject to: 2X1 + X2 < 2
3X1 + 4X2 > 12
X1, X2 > 0

31. An Unbounded Solution Space

32. Examples of Redundant Constraints

33. Multiple Optimal Solutions

34. Exercise: Special Issue