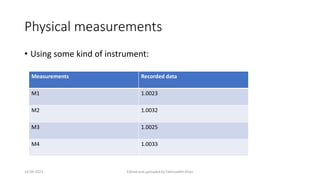
Errors occur in numerical computations due to approximations. Common sources of error include rounding numbers to a certain number of significant figures and truncating infinite series. Absolute error is the difference between the true and approximate values, while relative error is the absolute error divided by the true value. Percentage error expresses relative error as a percentage. Examples show how to calculate absolute, relative, and percentage errors when rounding numbers or truncating functions.

1. Errors in Computation
Fakhruddin Khan
Assistant Professor,
Amity University, Patna
14-09-2021 Edited and uploaded by Fakhruddin Khan

2. Why Error?
• Numerically computed solutions are subject to certain errors, since it
gets approximated up to certain significant digits.
• E.g. 4.200114536---- == 4.2001 , so error arises
• 2/3 = 0.6666666666----------------------infinite. == 0.6667
• 2001 Rs and 10 paise == 2002 Rs (2001Rs + 10paise+ 90paise)
Reason: 10 * 10000 = 100000 paise = 1000 Rs.
14-09-2021 Edited and uploaded by Fakhruddin Khan

3. Significant Digits and Significant figures
Exact Numbers and approximate numbers:
The numbers like 1, 2, 5…. ½ = 0.5 , 3/2= 1.5, are exact numbers
➢Exact numbers are always terminating numbers
The numbers like 2/7 = 0.28571...., 𝜋 = 3.1487. ., e= 2.71828…,
2= 1.414… are approximate numbers.
➢Approximate numbers are non-terminating
14-09-2021 Edited and uploaded by Fakhruddin Khan

4. Contd..
• The digits that are used to express a number are called significant
digits or significant figures.
e.g. 2.3214 has five significant digits
1.1001 has five significant digits
0.04500 has four significant digits etc..
14-09-2021 Edited and uploaded by Fakhruddin Khan

5. Significant Digits and Significant figures
• Rules for finding significant digits
• 1. All non-zero digits are significant
2.12345 six significant digits
23145 Five significant digits
• 2. All zero occurring between non-zero digits are significant.
3.10067 six significant digits
1.000000001 Ten significant digits
500.02 Five significant digits
• 3. Trailing zeros following a decimal points are significant.
3.500, 65.00, 0.3210 All are four significant digits
14-09-2021 Edited and uploaded by Fakhruddin Khan

6. Contd..
• 4. Zeros between the decimal point and preceding non-zero digit are not
significant
0.0123 Three significant digits
0.000001 one significant digits
0.0001234 four significant digits
• 5. When the decimal point is not written, trailing zeros are not considered
to be significant.
4500 = 45 x 102 = Two significant digits
500000 = 5 x 105
= One significant digits
14-09-2021 Edited and uploaded by Fakhruddin Khan

7. Examples:
• Find the number of significant digits:
• 7.560 = Four
• 25000 = Two
• 2.000004 = Seven
• 0.004510 = Four
• 0.0011002 = Five
• 100.000001 = Nine
• 36000 = Two
• 42 x 105
= Two
14-09-2021 Edited and uploaded by Fakhruddin Khan

8. Accuracy & Precision
• Accuracy: It refers to the number of significant digits in a value.
For example, the number 57.396 is accurate to five significant digits.
0.0456000 accuracy is to six significant digits
• Precision: The number of decimal positions.
For example, the number 57.396 has a precision of 0.001 or 10−3
0.001 =
1
1000
= 10−3
14-09-2021 Edited and uploaded by Fakhruddin Khan

9. Example
• Which of the following numbers has the greatest precision.
4.2301 = precision of 10−4
4.23 = precision of 10−2
4.230106 = precision of 10−6
The number 4.230106 has greatest precision.
4.230106 =
4230106
1000000
= 4230106 x 10−6
14-09-2021 Edited and uploaded by Fakhruddin Khan

10. Q.A
• How many significant digits are there in following numbers
• 7.56 x 102 = 756 Three
7.560 x 103 = 7560 Four
14-09-2021 Edited and uploaded by Fakhruddin Khan

11. Rounding off a number to n significant digit
• To round off to n significant digit:
i) If (n+1)th digit is less than 5, leave as it is.
ii) If the (n+1)th digit is greater than 5, add +1 to nth digit.
iii) If the (n+1)th digit is equal to 5, check for nth digit
a) if it is odd, add +1
b) if it is even, leave as it is.
14-09-2021 Edited and uploaded by Fakhruddin Khan

12. • Roundoff to 5 significant digits
• 2.3403674 = 2.340(3+1)= 2.3404; since, (n+1)th digit is > 5
• 2.3403474 = 2.3403; since, (n+1)th digit is < 5
• 2.3403574 = 2.340(3+1) = 2.3404; since, (n+1)th digit is = 5 and
nth digit is odd
• 2.3406574 = 2.3406; since, (n+1)th digit is = 5 and
nth digit is even
14-09-2021 Edited and uploaded by Fakhruddin Khan

13. Examples:
• Round off to four significant digit…
• 7.8926 = 7.893
• 128.614 = 128.6
• 1.70292 = 1.703
• 0.0022431 =0.002243
• 0.700292 = 0.7003
• 2.23457 = 2.234
• 2.23756 = 2.238
14-09-2021 Edited and uploaded by Fakhruddin Khan

14. ERRORS
• When we approximate any number to a certain value or a function up
to certain terms, it produces errors.
Types of errors:
1. Inherent error
ii. Data error also called empirical error
iii. Conversion error
14-09-2021 Edited and uploaded by Fakhruddin Khan

15. Physical measurements
• Using some kind of instrument:
Measurements Recorded data
M1 1.0023
M2 1.0032
M3 1.0025
M4 1.0033
14-09-2021 Edited and uploaded by Fakhruddin Khan

16. Contd..
• 2) Numerical error
i) Round off error : Arises when approximate a number
ii) Truncation error: Arises when approximate a function or equation
14-09-2021 Edited and uploaded by Fakhruddin Khan

17. Absolute, Relative and Percentage Errors
• Absolute Error = 𝐸𝑎 = |X - 𝑋𝑎|
• where X Absolute value / True value
• 𝑋𝑎 is the approximate value
• Relative Error = 𝐸𝑟= It is the ratio of absolute error to the true value.
=
𝐴𝑏𝑠𝑜𝑙𝑢𝑡𝑒 𝐸𝑟𝑟𝑜𝑟
𝑇𝑟𝑢𝑒 𝑉𝑎𝑙𝑢𝑒
=
𝐸𝑎
𝑋
• Percentage Error = 𝐸𝑝= It is the percentage of the relative error
14-09-2021 Edited and uploaded by Fakhruddin Khan

18. Truncation Examples:
• Absolute value =X = 𝑒𝑥 = 1 + x +
𝑥2
2!
+
𝑥3
3!
+
𝑥4
4!
+
𝑥5
5!
+ ------------------------
Infinite
• Approximated value = 𝑋𝑎 = 𝑒𝑥 = 1 + x +
𝑥2
2!
+
𝑥3
3!
• Absolute Error = 𝐸𝑎 = |X - 𝑋𝑎|
14-09-2021 Edited and uploaded by Fakhruddin Khan

19. Example:
• Find the truncation error in the result of the following function for x =
1/5, when first three terms are approx. 𝑒𝑥 = 1 + x +
𝑥2
2!
+
𝑥3
3!
+
𝑥4
4!
+
𝑥5
5!
+
------------------------Infinite
Soln: X = 1 + x +
𝑥2
2!
+
𝑥3
3!
+
𝑥4
4!
+
𝑥5
5!
+ ------------------------Infinite
Xa = 1 + x +
𝑥2
2!
Ea = |X – Xa|=
𝑥3
3!
+
𝑥4
4!
+
𝑥5
5!
=
.23
3!
+
.24
4!
+
.25
5!
=
.008
6
+
.0016
24
+
.00032
120
=
.00133+ .000067 + .0000026 = 0.0014
14-09-2021 Edited and uploaded by Fakhruddin Khan

20. Example:
• Round off the number 1.903527 to four significant digits and find
absolute, Relative and percentage error.
Solution: Absolute Error = 𝐸𝑎 = |X - 𝑋𝑎|
Given, X = 1.903527
𝑋𝑎= 1.904
𝐸𝑎 = |1.903527 – 1.904| = 0.000473
Relative Error = 𝐸𝑟 =
𝐸𝑎
𝑋
=
0.000473
1.903527
= 0.0002485 = 2.485 * 104
Percentage error = 0.02485% = 2.485 * 102
14-09-2021 Edited and uploaded by Fakhruddin Khan

21. Example: Find absolute error, Relative error and percentage
error
The number 2.45789 is rounded off to 5 significant digits.
• Given, X = 2.45789 , 𝑋𝑎 = 2.4579
• Absolute Error = 𝐸𝑎 = |X - 𝑋𝑎| = |2.45789 – 2.4579|
• = 0.00001 = 1* 10−4
• Relative error = 𝐸𝑟 =
𝐸𝑎
𝑋
=
0.00001
2.45789
= 0.00000407 = 4.07 * 10−6
• 𝐸𝑝 =
𝐸𝑎
𝑋
x 100 = 𝐸𝑟 * 100 = 4.07 * 10−4
14-09-2021 Edited and uploaded by Fakhruddin Khan

22. Thank You
14-09-2021 Edited and uploaded by Fakhruddin Khan