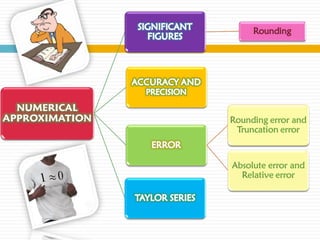
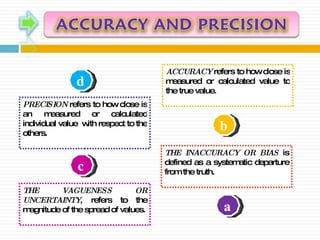
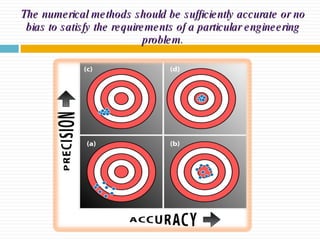
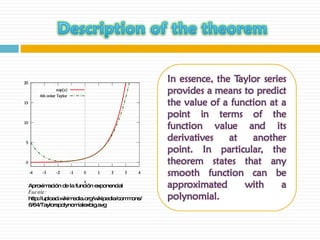
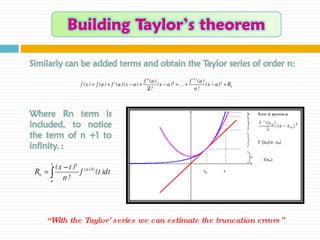
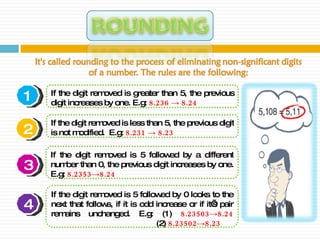
The document discusses significant figures and accuracy in measurements. It explains that: 1) Nonzero digits are always significant, while trailing zeros are only significant if they are after a decimal point. 2) In math operations, the answer should be rounded or truncated to the least number of significant figures in the original values. 3) There are various rules for rounding numbers during calculations to determine whether the last digit should be rounded up or left unchanged based on the value of the digit removed.

5. 1

6. 2

7. 1 All nonzero digits are significant: 1,284 g  Has 4 significant figures 1,2 g  Has 2 significant figures With zeroes, the situation is particularly: 2 Zeroes placed before other digits are not significant. 0.046  Has two significant digits.

8. 4009 kg  Has four significant digits. 3 Zeroes placed between other digits are always significant. 4 Zeroes placed after other digits but behind a decimal point are significant. 7,90  Has three significant digits.

9. 8.200 x 10 3  4 S.F 8.20 x 10 3  3 S.F 8.2 x 1 0 3  2 S.F 5 Zeroes at the end of a number are significant only if they are behind a decimal point. Otherwise, it is impossible to tell if they are significant. For example, in the number 8200, it is not clear if the zeroes are significant or not. The number of significant digits in 8200 is at least two, but could be three or four. To avoid uncertainty, use scientific notation to place significant zeroes behind a decimal point:

10. In math operations, the significant number its in answer should equal to the least number of significant digits in any one of the numbers being multiplied, divided etc. ( 3 S.F) (2 S.F) (4 S.F) (2 S.F)

11. 1 If the digit removed is greater than 5, the previous digit increases by one. E.g: 8.236 -> 8.24 2 If the digit removed is less than 5, the previous digit is not modified. E.g: 8.231 -> 8.23 3 If the digit removed is 5 followed by a different number than 0, the previous digit increases by one. E.g: 8.2353->8.24 4 If the digit removed is 5 followed by 0 looks to the next that follows, if it is odd increase or if it’s pair remains unchanged. E.g: (1) 8.23503->8.24 (2) 8.23502->8.23

13. ACCURACY refers to how close is measured or calculated value to the true value. PRECISION refers to how close is an measured or calculated individual value with respect to the others. THE INACCURACY OR BIAS is defined as a systematic departure from the truth. THE VAGUENESS OR UNCERTAINTY , refers to the magnitude of the spread of values. d b c a

14. The numerical methods should be sufficiently accurate or no bias to satisfy the requirements of a particular engineering problem .

16. For the types of errors, the relationship between the exact or true result and the approximate is given by: True value = Approximation + error

17. Relative Error It is the quotient (division) between the absolute error and the true value. If you multiply by 100 to obtain the true percentage relative error. True or Absolute Error It is equal to the difference between the true value and approximate value or

20. Aproximación de la función exponencial Fuente: http://upload.wikimedia.org/wikipedia/commons/6/64/Taylorspolynomialexbig.svg

23. “ With the Taylor’ series we can estimate the truncation errors”