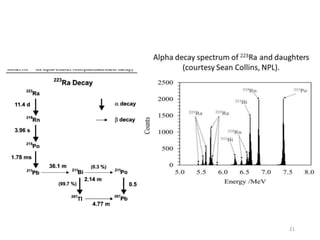
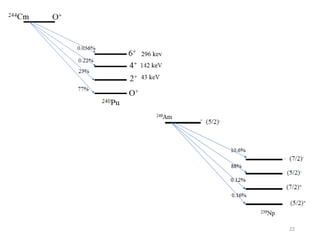
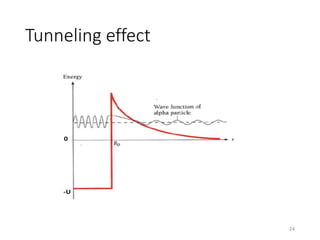
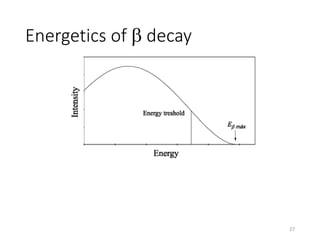
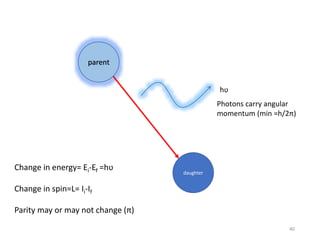
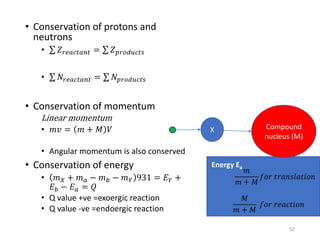
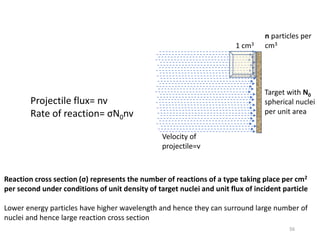
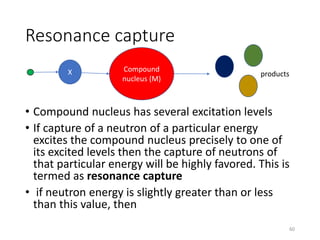
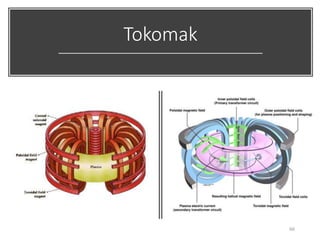
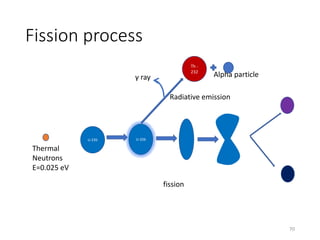
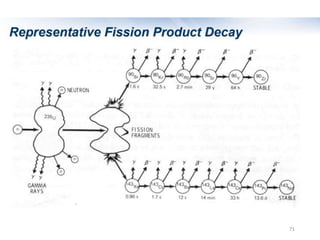
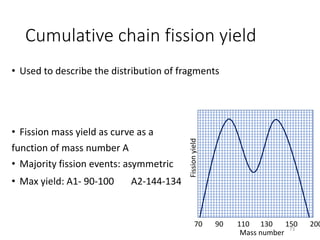
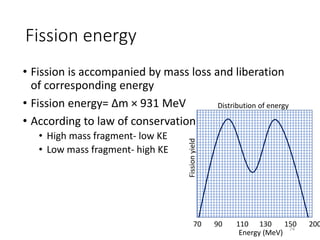
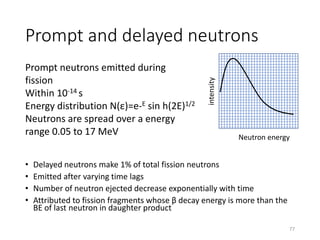
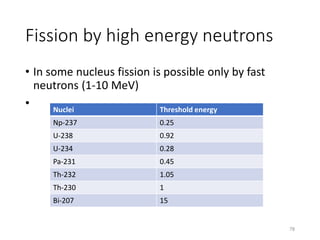
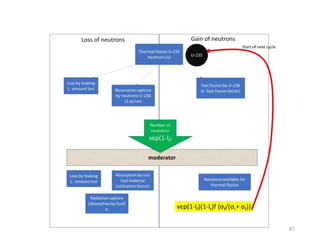
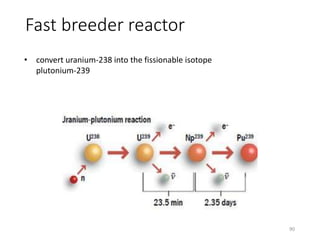
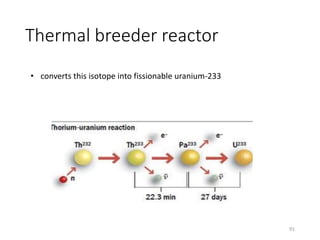
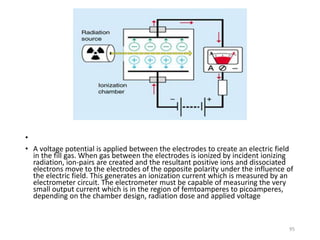
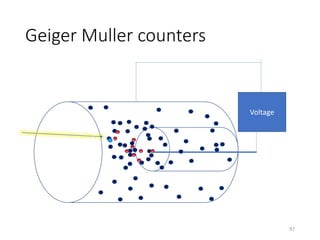
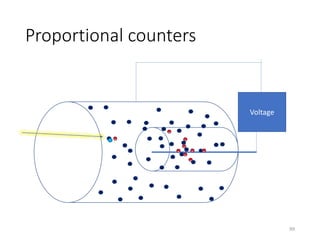
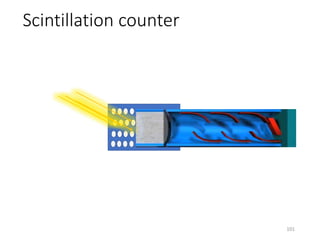
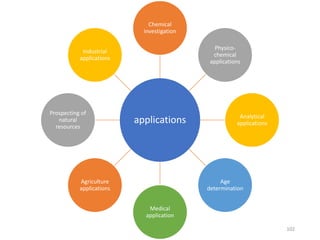
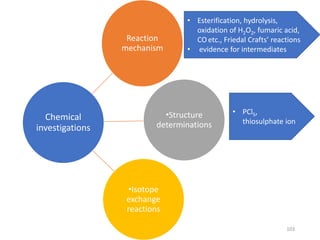
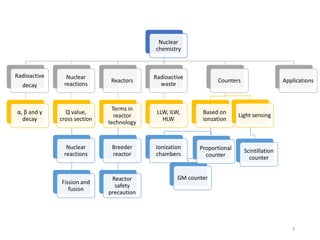
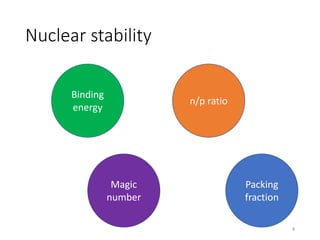
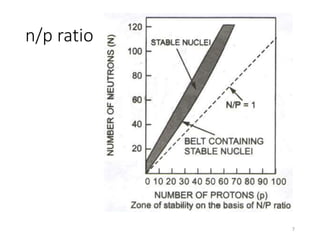
Nuclear chemistry deals with radioactive processes and transformations that occur within atom nuclei. It involves the study of radioactive decay, nuclear reactions, nuclear reactors, radioactive waste management, and applications of radioisotopes. Some key areas covered include alpha and beta decay, nuclear stability factors like binding energy and neutron-to-proton ratio, and nuclear reaction terms such as cross-section and fission.

1. NUCLEAR CHEMISTRY
Nuclear chemistry is the subfield of chemistry dealing with
radioactivity, nuclear processes, and transformations in the
nuclei of atoms.
1

2. Briefly..
• Radioactive decay
• Nuclear reactions
• Nuclear reactors
• Management of radioactive wastes
• Radiation counting techniques
• Application of radioisotopes
2

3. Nuclear
chemistry
Radioactive
decay
α, β and γ
decay
Nuclear
reactions
Q value,
cross section
Nuclear
reactions
Fission and
fusion
Reactors
Terms in
reactor
technology
Breeder
reactor
Reactor
safety
precaution
Radioactive
waste
LLW, ILW,
HLW
Counters
Based on
ionzation
Ionization
chambers
GM counter
Proportional
counter
Light sensing
Scintillation
counter
Applications
3

4. Nuclear stability
Binding
energy
n/p ratio
Packing
fraction
Magic
number
4

5. Binding energy
• the energy that holds a nucleus together. This is
equal to the mass defect of the nucleus.
• 𝐸 = Δmc2
• 𝐸 = ∆𝑚 × 931 MeV
• 1 amu = 931 MeV
5

6. Significance of BE
• Nuclear binding energy is the energy required to
split a nucleus of an atom into its components.
• Nuclear binding energy is used to determine
whether a process will be favorable.
6

7. n/p ratio
7

8. Radioactive Decay
• Radioactive decay
• the process by which an unstable atomic nucleus loses
energy (in terms of mass in its rest frame) by emitting
radiation
• such as
• alpha particle
• beta particle with neutrino or only a neutrino in the case
of electron capture, or a gamma ray or electron in the
case of internal conversion
8

9. Kinetics
Radioactive decay law
• If N radioactive nuclei are present at time t and if no
new nuclei are introduced into the sample, then the
number dN decaying in a time dt is proportional to N
and so
𝜆 = −
(
𝑑𝑁
𝑑𝑡
)
𝑁
Integrating, we get the exponential law of radioactive
decay.
𝑁 = 𝑁0 𝑒−𝜆𝑡
• Where N0 is the number of nuclei present at time t=0.
9

10. RADIOACTIVE DECAY
• Decay series
• Alpha decay
• Beta decay
• Gamma decay
10

11. Radioactive Decay
• Energetics
• Range
• Theory of decay: how it happens
11

12. Energy and Range: ionization
power
• Can be found by measurement of their absorption
by medium
• Knowledge of interaction with absorption medium
tells us idea about the range of the emitted
radiation
12

13. Alpha decay
• Parent nucleus emit α particle producing a daughter nucleus of four mass units
less and charge two units less
• 𝑍
𝐴
𝑋 → 𝑍−2
𝐴−4
𝑌 + 2
4
𝐻𝑒
• Reason : nucleus with 210 or more nucleons is so large that the nuclear force
holding them together barely counterpart the electromagnetic repulsion
between protons.
• Why alpha decay?
• Average BE of last 4 nucleon= 7MeV
• so net of 28 MeV required to remove them separately.
• BE released upon formation of 1 alpha particle= 28.3 MeV
• Hence favorable process.
13

14. Alpha decay
• Energy
• Range
• Spectra
• Theory of alpha decay
14

15. Energy of alpha particle
• The maximum energy available for alpha particle is
equivalent to the mass defect
𝐸 = [𝑚𝑝 − (𝑚𝑟 + 𝑚α)] 931 MeV
• 𝑚 𝑝- mass of parent nucleus
• 𝑚 𝑟- mass of daughter (recoil) nucleus
• 𝑚α− mass of alpha particle
• E= Er +Eα
15

16. Range of alpha particles:
• it is the distance in air from source to a point within which the
emitted alpha particles produce ionization and beyond which
their ionization power ceases.
• The value of ranges are measured at 150C in air at 1 atm
pressure.
• As the distance of the alpha particles from the source increases
the specific ionization increases at first slowly and then more
rapidly, reaches a maximum and then falls rapidly and finally
decreases somewhat more slowly to zero. 16

17. Straggling effect:
• alpha particle emitted from a given source lose a large fraction of their energy by
causing ionization of air along their path.
• Extend of ionization depends on the number of particles they encounter on their
path and the way they encounter.
• All alpha particles will not lose their energy in an equal way.
• Some may not convert to neutral atom. Some may exist as He+.
• Cause a slight variation in the range and hence a point of inflation is observed in the
curve.
• This variation is referred to as straggling. Because of straggling, the actual range of
alpha particles is not definite and hence extrapolated range is considered.
17

18. Energy –
from range of alpha particle
• Range – energy relationship:
• The mean range in air is related to the energy E of
the particle by the relation
• 𝑅 = 0.318𝐸3/2
18

19. Geiger – Nuttal rule:
• Energy – disintegration constant relation
• it states that short-lived isotopes emit more energetic alpha particles than long-
lived ones
• When the logarithm of the disintegration constant λ (sec-1) is plotted against the
logarithm of range R0 (cm) of the emitted alpha particles, a linear plot will be
obtained for a given radioactive series.
• 𝒍𝒐𝒈 𝝀 = 𝒂 𝒍𝒐𝒈 𝑹 𝟎 + 𝒃
• Considering the range- energy relationship of the alpha particle, Geiger- Nuttal
rule may be written in the form
• 𝒍𝒐𝒈 𝝀 = 𝒂′ 𝒍𝒐𝒈 𝑬 𝟎 + 𝒃 ′
• a’ and b’ are constants for a radioactive series.
19

20. Alpha decay spectra
• According to law of conservation of momentum
• Ermr = Eαmα
• When observed with spectrograms of high resolution,
alpha decay spectra shows few sharp monoergic lines
BE ≡ KE available for alpha particle
20

21. 21

22. 22

23. Alpha decay theory
• The wave mechanical theory
• preformation of alpha particles in the nucleus
• Once the alpha particle is formed, it moves towards the boundary
of the nucleus.
• This alpha particle will be repelled at the nuclear potential
boundary.
• It will oscillate inside the potential well if the KE of the alpha
particle is less than zero the nucleus will be stable and there will
not be an alpha emission.
• If the energy is greater than zero, the particle will move towards the
boundary of the potential well, collides with it and tends to escape
from the nuclear potential boundary (potential barrier).
• alpha particles will not necessarily cross over the barrier but
may leak through and proceed in its forward direction. This
barrier penetration of alpha particles is called tunnel effect
23

24. Tunneling effect
24

25. Beta decay
• Types
• Energy
• Range
• Spectra
• Theory of decay
25

26. TYPES OF b DECAY
Type Energy released Process
Example
b- Decay E = Δmc2 𝑛 → 𝑝 + β− + 𝑎𝑛𝑡𝑖𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜
11
24
𝑁𝑎 → 12
24
𝑀𝑔 + β− + 𝑎𝑛𝑡𝑖𝑛𝑢𝑡𝑟𝑖𝑛𝑜
b+ Decay E = Δmc2 -2me 𝑝 → 𝑛 + β+
+ 𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜
11
24
𝑁𝑎 → 10
22
𝑁𝑒 + β+
+ 𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜
Electron
capture
E = Δmc2 –BEcaptured electron 𝑝 + 𝑒 → 𝑛 + 𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜
26
55
𝐹𝑒 → 25
55
𝑀𝑛 + 𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜
26

27. Energetics of b decay
27

28. Absorption of b particles and their
range through matter
• Emax found out by absorption measurements
• The maximum range for a beta particle spectrum may be obtained
from an experimental absorption curve
• By visual inspection
• Feather plot (absorption curve is compared with absorption
curve of a standard beta emitter)
Range energy relation:
Empirical relations have been proposed
𝑅 = 0.543𝐸 − 0.160
• E- maximum energy
• Valid for 0.6MeV – 15MeV
28

29. Explanation for b+ decay
• Dirac theory
• n/p ratio
29

30. 1. Dirac theory – b+ decay
• Dirac’s relativistic theory:
both positive and negative energies are possible for electrons
𝐸 = ± 𝑝2 𝑐2 + 𝑚 𝑒
2
𝑐4
• For each positive energy state there will be a negative state
30

31. 1. Dirac theory – b+ decay
2mec2
+mec2
-mec2
1.02 MeV
• All negative states are filled : there is no
vacancy
• Vacancy can be created in the negative
state if a high energy photon interact with
matter and left an electron out to one of
the vacant positive energy state.
• This electron behave as an ordinary
electron and the vacancy will behave as a
positron (electron with positive charge)
• For electron hole pair to be produced, the
photon must have an energy of 1.02 MeV
31

32. Condition for b+ decay
• Energy needed = 1.02 MeV ≡ 2𝑚 𝑒 𝑐2
(2 × 9.10938356 × 10-31 × (3 × 108)2)
• Mass defect Δm≥ 2𝑚 𝑒
𝑚 𝑧 − 𝑚 𝑧−1 ≥ 2𝑚 𝑒
𝑚 𝑧 − (𝑚 𝑧−1+2𝑚 𝑒) > 0
Energy (𝑚 𝑧−(𝑚 𝑧−1+2𝑚 𝑒))931 = 𝐸𝑒 + 𝐸 𝑣
32

33. Electron-positron annihilation
• Low energy: (0.51 MeV) electron and positron
collide to form γ ray photon
𝑒−
+ 𝑒+
→ 𝛾
• High energy: other particles such as mesons,
bosons etc. will be formed.
33

34. Electron capture
𝑍
𝐴
𝑋 → 𝑍−1
𝐴
𝑌 + 𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜
Δm𝑐2
≥ 𝐸 𝑏
Eb= 𝑏𝑖𝑛𝑑𝑖𝑛𝑔 𝑒𝑛𝑒𝑟𝑔𝑦 𝑜𝑓 𝑒𝑙𝑒𝑐𝑡𝑟𝑜𝑛 𝑖𝑛 𝑡ℎ𝑒 𝑠ℎ𝑒𝑙𝑙
Δm = (Mx- My)
34

35. Energy condition for b decay
Type Energy released
b- Decay 0≤ Δm
b+ Decay 0 ≤1.02≤Δm 931
Electron
capture
0 ≤BE captured electron≤ E = Δmc2 931
35

36. Double b decay
• Process in which an initial nuclei 𝑍
𝐴
𝑋 𝑑𝑒𝑐𝑎𝑦𝑠 𝑡𝑜 𝑍+2
𝐴
𝑌 emitting 2
electrons and 2 antineutrinos
• 𝑍
𝐴
𝑋 → 𝑍+2
𝐴
𝑌 + 2𝑒− + 2 𝑎𝑛𝑡𝑖𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜𝑠
• Typical double b decay is an even even nucleus 𝑍
𝐴
𝑋 whose BE is
more than its neighbor but less than the 𝑍+2
𝐴
𝑌
• 32
76
𝐺𝑒 → 34
76
𝑆𝑒 + 2𝑒−
+ 2 𝑎𝑛𝑡𝑖𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜 (double b decay)
32
76
𝐺𝑒 → 33
76
𝐴𝑠 + 𝑒−
+ 𝑎𝑛𝑡𝑖𝑛𝑒𝑢𝑡𝑟𝑖𝑛𝑜 (b decay)
b+ decay will also occur in the similar way
36

37. • After any radioactive process, there is a chance to
find daughter nucleus in exited state
• Deexcitation can occur as
• Photon emission/ γ decay
• Ejection of electrons from outer orbitals
37

38. Gamma decay
• Usually spin and parity of parent and daughter
nuclei indicated
• Probability of γ transition governed by reduced
transition probability
• reduced transition probability depends on the
wavefunctions of initial and final states i.e., the spin
and parity of parent and daughter
38

39. Based on t1/2 value gamma
transitions are termed as
1. instantaneous transitions: τ< 10-7s
2. isomeric transitions: τ > 10-7s (occur between metastable
and ground state)
Every permitted atomic nucleus is a quantum state
characterized by definite energy (E), spin (I) and
parity (π)
39

40. parent
daughter
Change in energy= Ei-Ef =hʋ
Change in spin=L= Ii-If
Parity may or may not change (π)
hʋ
Photons carry angular
momentum (min =h/2π)
40

41. Nucleus- photon interaction
• Results in
• To and fro motion of charges gives rise to electric
multipole radiation (EL)
• Fluctuation of the electric current flowing in closed
loops: magnetic multipole radiation (ML)
• Here L indicate the difference between initial and
final spin states 𝐼𝑖 − 𝐼𝑓
41

42. Whether ML or EL?
• 𝜋𝑖 + 𝜋 𝑓 + 𝐿 (Even parity is counted as +1 and odd parity as 0)
Sum
𝝅𝒊 + 𝝅 𝒇 + 𝑳
evenoddML EL
Process
Parity
Spin (L)
Sum
𝝅𝒊 + 𝝅 𝒇 + 𝑳
Type of
decayinitia
l
Final
1 1 1 Even Even EL
2 0 0 Odd Odd ML
3 0 1
Even Odd ML
4 1 0
5 0 1
Odd Even EL
6 1 0 42

43. Isomeric transitions
• Decay life time > 10-7s
• Nuclear isomers: nuclides with same Z and A but
differ in their energy state, spin in some cases parity
• Parent isomer: metastable state ( due to large
difference spin between initial and final state L≥ ±3)
43

44. Internal conversion
• Alternative to γ emission
• Transition of an excited nucleus to ground state by
ejection of orbital electrons
• Energy and angular momentum
changes are transferred to orbital
electrons
• Transferred energy must be higher than
binding energy of electron
• KE of electron Ee= Eγ-Eb
• Eγ – energy difference between initial
and final states
• Eb – binding energy of electron
44

45. • These conversion electrons display an energy spectrum
consisting of discrete lines
E1 = Eγ-EK
E2 = Eγ-EL1
E3 = Eγ-EL2
E4 = Eγ-EL3
• Total decay constant is λ=λ γ+ λ K+ λ L+…
• Conversion coefficient
α =
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑐𝑜𝑛𝑣𝑒𝑟𝑠𝑖𝑜𝑛 𝑒𝑙𝑒𝑐𝑡𝑟𝑜𝑛𝑠 𝑝𝑒𝑟 𝑢𝑛𝑖𝑡 𝑡𝑖𝑚𝑒
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑝ℎ𝑜𝑡𝑜𝑛𝑠 𝑝𝑒𝑟 𝑢𝑛𝑖𝑡 𝑡𝑖𝑚𝑒
Representing electrons ejected from
K(1s1/2), L1(2s1/2), L2(2p1/2), L3(2p3/2)
45

46. • During internal conversion and electron capture,
vacancies are created in the inner orbitals
• The process of vacancy filling can be through
• Radiation emission
• Electron emission (auger effect)
46

47. Radiation emission
• An electron jump to an inner vacancy
• Radiation will be emitted
• Energy of radiation 𝐸 = 𝐸 𝐵1 − 𝐸 𝐵2
• Vacancy is pushed outward
• Leads the atom to +1 state
M
1+
47

48. Auger effect
Non-radiative energy
transfer
• Inner vacancy is filled by electrons in higher orbitals
• Excess energy is non radiatively transferred to electrons in higher levels.
• Electrons get ejected out
• The kinetic energy of ejected electron= 𝐸 = 𝐸 𝐵1 − (𝐸 𝐵2 + 𝐸 𝐵3)
EB1 – binding energy of innermost electron
EB2 – binding energy of electron which jumped into the inner orbital
EB3 – binding energy of ejected electron
The process of ejection of electron
can go on as long as the E is +ve
Auger effect is a physical phenomenon in
which the filling of an inner-shell vacancy of
an atom is accompanied by the emission of
an electron from the same atom.
48

49. Nuclear reactions
• Process in which a nucleus reacts with another
nucleus, an elementary particle or a photon to
produce in a time of order of 10-12 sec or less one
or more other nuclei.
• 𝑍1
𝐴1
𝑋 + 𝑍2
𝐴2
𝑎 → 𝑍3
𝐴3
𝑌 + 𝑍4
𝐴4
𝑏
Target projectile recoil ejectile
• Representation
𝑍1
𝐴1
𝑋 𝑎, 𝑏 𝑍3
𝐴3
𝑌
49

50. Types
• Elastic scattering
• Inelastic scattering
• Photonuclear reactions
• Radiative capture
• Other types
• Special nuclear reactions
50

51. Energetics of nuclear reactions
• Accompanied by release or absorption of energy
• Expressed by term ‘Q value’
• 𝑄 = ∆𝑚 × 931 𝑀𝑒𝑉
• Barriers
• Columbic interaction (columbic barrier)
• Charged particle
• Provide the minimum energy requirement
• Angular momentum interaction (centrifugal barrier)
• Due to interaction of angular moments of projectile and target
• Keeps any projectile at
𝑙
2𝜋
de brouglie wavelength from target
51

52. • Conservation of protons and
neutrons
• 𝑍 𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡 = 𝑍 𝑝𝑟𝑜𝑑𝑢𝑐𝑡𝑠
• 𝑁𝑟𝑒𝑎𝑐𝑡𝑎𝑛𝑡 = 𝑁𝑝𝑟𝑜𝑑𝑢𝑐𝑡𝑠
• Conservation of momentum
Linear momentum
• 𝑚𝑣 = 𝑚 + 𝑀 𝑉
• Angular momentum is also conserved
• Conservation of energy
• 𝑚 𝑋 + 𝑚 𝑎 − 𝑚 𝑏 − 𝑚 𝑌 931 = 𝐸 𝑌 +
𝐸 𝑏 − 𝐸 𝑎 = 𝑄
• Q value +ve =exoergic reaction
• Q value -ve =endoergic reaction
X Compound
nucleus (M)
𝑚
𝑚 + 𝑀
𝑓𝑜𝑟 𝑡𝑟𝑎𝑛𝑠𝑙𝑎𝑡𝑖𝑜𝑛
𝑀
𝑚 + 𝑀
𝑓𝑜𝑟 𝑟𝑒𝑎𝑐𝑡𝑖𝑜𝑛
Energy Ea
52

53. Threshold energy
• Exergonic reaction: depends on barrier (a minimum
threshold exist)
• Endergonic reaction: a minimum of Q amount of energy is
needed – obtained from the kinetic energy of the projectile
• 𝑍1
𝐴1
𝑋 + 𝑍2
𝐴2
𝑎 → 𝑍3
𝐴3
𝑌 + 𝑍4
𝐴4
𝑏
For reaction to be possible
𝐸 𝑎 ≥ 1 +
𝑀
𝑚
𝑄
𝑄 ≤ 1 +
𝑚
𝑀
𝐸 𝑎
Ea KE of projectile
m- mass of projectile
M- mass of compound nucleus 53

54. How much energy needed for a
projectile??
• 𝑁14
(𝛼, 𝑝)𝑂17
:
• α is charged particle: there is columbic barrier
• Q value is -1.20MeV.
Reaction will not occur if α particle of KE 1.20 MeV is used
When KE =1.20 MeV; Ea= 𝑀/(𝑀 + 𝑚) 𝑄 =14/18 = 0.77
MeV will be available for reaction. reaction will not occur.
For reaction to occur Ea = ((M+m)/M )Q = 18/14= 1.54
MeV is the required KE of the projectile.
54

55. Nuclear reaction Cross section (σ)
• Probability of a nuclear reaction
• Expressed in barns (b)
• 1 b= 10-28 m = 100 fm
• σi – i represent the type of nuclear reaction
• It represents the number of reactions of a type
taking place per cm2 per second under conditions
of unit density of target nuclei and unit flux of
incident particle.
55

56. Target with N0
spherical nuclei
per unit area
n particles per
cm31 cm3
Velocity of
projectile=v
Projectile flux= nv
Rate of reaction= σN0nv
Reaction cross section (σ) represents the number of reactions of a type taking place per cm2
per second under conditions of unit density of target nuclei and unit flux of incident particle
Lower energy particles have higher wavelength and hence they can surround large number of
nuclei and hence large reaction cross section
56

57. Reaction cross section
• Energy of projectile
• Nature of target nuclei
• Flux of projectile
*
• If energy of projectile is very low, it may not be
possible to overcome the barriers
• Too high energy of projectile can decrease the cross
section
57

58. Variation of neutron capture cross
section with energy (1/v law)
• Neutron capture: no columbic barrier
• Slow neutron capture cross section varies inversely
with the neutron velocity : 1/v law
• Neutron capture cross section (σ) varies as the
square root of neutron energy
Since v= 2𝑚𝐸
Log(σ)barns
Log (neutron energy) eV 58

59. Resonance capture
• According to 1/v law, slow neutron capture cross section
area should decrease with velocity of neutron.
But
• In many cases, beyond a limit, the curve for the 1/v law gets
superimposed by sharp peaks at definite values of neutron
energy. These peaks are known as resonance captures
σ(barns)
neutron energy (eV)
59

60. Resonance capture
• Compound nucleus has several excitation levels
• If capture of a neutron of a particular energy
excites the compound nucleus precisely to one of
its excited levels then the capture of neutrons of
that particular energy will be highly favored. This is
termed as resonance capture
• if neutron energy is slightly greater than or less
than this value, then
X Compound
nucleus (M)
products
60

61. Photonuclear reactions
• Interaction of a high energy photon with a nucleus
• Types:
(γ, γ’) reaction (excitation of nucleus followed by de-
excitation by radiation emission.
(γ, n), (γ, p) and (γ, 2n) reaction High energy is concentrated on a proton or a
neutron. When the value exceeds the
separation energy that nucleon will be emitted
(γ, α) reaction
(γ, m) reaction Photon capture and multiple evaporation
fragmentation Photon capture and then fragmentation
61

62. Features
• Careful measurement of photon energy for (n, γ)
reaction gives the binding energy of the last
neutron in a nucleus
• (n, γ) reactions give monoergic neutrons
62

63. Nuclear Fusion:
Thermonuclear reactions
• Two light nuclei fuse into a single heavy nucleus by
a collision of the two interacting particles at
extremely high temperatures, with the consequent
release of a large amount of energy
• 41
1
𝐻 → 2
4
𝐻𝑒 + 2𝛽+
+ 2ʋ + 26.7𝑀𝑒𝑉
• Naturally occurs in stars
• Mechanism:
• proton-proton chain
• Carbon-nitrogen cycle
63

64. Fusion reactors
• For commercial production of electricity
• Hydrogen fusion reactors
• Fuel: 1
1
𝐻- to bring about reactions as those occur in stars
deuterium, tritium practically used due to the
larger reaction cross section and much lower
threshold temperature
1
2
𝐻 + 1
3
𝐻 → 2
4
𝐻𝑒 + 𝑛 + 𝛾 (energy= 17.6 MeV)
• hurdles on developing a fusion reactor:
1. attain high temperatures as 20-100 MK (as those in
stars)
2. Confine the reaction in suitable structure
64

65. Magnetic confinement
65

66. Tokomak
66

67. Inertial confinement
67

68. NUCLEAR FISSION REACTION
Nuclear fission is a process in which the nucleus of an atom splits into
two or more smaller nuclei as fission products, and usually some by-
product particles.
Thermal neutron
68

69. Theory and process
• Explained using liquid drop model
• Nucleus : incompressible liquid whose size is proportional to
number of nucleons (A)
• Shape is determined by coulomb force and surface tension
• When excited by neutron capture or other process,
• if excitation energy is not high enough, the nucleus revert
back to initial state by radiative decay or by emission of
particles such as α.
• If excitation energy is high enough it may undergo fission
RADIATIVE CAPTURE
69

70. Fission process
U-235
Thermal
Neutrons
E=0.025 eV
U-326
Th -
232
Alpha particle
Radiative emission
γ ray
fission
70

71. 71

72. Fission fragments
• Fission fragments F1 and F2 are not unique pairs
• About 30 possibilities
• F1- A= 85-105
• F2- A= 150-130
• After fission fragments will undergo β emission
since they have excess neutron (high n/p ratio)
• Asymmetry is favored
• Similar masses
• Least probable
• -Only when the neutron energy is high
117-117
100-134
95-139
90-144
72

73. Cumulative chain fission yield
• Used to describe the distribution of fragments
• Fission mass yield as curve as a
function of mass number A
• Majority fission events: asymmetric
• Max yield: A1- 90-100 A2-144-134
70 90 110 130 150 200
Fissionyield
Mass number
73

74. Fission energy
• Fission is accompanied by mass loss and liberation
of corresponding energy
• Fission energy= Δm × 931 MeV
• According to law of conservation of energy,
• High mass fragment- low KE
• Low mass fragment- high KE
70 90 110 130 150 200
Fissionyield
Energy (MeV)
Distribution of energy
74

75. Fission Cross Section and
Threshold
• Possibilities
• (n,n) type reaction (scattering)
• Radiative capture
• Fission
Fission cross section is the measure of the probability of
fission reaction.
It depends on
• Critical size of material
• Threshold energy of neutrons required
75

76. Fission neutrons
• During fission the fissioning nucleus ejects 2-3
neutrons directly at the moment of fission
• For U-235 the fission reaction may be written as
𝑈235 + 𝑛 𝑡ℎ𝑒𝑟𝑚𝑎𝑙
→ 𝑈236 → 𝑋 + 𝑌 + 𝑣𝑛( 𝑓𝑎𝑠𝑡 𝑛𝑒𝑢𝑡𝑟𝑜𝑛𝑠)
V- average number of neutrons in each process
Net number of neutrons emitted per neutron used
up= η=
𝑣σ 𝑓
σ 𝑓+σ 𝑟
σ 𝑓 − 𝑐𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛 𝑓𝑜𝑟 𝑓𝑖𝑠𝑠𝑖𝑜𝑛
σ 𝑟 − 𝑐𝑟𝑜𝑠𝑠 𝑠𝑒𝑐𝑡𝑖𝑜𝑛 𝑓𝑜𝑟 𝑟𝑎𝑑𝑖𝑎𝑡𝑖𝑣𝑒 𝑐𝑎𝑝𝑡𝑢𝑟𝑒
76

77. Prompt and delayed neutrons
• Delayed neutrons make 1% of total fission neutrons
• Emitted after varying time lags
• Number of neutron ejected decrease exponentially with time
• Attributed to fission fragments whose β decay energy is more than the
BE of last neutron in daughter product
Prompt neutrons emitted during
fission
Within 10-14 s
Energy distribution N(ε)=e-E sin h(2E)1/2
Neutrons are spread over a energy
range 0.05 to 17 MeV Neutron energy
intensity
77

78. Fission by high energy neutrons
• In some nucleus fission is possible only by fast
neutrons (1-10 MeV)
• Nuclei Threshold energy
Np-237 0.25
U-238 0.92
U-234 0.28
Pa-231 0.45
Th-232 1.05
Th-230 1
Bi-207 15
78

79. A nuclear chain reaction occurs
when one single nuclear
reaction causes an average of
one or more subsequent nuclear
reactions, thus leading to the
possibility of a self-propagating
series of these reactions.
Nuclear chain reactions are series of nuclear fissions (splitting of atomic nuclei),
each initiated by a neutron produced in a preceding fission. For example, 2.5
neutrons on the average are released by the fission of each uranium-235 nucleus
that absorbs a low-energy neutron.
nuclear chain reaction
79

80. Critical size
The critical size of a system containing a fissile material is defined as the
minimum size in which at least one neutron is available for further fission
reaction. Fission chain reaction is not possible if the size is less than
critical size.
The mass of fissile material at the critical size is called critical mass.
80

81. Fertile and fissile materials
• Fissionable: one capable of undergoing fission
U-235, U-238, Pu-239, Th-232
• Fissile material: one that can
sustain fission chain reaction by thermal neutrons
U-235, Pu-239
• Fertile material: not itself undergo
Sustained chain reaction but can be converted to
fissile material
U-238, Th-232
Fertile
U-238
Th-232
Fissile
U-235
Pu-239
81

82. NUCLEAR REACTOR
A nuclear reactor is a system that contains and controls sustained
nuclear chain reactions. Reactors are used for generating electricity,
moving aircraft carriers and submarines, producing medical isotopes
for imaging and cancer treatment, and for conducting research.
82

83. The reactor core generates heat in a number of ways:
 The kinetic energy of fission products is converted to thermal energy
when these nuclei collide with nearby atoms.
 The reactor absorbs some of the gamma rays produced during fission and
converts their energy into heat.
 Heat is produced by the radioactive decay of fission products and
materials that have been activated by neutron absorption. This decay
heat-source will remain for some time even after the reactor is shut
down.
83

84. COMPONENTS OF A NUCLEAR REACTOR AND REACTOR CONTROL
1. Core: Part of reactor containing fuel elements (fissile U-235, U-233, Pu239
etc.). Fuel elements are made of plates, or rods of Uranium metal or
ceramic, which are usually clad in a thin sheath of SS, Zirconium or
aluminium to provide corrosion resistance, retention of radioactivity and
structural support.
2. Core moderator: commonly water (H2O or D2O) or graphite is dispersed
between the fuel assemblies to moderate or slow down fast neutrons
produced during fission.
3. Control rods: Made of neutron absorbing materials (B, Cd, Ag and In)upon
movement in or out of the core, vary the number of neutrons available for
chain reactions.
4. Reflector: surround the core to reduce the loss of the neutrons. Graphite,
light water and beryllium is used as reflector.
5. Coolant: the heat generated as a result of fission is removed by circulation
of coolant through the core. Coolant used should have high BP, low MP
and should be resistant to corrosion. CO2, H2O, molten Na, mercury etc are
used as coolant.
6. Radiation shielding / biological shielding: for preventing the radiation
hazard.
84

85. 1. Each fission reaction releases large amount of energy
2. Each fission results in an average of 2.5 neutrons (in case of U-235)
Mainly 2 characteristics of fission reaction are of great importance:
• A portion of these neutrons may be absorbed by other fissile atoms and
trigger further fission events, which release more neutrons, and so on.
This is known as a nuclear chain reaction.
• In nuclear reactors, this chain reaction will proceed in a constant rate by
controlling the chain propagation
Sustained chain reaction: the key
85

86. Its all controlling the number of neutrons!!
• In a nuclear reactor, self-sustaining chain reaction takes place.
• The neutrons produced per fission event must be large enough to sustain
the chain reaction, despite the loss of neutrons due to leakage and by
absorption in non-fissile materials.
• The rate of fission reactions within a reactor core can be adjusted by
controlling the quantity of neutrons that are able to induce further fission
events.
86

87. 87

88.  If a system is critical, the multiplication factor is 1.
Signifies a steady state
Number of neutrons and fissions is constant from cycle to cycle
Amount of energy output in unit time is constant
 Supercritical systems have multiplication factors greater than 1
Signifies a divergent state
Number of neutrons, fissions and energy output rapidly increase from
cycle to cycle
Ends up in explosion
 subcritical systems have multiplication factors lesser than 1.
Signifies a convergent state
Number of neutrons, fissions and energy output diminish from cycle to
cycle
Reactor soon gets quenched 88

89. Breeder Reactor
• A Breeder Reactor is a nuclear reactor that
"breeds" fuel.
• Types
• Fast breeder reactor
• Thermal breeder reactor
89

90. Fast breeder reactor
• convert uranium-238 into the fissionable isotope
plutonium-239
90

91. Thermal breeder reactor
• converts this isotope into fissionable uranium-233
91

92. Fast Breeder Test Reactor
• breeder reactor located at Kalpakkam, India.
• The Indira Gandhi Center for Atomic Research
(IGCAR) and Bhabha Atomic Research
Centre (BARC) jointly designed, constructed, and
operate the reactor.
• The reactor uses a plutonium-uranium mixed
carbide fuel and liquid sodium as a coolant.
92

93. Counting techniques
• Ionization chambers
• Geiger muller counters
• Proportionality counters
• Scintillation counters
93

94. Ionization chambers
• the simplest of all gas-filled radiation detectors
• detection and measurement of certain types of
ionizing radiation; X-rays, gamma rays, and beta
particles
• only uses the discrete charges created by each
interaction between the incident radiation and the
gas
• good uniform response to radiation over a wide
range of energies
• Cannot distinguish between radiations
94

95. •
• A voltage potential is applied between the electrodes to create an electric field
in the fill gas. When gas between the electrodes is ionized by incident ionizing
radiation, ion-pairs are created and the resultant positive ions and dissociated
electrons move to the electrodes of the opposite polarity under the influence of
the electric field. This generates an ionization current which is measured by an
electrometer circuit. The electrometer must be capable of measuring the very
small output current which is in the region of femtoamperes to picoamperes,
depending on the chamber design, radiation dose and applied voltage
95

96. GM counter
• Works on the principle of indirect ionization
• Can detect alpha, beta or gamma radiation
• Requires very high voltage for working
• Cannot detect uncharged particles
• Independent of energy of incident particle
96

97. Geiger Muller counters
Voltage
-
- -
-- --
-
-
97

98. Proportional counters
• Works on the principle of gas multiplication
• Can detect low energy X-rays, fast neutron, slow
neutrons or gamma rays
• Requires low voltage for working than GM counter
but higher than ionozation chamber
• Can detect uncharged particles
• Pulse height depends on energy of incident
radiation
• High resolution
• Useful to study Mossbauer effect also
98

99. Proportional counters
Voltage
-
- -
-- --
-
-
99

100. Scintillation counter
• A scintillation counter is an instrument for
detecting and measuring ionizing radiation by using
the excitation effect of incident radiation on a
scintillating material, and detecting the resultant
light pulses.
100

101. Scintillation counter
101

102. applications
Chemical
investigation
Physico-
chemical
applications
Analytical
applications
Age
determination
Medical
application
Agriculture
applications
Prospecting of
natural
resources
Industrial
applications
102

103. Chemical
investigations
Reaction
mechanism
•Structure
determinations
•Isotope
exchange
reactions
• Esterification, hydrolysis,
oxidation of H2O2, fumaric acid,
CO etc., Friedal Crafts’ reactions
• evidence for intermediates
• PCl5,
thiosulphate ion
103

104. Physico-
chemical
research
Solubility of
sparingly
soluble
compound
•Surface
area of a
powder or
precipitate
•Rates of
diffusion
Solubility of
sparingly
soluble
compound
104

105. Analytical
applications
radiochromato
graphy
•Isotope
dilution
analysis
•Isotope
exchange
reactions
Neutron
activation
analysis
Neutron
absorptiometry
Radiometric
titrations
•Isotope
dilution
analysis
Neutron
activation
analysis
NAA,
PGNAA
Neutron
absorptiom
etryRadiometri
c titrations
105

106. Age
determinations
Dating by
tritium content
•Dating by
carbon
Age of earth
Age of minerals
and rocks
106

107. Medical
applications
Volume of
blood
Defects in
blood
circullation
Mechanism of
bone fracture
healing
Study
neurotransmit
ter pathway in
brain
Other
application
radioimmunoa
ssay
Thyroiditis
Brain tumor
location
107