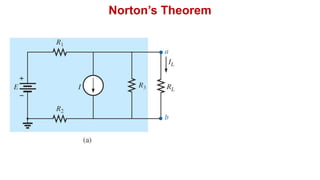
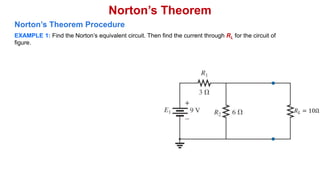
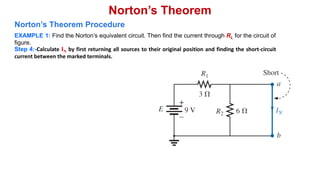
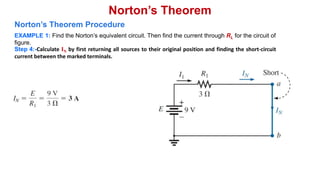
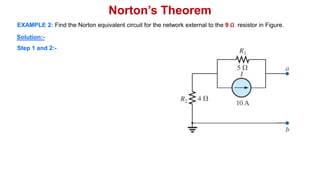
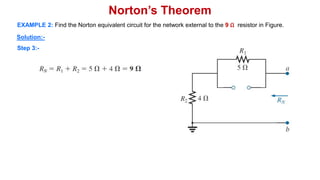
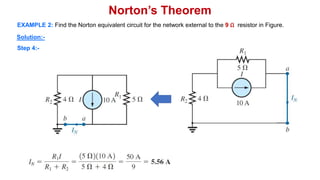
Norton's theorem states that a linear two-terminal circuit can be replaced by an equivalent circuit consisting of a current source (IN) in parallel with a resistor (RN), where IN is the short-circuit current and RN is the equivalent resistance when independent sources are turned off. The procedure for finding the Norton equivalent circuit involves removing the load, calculating the short-circuit current and equivalent resistance, and replacing the removed portion with the equivalent circuit. Once found, the Norton equivalent circuit can be used to calculate currents in other parts of the original circuit. Examples are provided to demonstrate finding the Norton equivalent circuit and using it to solve for currents.

1. ‫د‬
.
‫عبدهللا‬ ‫سليمان‬ ‫احمد‬
By Dr. Ahmed S. Abdullah
Norton’s Theorem
DC Circuits

2. Norton’s Theorem
Norton’s theorem states that a linear two-terminal circuit can be replaced by
an equivalent circuit consisting of a current source IN in parallel with a
resistor RN, where IN is the short-circuit current through the terminals and RN
is the input or equivalent resistance at the terminals when the independent
sources are turned off.

3. Norton’s Theorem

4. 𝑰𝑳 =
𝑰𝑵𝑹𝑵
𝑹𝑵 + 𝑹𝑳
Norton’s Theorem

5. Norton’s Theorem Procedure
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
𝑅𝐿 = 10Ω
Norton’s Theorem

6. Step 1:- Remove that portion of the network where the Norton’s equivalent circuit is found. In Figure
below, this requires that the load resistor RL be temporarily removed from the network.
𝑅𝐿 = 10Ω
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

7. Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Step 1:- Remove that portion of the network where the Norton’s equivalent circuit is found. In Figure
below, this requires that the load resistor RL be temporarily removed from the network.
Norton’s Theorem Procedure

8. Step 2:- Mark the terminals of the remaining two-terminal network. (The importance of this step will
become obvious as we progress through some complex networks.)
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

9. Step 3:-Calculate RN by first setting all sources to zero (voltage sources are replaced by short circuits, and
current sources by open circuits) and then finding the resultant resistance between the two
marked terminals.
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

10. Step 4:-Calculate IN by first returning all sources to their original position and finding the short-circuit
current between the marked terminals.
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

11. Step 4:-Calculate IN by first returning all sources to their original position and finding the short-circuit
current between the marked terminals.
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

12. Step 4:-Calculate IN by first returning all sources to their original position and finding the short-circuit
current between the marked terminals.
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

13. Step 4:-Calculate IN by first returning all sources to their original position and finding the short-circuit
current between the marked terminals.
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure

14. Step 5:-Draw the Norton’s equivalent circuit with the portion of the circuit previously removed replaced
between the terminals of the equivalent circuit.
Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Norton’s Theorem Procedure
𝑰𝑵 = 𝟑𝑨
𝑹𝑵 = 𝟐Ω
= 10Ω
𝑰𝑳 =
𝑰𝑵𝑹𝑵
𝑹𝑵 + 𝑹𝑳
=
(𝟑𝑨)(𝟐Ω)
𝟐Ω + 𝟏𝟎Ω
=
𝟔
𝟏𝟐
= 𝟎. 𝟓 𝑨

15. Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Converting the Norton equivalent circuit to a Thévenin equivalent circuit.

16. Norton’s Theorem
EXAMPLE 1: Find the Norton’s equivalent circuit. Then find the current through RL for the circuit of
figure.
Converting the Norton equivalent circuit to a Thévenin equivalent circuit.
𝑰𝑵 = 𝟑𝑨
𝑹𝑵 = 𝟐Ω
= 10Ω = 10Ω
= 𝑹𝑵= 𝟐Ω
𝑬𝑻𝒉 = 𝑰𝑵𝑹𝑵 = 𝟑𝑨 𝟐Ω = 𝟔𝑽
𝟔 𝑽

17. EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.
Norton’s Theorem

18. Step 1 and 2:-
Solution:-
Norton’s Theorem
EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.

19. Solution:-
Step 3:-
Norton’s Theorem
EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.

20. Solution:-
Step 4:-
Norton’s Theorem
EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.

21. Solution:-
Step 4:-
Norton’s Theorem
EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.

22. Solution:-
Step 4:-
Norton’s Theorem
EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.

23. Norton’s Theorem
𝑰𝑵 = 𝟓. 𝟓𝟔𝑨
𝑹𝑵 = 𝟗Ω
= 9Ω
𝑰𝑳 =
𝑰𝑵𝑹𝑵
𝑹𝑵 + 𝑹𝑳
=
(𝟓. 𝟓𝟔𝑨)(𝟗Ω)
𝟗Ω + 𝟗Ω
=
𝟓𝟎. 𝟎𝟒
𝟏𝟖
= 𝟐. 𝟕𝟖 𝑨
EXAMPLE 2: Find the Norton equivalent circuit for the network external to the 9 Ω resistor in Figure.
Solution:-
Step 5:-
Or 𝑰𝑳 =
𝑰𝑵
𝟐
=
𝟓. 𝟓𝟔𝑨
𝟐
== 𝟐. 𝟕𝟖 𝑨

24. References
 Boylestad, Robert L. Introductory circuit analysis. Pearson Education, 2010.
 Robbins, Allan H., and Wilhelm C. Miller. Circuit analysis: Theory and
practice. Cengage Learning, 2012.
 Sadiku, Matthew NO, and Chales K. Alexander. Fundamentals of electric
circuits. McGraw-Hill Higher Education, 2007.