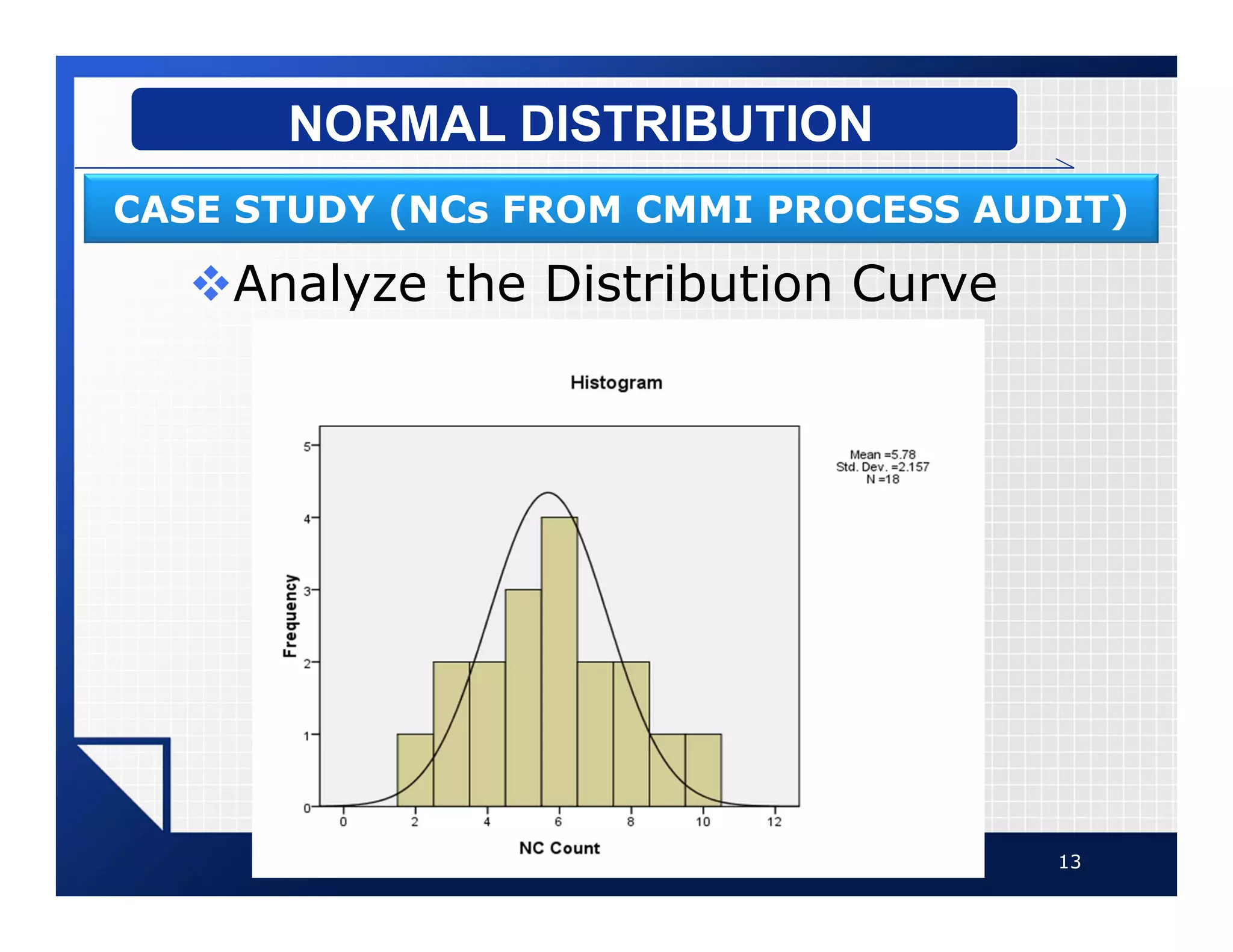
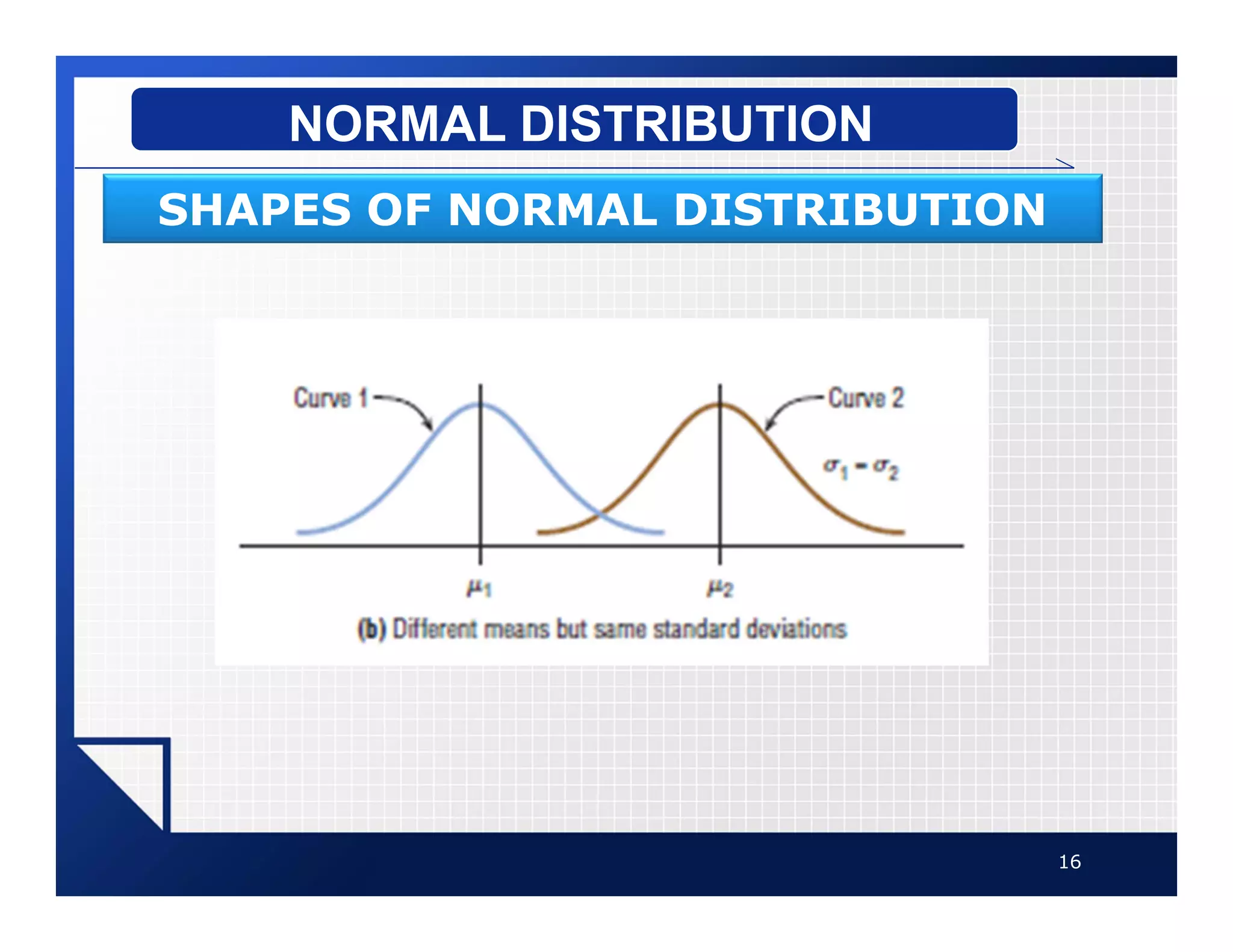
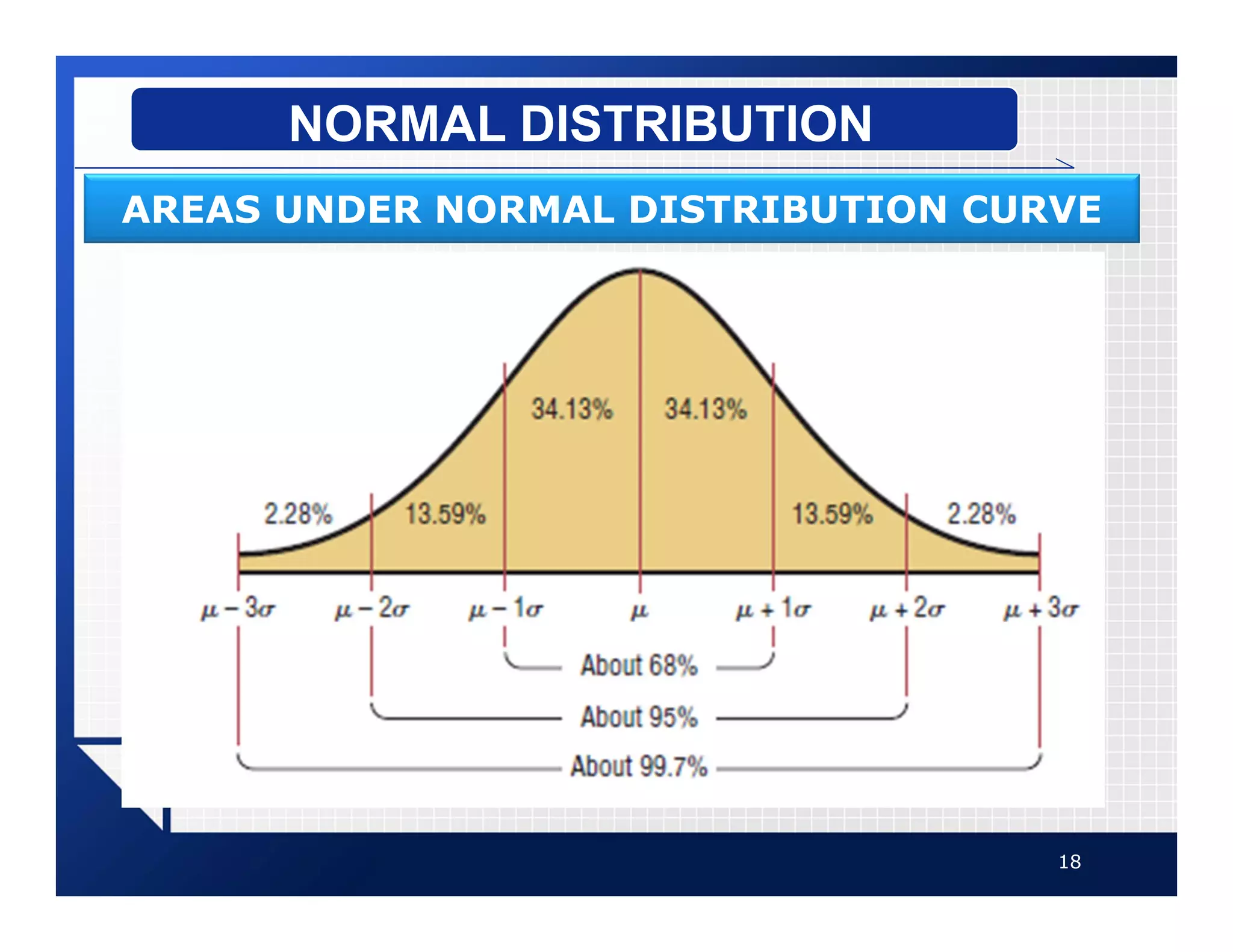
The document discusses normal distributions, which describe a continuous and symmetric bell-shaped distribution. A normal distribution is defined by its mean and standard deviation. It has several important properties including being symmetrical about the mean and having the mean, median and mode located at the center. As an example, the document analyzes non-conformances from a CMMI process audit, drawing a frequency distribution table and histogram to illustrate a normal distribution. It also discusses how the empirical rule can be used to determine the percentage of values that fall within a certain number of standard deviations from the mean.

1. Normal Distribution and its applications
1

2. 2
NORMAL DISTRIBUTIONS
1

3. ™When the data values are evenly
distributed about the mean, a
distribution is said to be a
Normal Distribution (symmetric
distribution).
™A normal distribution is a
continuous, symmetric, bell-
shaped distribution of a variable.
3
NORMAL DISTRIBUTION

4. 4
NORMAL DISTRIBUTION
™The area under a normal distribution
curve is used more often than the values
on the y axis. Therefore, when a normal
distribution is pictured, the y axis is
sometimes omitted

5. ™The mathematical equation for a
normal distribution is;
™Where
ƒ e = 2.718
ƒ = 3.14
ƒ µ = Population Mean
ƒ =Standard Deviation
5
NORMAL DISTRIBUTION
FORMULA

6. ™The shape and position of a
normal distribution curve
depend on two parameters;
ƒ Mean
ƒ Standard Deviation
6
NORMAL DISTRIBUTION
FORMULA

7. ™The curve is continuous.
™The curve is bell-shaped.
™The curve is symmetrical about
the mean.
™The mean, median and mode
are located at the center of the
distribution and are equal to
each other.
7
NORMAL DISTRIBUTION
IMPORTANT PROPERTIES

8. ™The curve never touches the x-
axis
™The total area under the normal
curve is equal to 1.
8
NORMAL DISTRIBUTION
IMPORTANT PROPERTIES

9. ™SEI Auditors have performed the
Class C appraisal of ‘Welcome
Technologies’ for CMMI Level 2,
3, 4 and 5 processes. They
found several NCs in 18 different
process areas. No. of NCs found
in 18 process areas are enlisted
below;
™3, 5, 3, 6, 4, 8, 10, 2, 6, 5, 7, 4,
9, 5, 6, 6, 8, 7
9
NORMAL DISTRIBUTION
CASE STUDY (NCs FROM CMMI PROCESS AUDIT)

10. ™Draw the Frequency Distribution
(Histogram) of given Data
™Analyze the Distribution Curve
10
NORMAL DISTRIBUTION
CASE STUDY (NCs FROM CMMI PROCESS AUDIT)

11. ™Draw the Frequency Distribution Table
11
NORMAL DISTRIBUTION
CASE STUDY (NCs FROM CMMI PROCESS AUDIT)
Classes X Frequency F(x)
2 1
3 2
4 2
5 3
6 4
7 2
8 2
9 1
10 1

12. ™Draw the Histogram
12
NORMAL DISTRIBUTION
CASE STUDY (NCs FROM CMMI PROCESS AUDIT)

13. ™Analyze the Distribution Curve
13
NORMAL DISTRIBUTION
CASE STUDY (NCs FROM CMMI PROCESS AUDIT)

14. ™Demo with SPSS
14
NORMAL DISTRIBUTION
CASE STUDY (NCs FROM CMMI PROCESS AUDIT)

15. 15
NORMAL DISTRIBUTION
SHAPES OF NORMAL DISTRIBUTION

16. 16
NORMAL DISTRIBUTION
SHAPES OF NORMAL DISTRIBUTION

17. 17
NORMAL DISTRIBUTION
SHAPES OF NORMAL DISTRIBUTION

18. 18
NORMAL DISTRIBUTION
AREAS UNDER NORMAL DISTRIBUTION CURVE

19. ™Empirical Rule: (Also called 68-95-
99.7 rule or three sigma rule)
ƒ About 68.27% of the values lie within 1
standard deviation of the mean
ƒ About 95.45% of the values lie within 2
standard deviations of the mean
ƒ About 99.73% of the values lie within 3
standard deviation of the mean
19
NORMAL DISTRIBUTION
AREAS UNDER NORMAL DISTRIBUTION CURVE