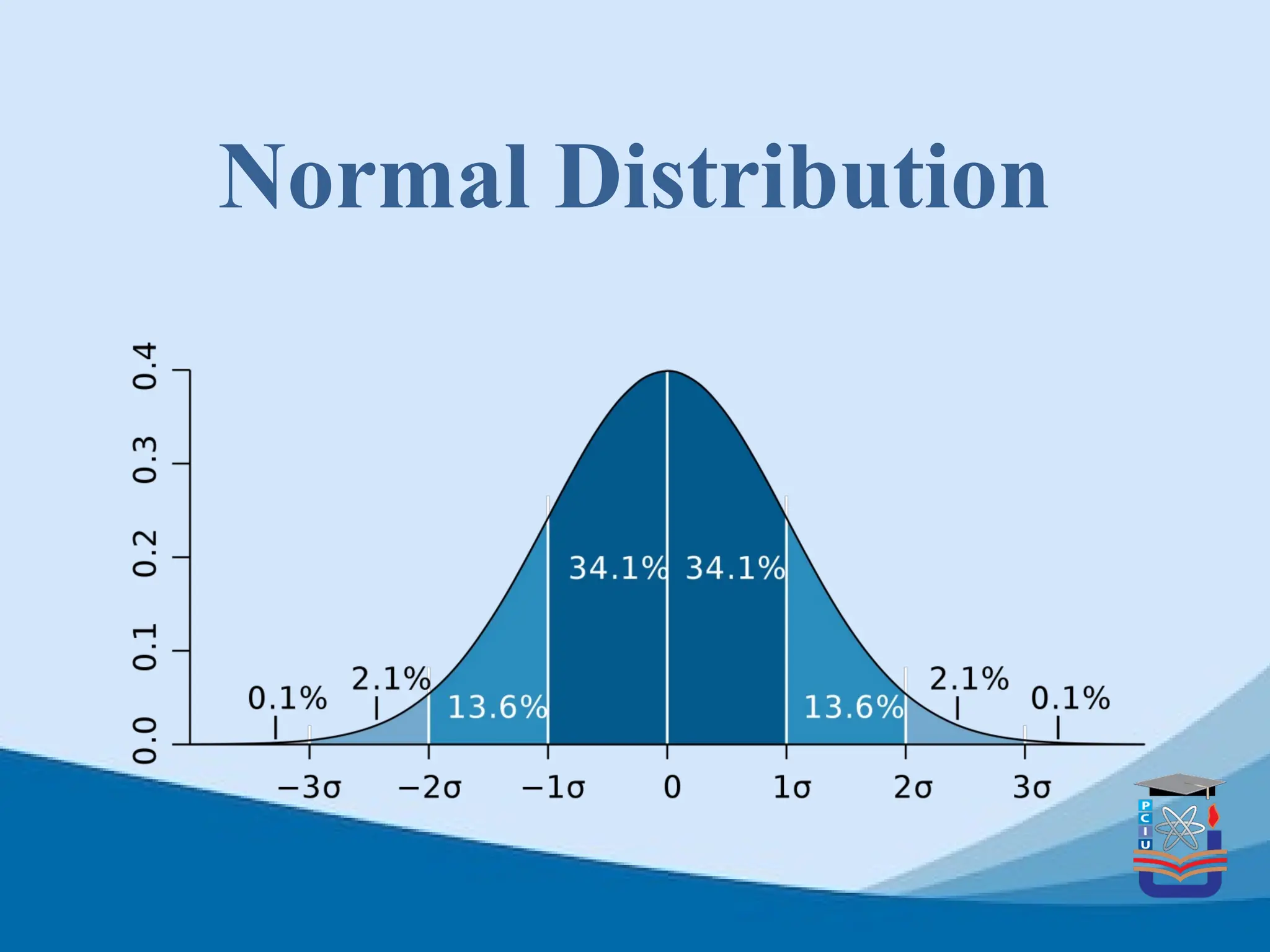
The document provides an overview of normal distribution, defining it as a continuous probability distribution characterized by its mean and variance. It discusses the historical background, applications in various fields such as statistics, finance, and computer science, and outlines its key characteristics, such as symmetry and the bell-shaped curve. The conclusion emphasizes the appropriate use of normal distribution in analyzing continuous, symmetric, and bell-shaped data while cautioning against its use in skewed or multimodal datasets.

1. Normal Distribution

2. Topic: Normal Distribution
Submitted to: Submitted by:
Md. Ashraful Islam
Lecturer
Department of Natural Science
Indrajith Goswami
Batch: CSE 31 Evening
Id: CSE 031 08143

3. Definition
A continuous random variable X is said to have a normal distribution if
its probability density function is defined by
Here and e are mathematical contents. and are two parameters of the
distribution. is mean and is the variance of the distribution.

4. History
Normal Distribution is a continuous
probability distribution. It is a very important
distribution in statistics. The normal
distribution was discovered by a French
mathematician De-Moivre as the limiting
case of binomial distribution in 1733. The
other eminent mathematicians were Laplace
and Gauss who played important role in its
development. In honor of the important
contribution of Gauss, the normal distribution
is often call the Gaussian distribution. The
distribution of heights, weights, and errors
made in measuring certain physical quantities.

5. Examples of Normal
Distribution
Human Height: The distribution of human height in a population typically
follows a normal curve, with most people near the average height.
IQ Scores: IQ scores are designed to follow a normal distribution, with the
majority of people scoring near the average of 100.
Measurement Errors: Small random errors in measurements often follow
a normal distribution, with most errors being close to zero.
Blood Pressure: Systolic blood pressure in a healthy population often
forms a normal distribution, with most individuals near the average.
Test Scores: Standardized test scores, like SATs, follow a normal
distribution, with most students scoring around the average.
Weight of Produce: The weight of produce, such as apples, often follows a
normal distribution, with most items around the average weight.
Employee Salaries: Employee salaries in a company often approximate a
normal distribution, with most salaries near the average.

6. Characteristics of Normal Distribution
Symmetry: The normal distribution is perfectly symmetrical around its mean,
so the left and right sides of the distribution are identical.
Bell-shaped Curve: The graph of the normal distribution forms a bell-shaped
curve, with the peak at the mean (μ).
Mean, Median, Mode: In a normal distribution, the mean, median, and mode
are all equal and occur at the center of the distribution.
Asymptotic Tails: The tails of the distribution approach but never actually
touch the horizontal axis, implying that extreme values are possible but rare.
Defined by Two Parameters:
Mean (μ): The center of the distribution.
Standard deviation (σ): The spread or width of the distribution. Larger
values
of σ result in a wider curve, and smaller values result in a narrower curve.

7. Applications of Normal Distribution
Statistical Inference: It is used to make predictions and inferences about a
population based on sample data. Techniques like confidence intervals and
hypothesis testing often assume data is normally distributed.
Quality Control: In manufacturing, many processes assume that defects or
variations follow a normal distribution, allowing companies to monitor quality and
make adjustments.
Finance: Stock prices, returns, and other financial variables often assume normality
(though real-world financial data may exhibit "fat tails"). Risk management models
like Value at Risk (VaR) often assume normal distributions.
Psychometrics: Tests like IQ tests are designed to produce scores that follow a
normal distribution, helping to measure and categorize human intelligence.

8. Why We Use the Normal Distribution?
Simplicity: The normal distribution is mathematically tractable, meaning it is easy to
calculate probabilities, make predictions, and perform statistical tests.
Central Limit Theorem: Even if the data isn't normally distributed, the distribution
of the sample mean will tend to be normal when the sample size is sufficiently large
(usually greater than 30).
Natural Occurrence: Many natural and human-made phenomena tend to follow a
normal distribution, making it a good model for real-world data.

9. Application of Normal Distribution in
Computer Science
Machine Learning and Data Science: In supervised learning, the assumption of
normality often helps with feature scaling, outlier detection, and other preprocessing
steps. Gaussian Naive Bayes is a classification algorithm that assumes the features are
normally distributed within each class.
Random Number Generation: Normal distributions are often used to generate random
numbers for simulations or Monte Carlo methods. For example, Gaussian noise is
frequently used in simulations, image processing, and machine learning algorithms.
Data Compression: In algorithms like Huffman coding, normal distributions can help
identify which data values are most likely, allowing for more efficient encoding.
Signal Processing: In filtering and noise reduction, Gaussian filters are used because
they model random noise in many systems.

10. Conclusion
We use the normal distribution when the data is continuous, symmetric, and bell-
shaped, and when sample sizes are large enough for the Central Limit Theorem to
apply. It is also the go-to model for statistical tests and for analyzing phenomena
where the data results from many independent factors. However, if the data is
skewed, multimodal, or has heavy tails, the normal distribution may not be
appropriate, and other statistical models should be considered. Understanding
these conditions ensures that we apply the normal distribution in the right context,
leading to more accurate analysis and conclusions.

11. Thank You