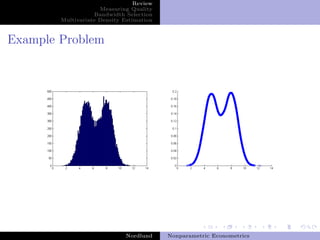
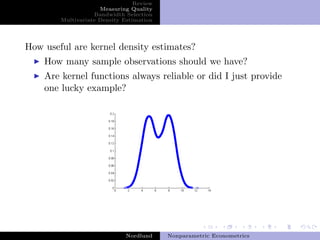
This document summarizes key concepts in nonparametric econometrics and kernel density estimation. It discusses bandwidth selection methods like cross-validation and plug-in approaches. It also covers multivariate density estimation, noting the trade-off between bias and variance. The document analyzes a real example from DiNardo and Tobias on estimating the density of female wages.



![Review
Measuring Quality
Bandwidth Selection
Multivariate Density Estimation
Definitions
Definition (Convergence in rth Mean)
We say that xn converges to X in the rth mean, if for some
r > 0,
lim E[||xn − X||r ] = 0
n→∞
rth
We write this as xn → X
Nordlund Nonparametric Econometrics](https://image.slidesharecdn.com/npdnordlund-13058405051495-phpapp02-110519162856-phpapp02/85/Nonparametric-Density-Estimation-6-320.jpg)


![Review
Measuring Quality
Bandwidth Selection
Multivariate Density Estimation
Inside the Proof
Recall that
ˆ ˆ ˆ ˆ
M SE(f (x) = E [f (x) − f (x)]2 = V ar(f (x)) + Bias(f (x))2 .
Along the proof, we obtain
ˆ h2 (2)
Bias(f (x)) = f (x) u2 k(u)du + O(h3 )
2
and
ˆ 1
V ar(f (x)) = f (x) k(u)j du + O(h)
nh
Notice that there is a trade off between minimizing variance
and bias
Nordlund Nonparametric Econometrics](https://image.slidesharecdn.com/npdnordlund-13058405051495-phpapp02-110519162856-phpapp02/85/Nonparametric-Density-Estimation-9-320.jpg)











